Unity中实现滑块跟随物体的算法解析

Unity制作滑块跟随物体教程：直线与平面跟随效果实现方法

在Unity中制作一个能够跟随物体移动的滑块，不仅可以增强游戏的互动性，还可以用于各种动态UI元素的制作。本文将详细介绍如何实现滑块在不同轨迹上的跟随效果。

效果示意图

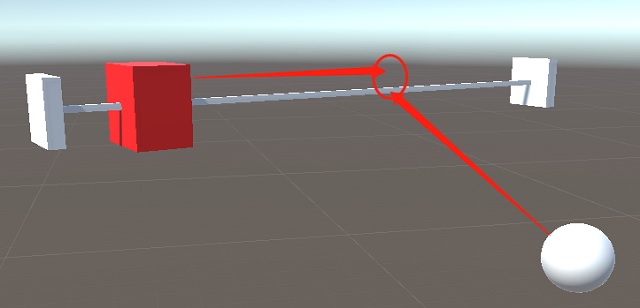
制作一个能够跟随物体的滑块

需求分析

我们希望滑块能够严格跟随一个球体移动，同时自身被限制在特定的轨道上。滑块不能离开轨道，且需要实时跟随球体的位置。这可以通过数学算法来实现，类似于在已知三个点A、B、C的坐标下，求解C点垂直于AB线段的坐标。

解决方案1

算法实现

直线上的跟随

假设mAPoint是起始点，mBPoint是结束点，mCurrentPoint是当前移动的点，我们需要返回映射的点。首先，我们计算AB两点的向量：

Vector3 vectorAB = mBPoint - mAPoint;

接下来，计算点积和向量的长度平方：

float dotProduct = Vector3.Dot(vectorAB, mCurrentPoint - mAPoint);
float lengthSquared = vectorAB.sqrMagnitude;

然后，限制点积的范围，确保映射点在AB线段上：

dotProduct = Mathf.Clamp(dotProduct, 0f, lengthSquared);

最后，计算映射点的位置：

Vector3 PointA = mAPoint + vectorAB * dotProduct / lengthSquared;
Vector3 PointB = mCurrentPoint + (PointA - mCurrentPoint);
return PointB;

平面上的跟随

假设mNormal是平面的法线方向，mTargetPoint是平面上的位置点，mCurrentPoint是当前移动的点。我们可以使用向量的投影来实现在平面上的跟随效果：

Vector3 projection = mCurrentPoint - Vector3.Dot(mCurrentPoint - mTargetPoint, mNormal) * mNormal;

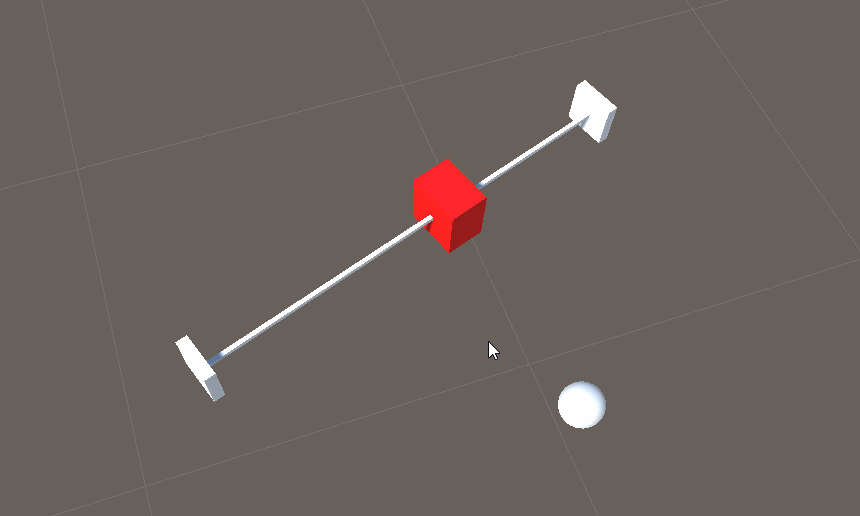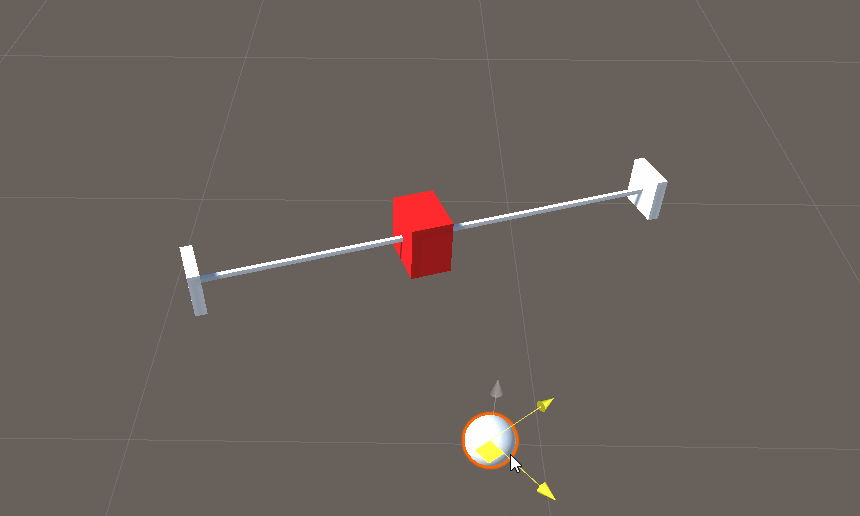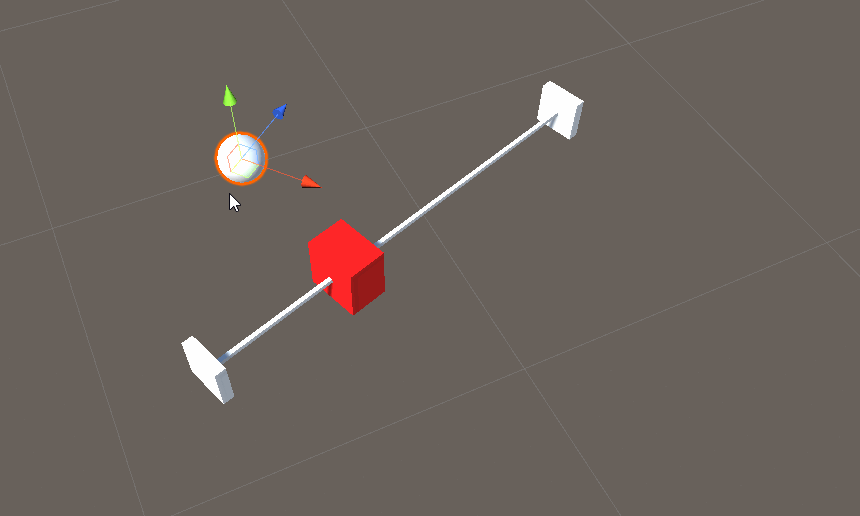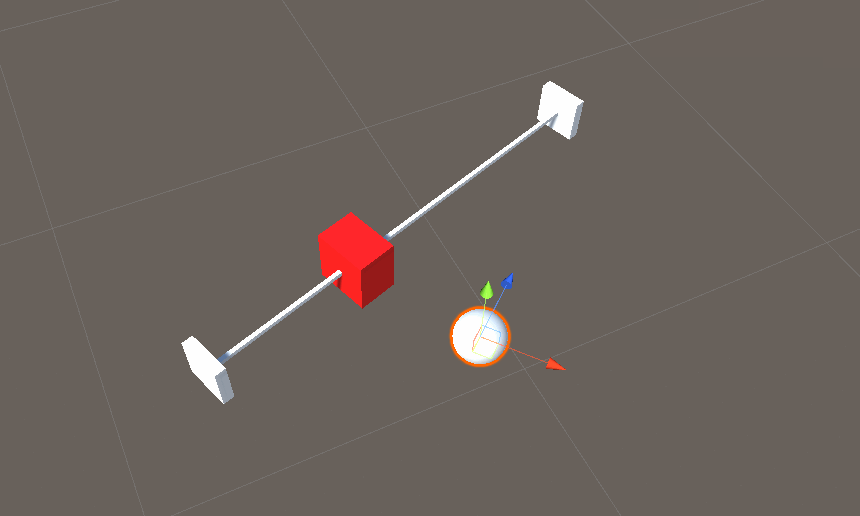
实现效果

通过以上算法，我们成功实现了滑块在直线和平面上的跟随效果！这使得在制作游戏中的轨道或者其他需要物体跟随的情景中更加容易实现。

实现的最终效果示意图

解决方案2

算法实现：

直线轨道上的滑块跟随：

首先确定起始点mAPoint和结束点mBPoint。

计算AB两点的向量： $Vector3 vectorAB = mBPoint - mAPoint;$ Vector3 vectorAB=mBPoint−mAPoint;

计算当前点mCurrentPoint与A点的相对向量，并与AB向量计算点积，以及AB向量的模的平方。

通过点积与模的平方比值，限制mCurrentPoint在AB线段上的位置，防止超出轨道。

最终映射计算出滑块的新位置。

曲线轨道上的滑块跟随：

类似于直线轨道，但需要考虑曲线的参数化表示，可能需要引入额外的数学工具，如贝塞尔曲线等。

面上的滑块跟随：

需要一个法向量mNormal来确定滑块在面上的移动方向。

通过投影计算，确保滑块在目标点mTargetPoint的法线上移动

代码示例

以下是Unity中实现直线轨道上滑块跟随的示例代码：

Vector3 vectorAB = mBPoint - mAPoint;
float dotProduct = Vector3.Dot(vectorAB, mCurrentPoint - mAPoint);
float lengthSquared = vectorAB.sqrMagnitude;

if (dotProduct > lengthSquared) dotProduct = lengthSquared;
if (dotProduct < 0) dotProduct = 0;

Vector3 PointA = mAPoint + vectorAB * (dotProduct / lengthSquared);
Vector3 PointB = mCurrentPoint + (PointA - mCurrentPoint);
return PointB;