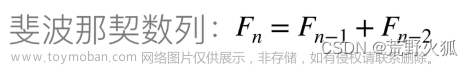数据结构与算法之动态规划: Leetcode 509. 斐波那契数 (Typescript版)

这篇具有很好参考价值的文章主要介绍了数据结构与算法之动态规划: Leetcode 509. 斐波那契数 (Typescript版)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

斐波那契数

https://leetcode.cn/problems/fibonacci-number/

描述

斐波那契数（通常用 F(n) 表示）形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：
```
F(0) = 0，F(1) = 1
F(n) = F(n - 1) + F(n - 2)，其中 n > 1
```
给定 n ，请计算 F(n) 。

示例 1

输入：n = 2
输出：1
解释：F(2) = F(1) + F(0) = 1 + 0 = 1

示例 2

输入：n = 3
输出：2
解释：F(3) = F(2) + F(1) = 1 + 1 = 2

示例 3

输入：n = 4
输出：3
解释：F(4) = F(3) + F(2) = 2 + 1 = 3

提示

0 <= n <= 30

算法实现

1 ）方案 1

function fib(n: number): number {
    if (n === 0) return 0
    if (n === 1) return 1
    return fib(n-1) + fib(n-2)
}

这种是递归, 性能非常不好, 当n大了的时候，性能会急剧下降

2 ）方案 2

function fib(n: number): number {
    let fibs: number[] = [0,1];
    for(let i: number = 2; i <= n; i++){
        fibs[i] = fibs[i-1] + fibs[i-2];
    }
    return fibs[n];
};

思路：
- 0, 1, 后面任何一个数字，就是其前两个的和
- 定义子问题：F(n) = F(n-1) + F(n-2)
- 反复执行：从2循环到n,执行上述公式

3 ）方案 3文章来源地址https://www.toymoban.com/news/detail-443247.html

function fib(n: number): number {
    if (n === 0) return 0
    if (n === 1) return 1
    let start:number = 0
    let end:number = 1
    for(let i: number = 2; i <= n; i++) {
        const endTmp:number = end
        end += start
        start = endTmp
    }
    return end;
};