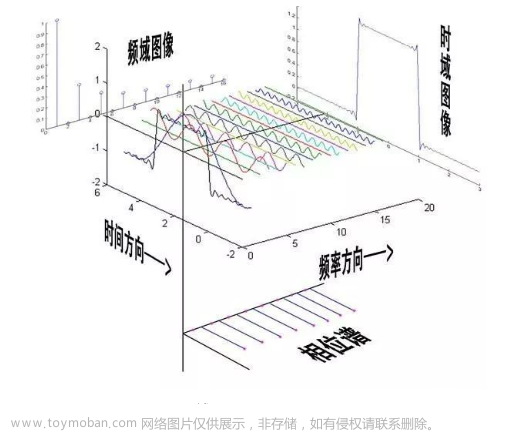
OpenCV图像处理之傅里叶变换

这篇具有很好参考价值的文章主要介绍了OpenCV图像处理之傅里叶变换。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

OpenCV图像处理之傅里叶变换

傅里叶变换：目的就是得到图像的低频和高频，然后针对低频和高频进行不同的处理。处理完之后，在通过逆变换恢复到图像，这时候对低频和高频的处理就会反映到图像上。

频率

高频：变化剧烈的灰度分量，例如边界。
低频：变化缓慢的灰度分量，例如一天蓝天(相似的多)。

滤波

低通滤波器：只保留低频，会使图像模糊。
高通滤波器：只保留高频，会使图像细节增强。

图像处理之傅里叶变换流程图

OpenCV图像处理之傅里叶变换

OpenCV主要就是cv.dft()和cv.idft(),输入图像需要先转换成np.float32格式,得到的结果中频率为0,的部分会在左上角，通常要转换到中心位置，可以通过shift变换来实现, cv.dft()返回的结果是双通道的(实部、虚部)，通常需要转换成图像格式才能展示（0,255）

OpenCv图像处理之傅里叶变换

# 读取一张灰度图像
img = cv.imread('img/tree.jpg',0)
# 将图像转换成np.float32格式
img_float32 = np.float32(img)
# cv.dft()函数进行傅里叶变换，返回的结果是双通道的(实部、虚部)，通常需要转换成图像格式才能展示（0,255）
dft = cv.dft(img_float32, flags = cv.DFT_COMPLEX_OUTPUT)
# 再调用 np.fft.fftshift() 函数将中心位置转移至中间。
dft_shift = np.fft.fftshift(dft)
# cv.magnitude()是OpenCV中的一个函数，用于计算两个数组的逐元素欧几里得距离。
# 具体来说，该函数可以计算两个数组（可以是实数或复数数组）的逐元素欧几里得距离，返回一个与输入数组形状相同的数组。
# 得到灰度图能表示的形式(转换成图像格式才能展示（0,255）)，映射公式，需要将像素值映射之0-255
magnitude_spectrum = 20*np.log(cv.magnitude(dft_shift[:,:,0],dft_shift[:,:,1]))
# 傅里叶变换后图像进行展示
plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(magnitude_spectrum, cmap = 'gray')
plt.title('OpenCV Magnitude Spectrum'), plt.xticks([]), plt.yticks([])
plt.show()

OpenCV图像处理之傅里叶变换

获取图像的中心位置

rows, cols = img.shape
crow, ccol = int(rows/2) , int(cols/2) # 中心位置

OpenCv傅里叶变换之低通滤波

# 设置遮掩的形状(一般为矩形、圆形)，大小(自定义)
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-50:crow+50, ccol-50:ccol+50] = 1

# IDFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv.idft(f_ishift)
img_back = cv.magnitude(img_back[:,:,0],img_back[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Result'), plt.xticks([]), plt.yticks([])
plt.show()

OpenCV图像处理之傅里叶变换

OpenCv傅里叶变换之高通滤波

# 设置遮掩的形状(一般为矩形、圆形)，大小(自定义)
mask = np.ones((rows, cols, 2), np.uint8)
mask[crow-5:crow+5, ccol-5:ccol+5] = 0

# IDFT
fshift = dft_shift*mask
f_ishift = np.fft.ifftshift(fshift)
img_back = cv.idft(f_ishift)
img_back = cv.magnitude(img_back[:,:,0],img_back[:,:,1])

plt.subplot(121),plt.imshow(img, cmap = 'gray')
plt.title('Input Image'), plt.xticks([]), plt.yticks([])
plt.subplot(122),plt.imshow(img_back, cmap = 'gray')
plt.title('Result'), plt.xticks([]), plt.yticks([])

plt.show()

OpenCV图像处理之傅里叶变换

大家可以更改mask的大小或形状对图像进行处理，对比着学习起来更容易理解。

# 设置遮掩的形状(一般为矩形、圆形)，大小(自定义)
mask = np.zeros((rows, cols, 2), np.uint8)
mask[crow-30:crow+30, ccol-30:ccol+30] = 1

在这里给大家推荐几个关于傅里叶变换的学习网页以及视频。
哔站：B站首发！草履虫都能看懂的【傅里叶变换】讲解，清华大学李永乐老师教你如何理解傅里叶变换，辨清美颜和变声原理，！！
傅里叶变换这样学，何愁不会呢？直观理解傅里叶变换
图像傅里叶变换实验文章来源地址https://www.toymoban.com/news/detail-461228.html

到了这里，关于OpenCV图像处理之傅里叶变换的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！