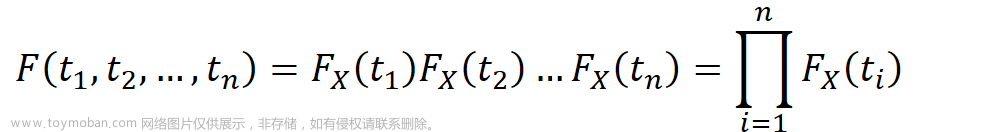1.1.1随机试验与随机事件
统计规律
1.随机试验(用E表示):
(1)在相同条件下可重复
(2)结果不止一个
(3)无法预测
2.事件:每种试验结果
3.随机事件(用大写A,B,C……表示):可能发生也可能不发生的时间
4.基本事件:相对于试验目的不可再分(不必再分)
5.复合事件:由基本事件复合
6.全集(样本空间):Ω(空集:φ)
7.必然事件(Ω(大写欧米伽)):每次试验必然发生的事件(不随机)
8.不可能事件(φ(fai)):一定不发生的事件(不随机)

1.1.2样本空间与事件集合表示
1.样本空间:所有基本事件的集合
2.样本点(ω(小写欧米伽)):样本空间中的元素(其实就是基本事件)
例如:扔硬币:Ω={正,反}
投行骰子:Ω={1,2,3,4,5,6}
电话被打的次数:Ω={1,2,3,4,5,6……n……}
3.事件集合的表示:A={2,3,4} B={1,2}
4. Ω——必然事件——样本空间
φ——不可能事件——空集
1.1.3事件间的关系
1.包含关系:A发生必然导致B发生
包含关系: ∅⊂A⊂Ω

2.相等关系
:A包含于B,B也包含于A
3.并关系 (A∪B /A+B):A和B至少有一个发生
4.交关系 (A∩B=AB):A和B同时发生
5.无限可列个:按某种规律排成一个序列
例如:(1)自然数:0,1,2,3,4,5,6……(2)整数:0,1,-1,2,-2,3,-3……(3)有理数:p/q,0,1/1,-1/1,1/2,-1/2……
6.差关系 : (A−B) A发生而B不发生, A−B=A−AB
7.互不相容事件 :(A∩B=∅):A和B不同时发生,也就是他们的交集是空集
8.对立事件( A+B=Ω 并且 A∩B=∅):A和B并不相容并且A+B=Ω也叫

(A等于B的逆)或者反过来写A上划横线,叫做B等于A 的逆

互不相容事件与对立事件的联系和区别:
(1)两个事件对立,一定是互不相容的
(2)互不相容适用于多个事件,对立只适用于两个事件
(3)互不相容事件不能同时发生,也可以都不发生。对立事件有且只有一个发生

9.完备事件组 :A1,A2,⋅⋅⋅,An,两两互不相容,又能组成全集


运算律
1.交换律
(1)A∩B=B∩A
(2)A∪B=B∪A
2.结合律
(1)(A∩B)∩C=A∩(B∩C)
(2)(A∪B)∪C=A∪(B∪C)
3.分配律
(1)(A∪B)∩C=(A∩C)∪(B∩C)
(2)(A∩B)∪C=(A∪C)∩(B∪C)
4.对欧律

例题:


本文章是宋浩老师的概率论与数理统计课程的笔记,为前3p内容所对应的笔记

视频链接:1.1.1 随机试验与随机事件【板书】_哔哩哔哩_bilibili
视频链接:1.1.2 样本空间与事件的集合表示【板书】_哔哩哔哩_bilibili文章来源:https://www.toymoban.com/news/detail-480079.html
视频链接:1.1.3 事件间的关系【板书】_哔哩哔哩_bilibili文章来源地址https://www.toymoban.com/news/detail-480079.html
到了这里,关于样本空间与事件集合,事件间的关系——概率论与数理统计(宋浩)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!