吴恩达471机器学习入门课程2第2周——手写数字识别（0到9）

使用神经网络来识别手写数字0-9。

1、导包

import numpy as np
import tensorflow as tf
from keras.models import Sequential
from keras.layers import Dense
from keras.activations import linear, relu, sigmoid
%matplotlib widget
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')

import logging
logging.getLogger("tensorflow").setLevel(logging.ERROR)
tf.autograph.set_verbosity(0)

from public_tests import *

from autils import *
from lab_utils_softmax import plt_softmax
np.set_printoptions(precision=2)

2、ReLU激活函数

本周，引入了一种新的激活函数，即修正线性单元（ReLU）。
$$a=max(0,z)\text{ ReLU函数}$$

plt_act_trio()

讲座中的例子展示了ReLU的应用。在这个例子中，上下文感知能力不是二进制的，而是具有连续的值范围。Sigmoid函数最适合开/关或二进制情况。ReLU提供了连续线性关系，并且还具有一个输出为零的“关闭”范围。
“关闭”功能使ReLU成为非线性激活函数。为什么需要这样做呢？这样可以使多个单元对结果函数做出贡献而不会相互干扰。这在支持性可选实验室中进行了更详细的探讨。

3 - Softmax函数

多类神经网络会生成N个输出。其中一个输出被选为预测答案。在输出层，通过线性函数生成向量$\mathbf{z}$，该向量被输入到softmax函数中。softmax函数将$\mathbf{z}$转换为概率分布，具体如下所述。应用softmax后，每个输出值都介于0和1之间，并且所有输出的和为1。它们可以被解释为概率。较大的softmax输入对应于较大的输出概率。

softmax函数的公式如下：
$$a_j=\frac{e^{z_j}}{{\sum }_{k=0}^{N-1}{e}^{z_k}}\text{\hspace{1em}(1)}$$

其中，$z=\mathbf{w}\cdot \mathbf{x}+b$，N是输出层中特征/类别的数量。

4 - 神经网络

在上周.实现了一个用于二元分类的神经网络。本周，您将扩展多类分类。这将利用softmax激活。

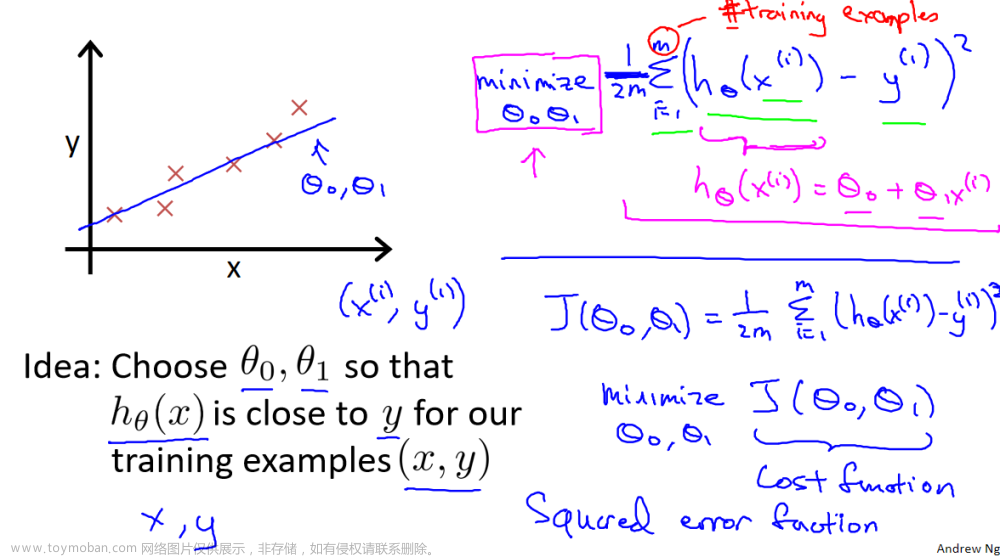
4.1 问题陈述

使用神经网络识别十个手写数字0-9。这是一个多类分类任务，其中选择n个选择之一。自动手写数字识别今天被广泛使用-从识别邮件信封上的邮政编码到识别银行支票上写的金额。

4.2 数据集

您将首先加载此任务的数据集。

• 下面显示的load_data()函数将数据加载到变量X和y中

• 数据集包含5000个手写数字的训练示例${}^1$。

  • 每个训练示例都是数字的20像素x20像素灰度图像。
    • 每个像素由浮点数表示，指示该位置处的灰度强度。
    • 20x20像素网格“展开”为400维向量。
    • 每个训练示例成为我们的数据矩阵X中的单个行。
    • 这给出了一个5000 x 400矩阵X，其中每行都是手写数字图像的训练示例。

X = ( − − − ( x ( 1 ) ) − − − − − − ( x ( 2 ) ) − − − ⋮ − − − ( x ( m ) ) − − − ) X = \left(\begin{array}{cc} --- (x^{(1)}) --- \\ --- (x^{(2)}) --- \\ \vdots \\ --- (x^{(m)}) --- \end{array}\right) X= ​−−−(x(1))−−−−−−(x(2))−−−⋮−−−(x(m))−−−​ ​

• 训练集的第二部分是一个5000 x 1维向量y，其中包含训练集的标签
  • 如果图像是数字’0’，则’y = 0’，如果图像是数字“4”，则’y = 4’，依此类推。

ReLu输出线性，sigmoid：0和1，softmax:将输出转换为概率

x,y = load_data()

4.2.1 可视化数据

您将从可视化训练集的子集开始。

• 在下面的单元格中，代码会随机选择X中的64行，将每行映射回一个20像素乘20像素的灰度图像，并将图像一起显示。
• 每个图像的标签显示在图像上方。

import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
m, n = x.shape

fig, axes = plt.subplots(8,8, figsize=(5,5))
fig.tight_layout(pad=0.13,rect=[0, 0.03, 1, 0.91]) #[left, bottom, right, top]

widgvis(fig)
for i,ax in enumerate(axes.flat):

    random_index = np.random.randint(m)


    x_random_reshaped = x[random_index].reshape((20,20)).T


    ax.imshow(x_random_reshaped, cmap='gray')


    ax.set_title(y[random_index,0])
    ax.set_axis_off()
    fig.suptitle("Label, image", fontsize=14)

4.3 模型表示

在本次任务中，使用下面的神经网络。

• 它具有两个带有ReLU激活函数的稠密层，后面跟着一个线性激活的输出层。
  • 回想一下，我们的输入是数字图像的像素值。
  • 由于图像的大小为$20\times 20$，因此这给了我们$400$个输入。

• 这些参数的维度大小适用于一个具有$25$个单元的第一层，$15$个单元的第二层和$10$个输出单元的第三层神经网络，每个数字对应一个输出单元。

  • 请记住，这些参数的维度是按照以下方式确定的：

    • 如果网络在一层中具有$s_{in}$个单元，在下一层中具有$s_{out}$个单元，则
      • $W$的维度为$s_{in}\times s_{out}$。
      • $b$将是一个具有$s_{out}$个元素的向量

  • 因此，W和b的形状为：

    • 第1层：W1的形状为(400, 25)，b1的形状为(25,)
    • 第2层：W2的形状为(25, 15)，b2的形状为(15,)
    • 第3层：W3的形状为(15, 10)，b3的形状为(10,)。

注意： 偏置向量b可以表示为1-D(n,)或2-D(n,1)数组。 Tensorflow使用1-D表示法，本实验室将保持这种约定：

tf.random.set_seed(1234)
model = Sequential(
    [
        tf.keras.layers.InputLayer((400,)),
        tf.keras.layers.Dense(25,activation='relu',name='l1'),
        tf.keras.layers.Dense(15,activation='relu',name='l2'),
        tf.keras.layers.Dense(10,activation='linear',name='l3'),
    ],name='my_model'
)

model.summary()

Model: "my_model"
_________________________________________________________________
 Layer (type)                Output Shape              Param #   
=================================================================
 l1 (Dense)                  (None, 25)                10025     
                                                                 
 l2 (Dense)                  (None, 15)                390       
                                                                 
 l3 (Dense)                  (None, 10)                160       
                                                                 
=================================================================
Total params: 10,575
Trainable params: 10,575
Non-trainable params: 0
_________________________________________________________________

model.compile(
    loss= tf.keras.losses.SparseCategoricalCrossentropy(from_logits=True),
    optimizer=tf.keras.optimizers.Adam(learning_rate=0.01)
)
his = model.fit(
    x,y,
    epochs=40
)

Epoch 1/40
157/157 [==============================] - 1s 2ms/step - loss: 0.6965
Epoch 2/40
157/157 [==============================] - 0s 2ms/step - loss: 0.3025
Epoch 3/40
157/157 [==============================] - 0s 2ms/step - loss: 0.2598
Epoch 4/40
157/157 [==============================] - 0s 2ms/step - loss: 0.1980
Epoch 5/40
157/157 [==============================] - 0s 2ms/step - loss: 0.1681
Epoch 6/40
157/157 [==============================] - 0s 2ms/step - loss: 0.1502
Epoch 7/40
157/157 [==============================] - 0s 2ms/step - loss: 0.1371
Epoch 8/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0978
Epoch 9/40
157/157 [==============================] - 0s 2ms/step - loss: 0.1206
Epoch 10/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0996
Epoch 11/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0879
Epoch 12/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0808
Epoch 13/40
157/157 [==============================] - 0s 3ms/step - loss: 0.1061
Epoch 14/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0938
Epoch 15/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0672
Epoch 16/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0754
Epoch 17/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0672
Epoch 18/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0595
Epoch 19/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0591
Epoch 20/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0537
Epoch 21/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0417
Epoch 22/40
157/157 [==============================] - 0s 2ms/step - loss: 0.1098
Epoch 23/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0692
Epoch 24/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0687
Epoch 25/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0554
Epoch 26/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0511
Epoch 27/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0680
Epoch 28/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0751
Epoch 29/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0499
Epoch 30/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0580
Epoch 31/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0231
Epoch 32/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0269
Epoch 33/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0566
Epoch 34/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0513
Epoch 35/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0269
Epoch 36/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0701
Epoch 37/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0504
Epoch 38/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0603
Epoch 39/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0189
Epoch 40/40
157/157 [==============================] - 0s 2ms/step - loss: 0.0282

批次和周期

在上面的compile语句中，epochs的数量设置为100。这指定整个数据集应在训练期间应用100次。在训练过程中，您将看到描述训练进度的输出，如下所示：

Epoch 1/100
157/157 [==============================]

• 0s 1ms/step - loss: 2.2770
  第一行“Epoch 1/100”描述了模型当前运行的时期。为了效率，训练数据集被分成“批次”。Tensorflow中默认的批量大小为32。我们的数据集中有5000个示例，或大约157个批次。第二行的符号“157/157 [====”描述已执行哪个批次。

损失 (cost)

在第一门课程中，我们学习了通过监控损失来跟踪梯度下降的进展。理想情况下，随着算法迭代次数的增加，损失应该减少。Tensorflow 将损失称为 loss。如上所述，在执行 model.fit 时，您会看到每个 epoch 显示的损失。.fit 方法返回多种指标，包括损失。这可以在上面的 history 变量中捕获。可以使用它来绘制下面所示的损失图表。

def plot_loss_tf(history):
    fig,ax = plt.subplots(1,1, figsize = (4,3))
    widgvis(fig)
    ax.plot(history.history['loss'], label='loss')
    ax.set_ylim([0, 2])
    ax.set_xlabel('Epoch')
    ax.set_ylabel('loss (cost)')
    ax.legend()
    ax.grid(True)
    plt.show()

plot_loss_tf(his)

4.4 预测

最大的输出是 prediction[2]，表明预测的数字是 ‘2’。如果问题只需要选择一个答案，那就足够了。可以使用 NumPy 的 argmax 来选择它。如果问题需要概率，则需要使用softmax。为了返回一个表示预测目标的整数，您需要找到具有最大概率的索引。可以使用 Numpy 的 argmax 函数实现该功能。

image_of_two = x[1015]
display_digit(image_of_two)

prediction = model.predict(image_of_two.reshape(1,400))  # prediction

print(f" predicting a Two: \n{prediction}")
print(f" Largest Prediction index: {np.argmax(prediction)}")

1/1 [==============================] - 0s 127ms/step
 predicting a Two: 
[[-14.26  11.12  18.87  -0.1  -13.1  -10.73 -13.67  10.45  -3.36 -24.12]]
 Largest Prediction index: 2

prediction_p = tf.nn.softmax(prediction)

print(f" 概率: \n{prediction_p}")
print(f"概率之和: {np.sum(prediction_p):0.3f}")

 概率: 
[[4.08e-15 4.30e-04 9.99e-01 5.76e-09 1.31e-14 1.40e-13 7.40e-15 2.20e-04
  2.22e-10 2.13e-19]]
概率之和: 1.000

yhat = np.argmax(prediction_p)

print(f"np.argmax(prediction_p): {yhat}")

np.argmax(prediction_p): 2

import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
# You do not need to modify anything in this cell

m, n = x.shape

fig, axes = plt.subplots(8,8, figsize=(5,5))
fig.tight_layout(pad=0.13,rect=[0, 0.03, 1, 0.91]) #[left, bottom, right, top]
widgvis(fig)
for i,ax in enumerate(axes.flat):
    # Select random indices
    random_index = np.random.randint(m)

    # Select rows corresponding to the random indices and
    # reshape the image
    X_random_reshaped = x[random_index].reshape((20,20)).T

    # Display the image
    ax.imshow(X_random_reshaped, cmap='gray')

    # Predict using the Neural Network
    prediction = model.predict(x[random_index].reshape(1,400))
    prediction_p = tf.nn.softmax(prediction)
    yhat = np.argmax(prediction_p)

    # Display the label above the image
    ax.set_title(f"{y[random_index,0]},{yhat}",fontsize=10)
    ax.set_axis_off()
fig.suptitle("Label, yhat", fontsize=14)
plt.show()

1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 26ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 32ms/step
1/1 [==============================] - 0s 32ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 25ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 33ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 27ms/step
1/1 [==============================] - 0s 34ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 33ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 37ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 35ms/step
1/1 [==============================] - 0s 34ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 34ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 32ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 37ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 31ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 27ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 32ms/step
1/1 [==============================] - 0s 36ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 29ms/step

让我们来看看一些错误。

注意：增加训练时期的数量可以消除此数据集上的错误。

print( f"{display_errors(model,x,y)} errors out of {len(x)} images")

157/157 [==============================] - 0s 1ms/step
1/1 [==============================] - 0s 29ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 28ms/step
1/1 [==============================] - 0s 39ms/step
1/1 [==============================] - 0s 30ms/step
1/1 [==============================] - 0s 52ms/step
1/1 [==============================] - 0s 27ms/step
61 errors out of 5000 images

文章来源地址https://www.toymoban.com/news/detail-486666.html

到了这里，关于吴恩达471机器学习入门课程2第2周——手写数字识别（0到9）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！