【程序员面试金典】面试题 17.13. 恢复空格

这篇具有很好参考价值的文章主要介绍了【程序员面试金典】面试题 17.13. 恢复空格。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

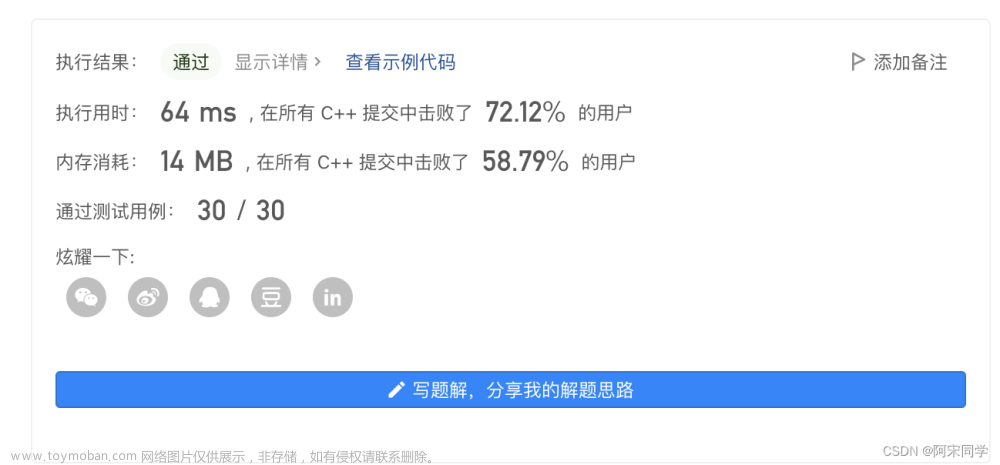
题目描述

描述：哦，不！你不小心把一个长篇文章中的空格、标点都删掉了，并且大写也弄成了小写。像句子"I reset the computer. It still didn’t boot!“已经变成了"iresetthecomputeritstilldidntboot”。在处理标点符号和大小写之前，你得先把它断成词语。当然了，你有一本厚厚的词典dictionary，不过，有些词没在词典里。假设文章用sentence表示，设计一个算法，把文章断开，要求未识别的字符最少，返回未识别的字符数。

注意：本题相对原题稍作改动，只需返回未识别的字符数

示例：

输入：
dictionary = ["looked","just","like","her","brother"]
sentence = "jesslookedjustliketimherbrother"
输出： 7
解释： 断句后为"jess looked just like tim her brother"，共7个未识别字符。

提示：

0 <= len(sentence) <= 1000
dictionary中总字符数不超过 150000。
你可以认为dictionary和sentence中只包含小写字母。

解题思路

思路：最直观的想法是，动态规划+字典树。使用dp[i]表示长度为i的字符串的最少未识别字符，如果下标0_i-1(长度1i)之间未匹配，则dp[i]=dp[i-1]+1，反之如果下标j-1_i-1(长度ji)之间发生匹配，则dp[i]=dp[j-1]+1，其中字典树需要逆序构建喔！

class Trie {
public:
	//下一个字母
    Trie* next[26];
    //该字符是否是该单词的结束位置
    bool isEnd;
    //前缀树类的构造函数
    Trie(){
        isEnd=false;
        memset(next,0,sizeof(next));
    }
    //向字典树中插入单词(可根据需求选择正序或者逆序插入)
    void insert(string s)
    {
        //逆序插入
        Trie* curPos=this;
        for(int i=s.size()-1;i>=0;i--)
        {
            int t=s[i]-'a';
            if(curPos->next[t]==nullptr)
                curPos->next[t]=new Trie();
            curPos=curPos->next[t];
        }
        curPos->isEnd=true;
    }
};
class Solution {
public:
    int respace(vector<string>& dictionary, string sentence) {
        int n=sentence.size();
        int m=dictionary.size();
        //创建字典树对象 使用指针root指向该对象
        Trie* root=new Trie();
        //构建字典树
        for(auto dic:dictionary)
        {
            root->insert(dic);
        }
        //dp[i]表示以长度为i结尾的最少未识别字符
        vector<int> dp(n+1,INT_MAX);
        //长度为0的字符串未识别的为0
        dp[0]=0;
        //i表示第几个字符
        for(int i=1;i<=n;i++)
        {
            dp[i]=dp[i-1]+1;
            Trie* curPos=root;
            //j表示第几个字符
            for(int j=i;j>=1;j--)
            {
                //字符对应的下标
                int t=sentence[j-1]-'a';
                //如果当前字符在字典树中不存在则直接退出
                if(curPos->next[t]==nullptr)
                    break;
                //如果当前字符在字典树中且已经结束则求取最小长度
                else if(curPos->next[t]->isEnd) 
                    dp[i]=min(dp[i],dp[j-1]);
                curPos=curPos->next[t];
            }
        }
        return dp[n];
    }
};

总结：注意字典树的数据结构编写方式！！！root->insert！！！

字典树介绍

实现 Trie (前缀树)

前缀树是一种树形数据结构，用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用情景，例如自动补完和拼写检查。

请你实现 Trie 类：

Trie() 初始化前缀树对象。
void insert(String word) 向前缀树中插入字符串 word 。
boolean search(String word) 如果字符串 word 在前缀树中，返回 true（即，在检索之前已经插入）；否则，返回 false 。
boolean startsWith(String prefix) 如果之前已经插入的字符串 word 的前缀之一为 prefix ，返回 true ；否则，返回 false 。

示例：

输入
["Trie", "insert", "search", "search", "startsWith", "insert", "search"]
[[], ["apple"], ["apple"], ["app"], ["app"], ["app"], ["app"]]
输出
[null, null, true, false, true, null, true]

解释
Trie trie = new Trie();
trie.insert("apple");
trie.search("apple");   // 返回 True
trie.search("app");     // 返回 False
trie.startsWith("app"); // 返回 True
trie.insert("app");
trie.search("app");     // 返回 True

提示：

1 <= word.length, prefix.length <= 2000
word 和 prefix 仅由小写英文字母组成
insert、search 和 startsWith 调用次数总计不超过 3 * 104 次

思路：最直观的想法是，字典树。字典树，一次建树，多次查询。

class Trie {
private:
    bool isEnd; //标记是否为单词结尾
    Trie* next[26]; //标记下一个节点可能是什么 分别是a,b,c,d...
public:
    Trie() {
        isEnd=false;
        memset(next,0,sizeof(next));
    }
    void insert(string word) {
        //首先指向当前这棵树
        Trie* node=this;
        //遍历单词
        for(char c:word)
        {
            //如果对应为空则新建
            if(node->next[c-'a']==NULL)
                node->next[c-'a']=new Trie();
            //然后将节点指向当前(为下一次准备)
            node=node->next[c-'a'];
        }
        //置单词结束标志
        node->isEnd=true;
    }
    bool search(string word) {
        //首先指向当前这棵树
        Trie* node=this;
        for(char c:word)
        {
            node=node->next[c-'a'];
            if(node==NULL)
                return false;
        }
        return node->isEnd;
    }
    bool startsWith(string prefix) {
        //首先指向当前这棵树
        Trie* node=this;
        for(char c:prefix)
        {
            node=node->next[c-'a'];
            if(node==NULL)
                return false;
        }
        return true;
    }
};

总结：字典树一般用于单词查找和前缀匹配。文章来源地址https://www.toymoban.com/news/detail-500508.html

到了这里，关于【程序员面试金典】面试题 17.13. 恢复空格的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！