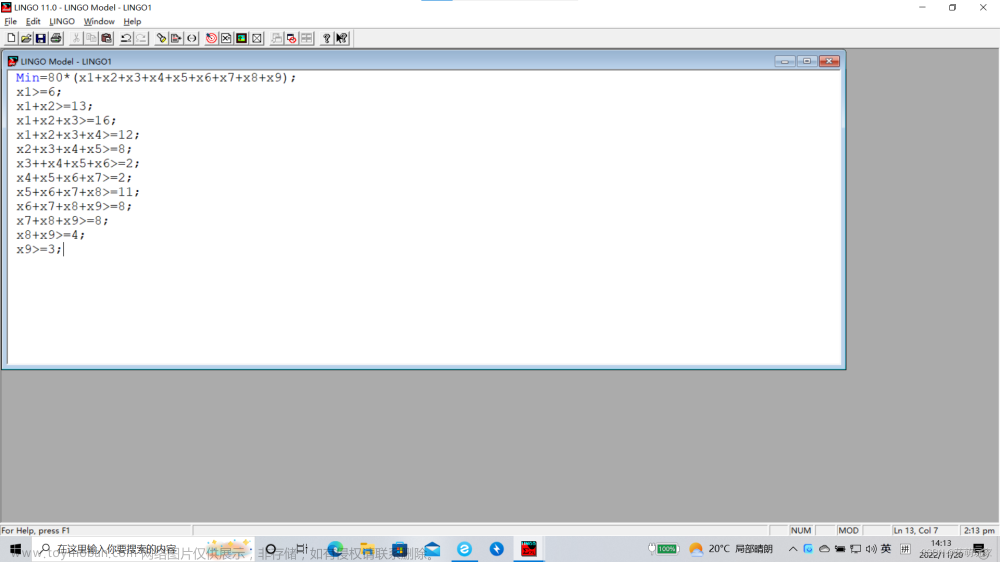
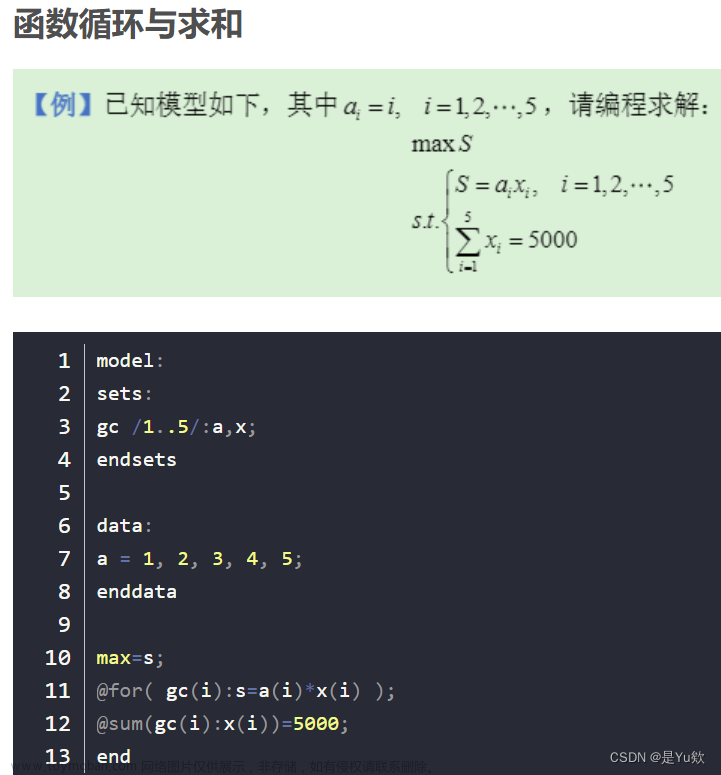
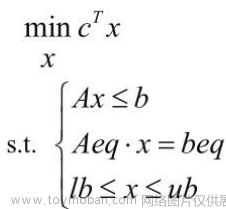lingo软件求解线性规划举例-Toy模板网

这篇具有很好参考价值的文章主要介绍了lingo软件求解线性规划举例。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

lingo软件求解线性规划举例,数学建模案例,算法,数学建模

方法一（直接解）

代码

min=4*x11+12*x12+4*x13+11*x14
    +2*x21+10*x22+3*x23+9*x24
      +8*x31+5*x32+11*x33+6*x34;
x11+x12+x13+x14=16;
x21+x22+x23+x24=10;
x31+x32+x33+x34=22;
x11+x21+x31=8;
x12+x22+x32=14;
x13+x23+x33=12;
x14+x24+x34=14;

结果

  Global optimal solution found.
  Objective value:                              244.0000
  Infeasibilities:                              0.000000
  Total solver iterations:                             7


                       Variable           Value        Reduced Cost
                            X11        0.000000            0.000000
                            X12        0.000000            2.000000
                            X13        12.00000            0.000000
                            X14        4.000000            0.000000
                            X21        8.000000            0.000000
                            X22        0.000000            2.000000
                            X23        0.000000            1.000000
                            X24        2.000000            0.000000
                            X31        0.000000            9.000000
                            X32        14.00000            0.000000
                            X33        0.000000            12.00000
                            X34        8.000000            0.000000

                            Row    Slack or Surplus      Dual Price
                              1        244.0000           -1.000000
                              2        0.000000           -4.000000
                              3        0.000000           -2.000000
                              4        0.000000            1.000000
                              5        0.000000            0.000000
                              6        0.000000           -6.000000
                              7        0.000000            0.000000
                              8        0.000000           -7.000000

缺点，数据多时不好找

方法二（化简）

当变量有成千上万个时，而关心的非零解只是极少数，在当前窗口读解很麻烦。下面是读取非零解的窗口操作步骤：

（1）缩小当前解的窗口（不是关闭！）；

（2）把鼠标点进模型所在窗口；

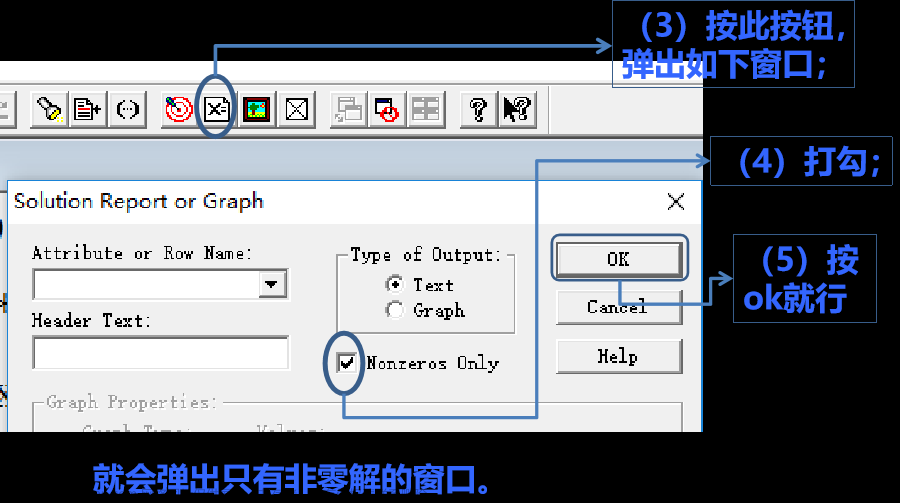lingo软件求解线性规划举例,数学建模案例,算法,数学建模文章来源地址https://www.toymoban.com/news/detail-536777.html

结果

  Global optimal solution found.
  Objective value:                              244.0000
  Infeasibilities:                              0.000000
  Total solver iterations:                             7


                       Variable           Value        Reduced Cost
                            X13        12.00000            0.000000
                            X14        4.000000            0.000000
                            X21        8.000000            0.000000
                            X24        2.000000            0.000000
                            X32        14.00000            0.000000
                            X34        8.000000            0.000000

                            Row    Slack or Surplus      Dual Price
                              2        0.000000           -4.000000
                              3        0.000000           -2.000000
                              4        0.000000            1.000000
                              5        0.000000            0.000000
                              6        0.000000           -6.000000
                              7        0.000000            0.000000
                              8        0.000000           -7.000000

到了这里，关于lingo软件求解线性规划举例的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！