定义
图通常以一个二元组 G=<V, E>表示,V表示节点集,E表示边集。节点集中元素的个数,称为图的阶。
若图G中的每条边都是没有方向的,称为无向图;每条边是由两个节点组成的无序对,例如节点V1和节点V2之间的边,记为

若图G中的每条边都是有方向的,称为有向图;有向边也称为弧,每条弧是有两个节点组成的有序对,例如节点V1和节点V2之间的弧,记为<V1, V2>
定理
握手定理:所有节点的度数之和等于边数的两倍。
存储
邻接表是图的一种链式存储结构,包括两部分:节点和邻接点。
邻接点结构
struct LinkNode {
int nodeIndex; // 节点下标
// int weight; // 路径上有不同权重,可以使用
LinkNode *next; // 下一个邻接点
};
节点
struct Node {
char ch; // 节点名称,假定为单字符
LinkNode *first; // 第一个邻接点
}
节点数组
Node nodes[26]; // 26个字符
示例:
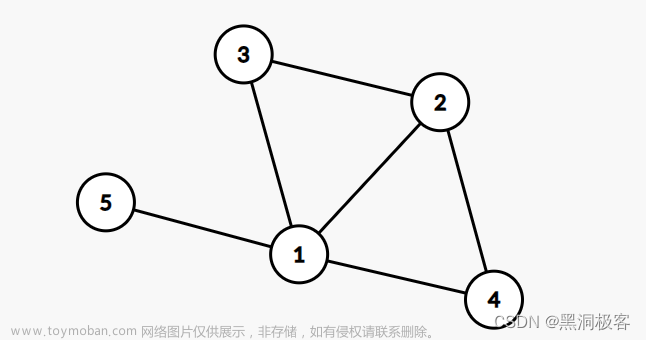
有如下图: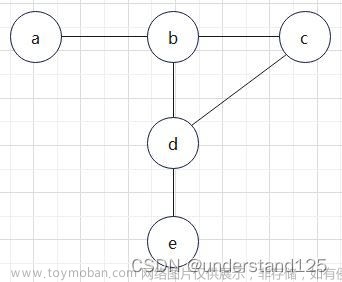
邻接表结构: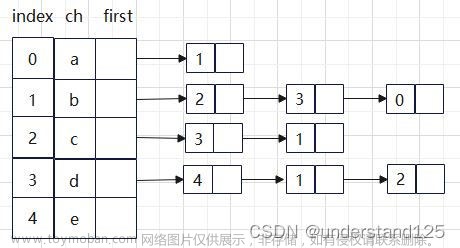
图的搜索
广度优先搜索
广度优先搜索(Breadth First Search, BFS),又称为宽度优先搜索。即从某个节点(源点)出发,优先访问该节点的所有未被访问的邻接点,再依次从这些被访问的点出发,一层一层的访问,直到访问节点均已访问。如存储的示例图,访问顺序如下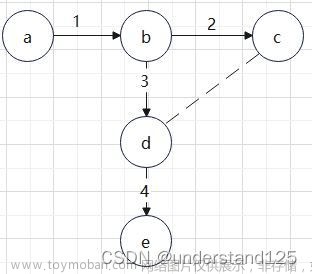
深度优先搜索
深度优先搜索(Depth First Search, DFS)。即优先沿着一条路径搜索,直到当前节点无未被访问的邻接点,则退回到上一个节点,继续访问其未被访问的邻接点,直到所有点均已访问。如存储的示例图,访问顺序如下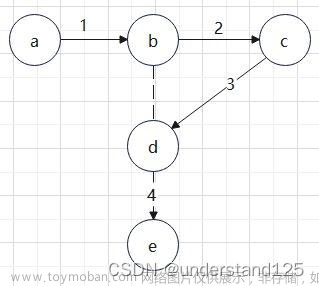 文章来源:https://www.toymoban.com/news/detail-601936.html
文章来源:https://www.toymoban.com/news/detail-601936.html
图的连通性
- 无向图的连通分量
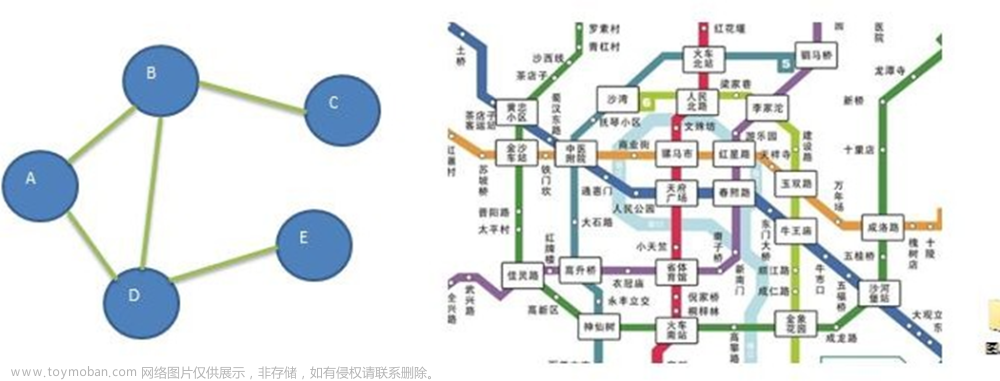
在无向图中,如果从节点Vi到节点Vj有路径,则称节点Vi和节点Vj是连通的。如果途中任意两个节点都是连通的,则称图G为连通图。连通分量,即其子连通图。如下图,为连通图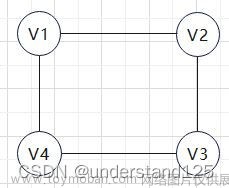
- 有向图的强连通分量
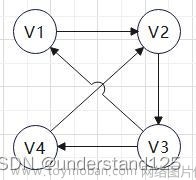
在有向图中,如果图中的任意两个节点从Vi到Vj都有路径,且从Vj到Vi也有路径,则称图G为强连通图。强连通分量,即其子强连通图。如下图,为强连通图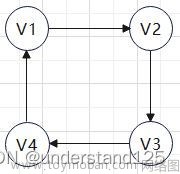
- 桥和割点
如果去掉无向图G中的一条边Ei后,图G分裂为两个不相连的子图,那么Ei为图G的桥,或称割边;如果去掉无向图G中的一个节点Vi,及与Vi关联的所有边后,图G分裂为两个或两个以上不相连的子图,那么Vi称为图G的割点。
如存储的示例图,去掉d到e的边,则原图分裂为两个不连通的子图,因此,d到e的边,为图的桥
如存储的示例图,去掉节点d,及与d相连的边,则原图分裂为两个不连通的子图,因此,节点d为图的割点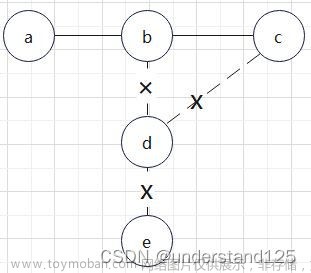
桥与割点的关系:有割点不一定有桥,有乔一定有割点;桥一定是割点依附的边
桥与割点的算法:Tarjan算法 - 无向图的双连通分量(DCC)
如果无向图中不存在桥,则称为边双连通图。图中任意两点之间都存在两条或两条以上的路径,且路径上的边互不重复。极大边双连通图,称为边双连通分量(e-DCC)。
如果无向图中不存在割点,则称为点双连通图。图中,如果节点数大于2,则在任意两点间都存在两条或两条以上路径,且路径上的点互不重复。极大点双连通子图称为点双连通分量(v-DCC)。 - 双连通分量的缩点
把每一个边双连通分量都看作一个点,把桥看作连接连个缩点的无向边,可得到一棵树,这种方法被称为边连通分量缩点。如图,虚线内看作一个节点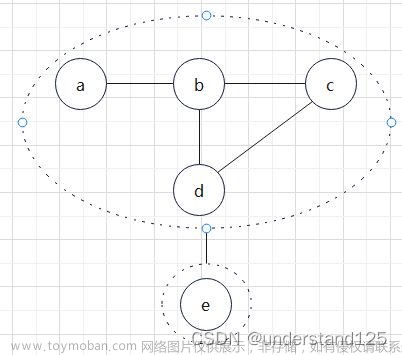
把每一个点双连通分量都看作一个点,把割点看作一个点,每个割点都向包含它的点双连通分量连接一条边,得到一棵树,这种方法称为点双连通分量缩点。如图,虚线内看作一个节点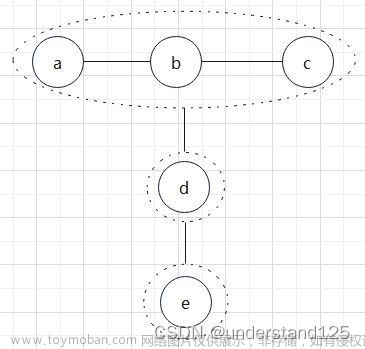
参考《算法训练营》文章来源地址https://www.toymoban.com/news/detail-601936.html
到了这里,关于算法之图论的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!