LeetCode221.Maximal-Square＜最大正方形＞

这篇具有很好参考价值的文章主要介绍了LeetCode221.Maximal-Square＜最大正方形＞。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目：

LeetCode221.Maximal-Square＜最大正方形＞,算法,leetcode,数据结构,c++,动态规划

思路：

这题是动态规划，但是不会写。想着判断dp的 <上，左，左上> 去了。发现只能这样最大只能判断面积为4的正方形因为只会判断另外三个方格。而要想判断更大的正方形那就需要递归操作了。那肯定会超时了。

好吧，只能看答案了。

正方形的面积的长乘宽。在例子中我们可以看到有一个长方形。但是我们只取短的边作为正方形的边。所以dp是取最小值。

LeetCode221.Maximal-Square＜最大正方形＞,算法,leetcode,数据结构,c++,动态规划

代码是：

//code
 
class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty()) {
            return 0;//当vector是空的时候返回0
        }
        int m = matrix.size(), n = matrix[0].size();//m是矩阵的行 n是列
        vector<vector<int>> dp(m, vector<int>(n, 0));//创建m行 n列的二维数组并且值都是0
        int ans = 0;//初始化ans
        for (int i = 0; i < m; i++) {
            for (int j = 0; j < n; j++) {
                if (matrix[i][j] == '1') {//遍历矩阵,当矩阵的值为1时才进行动态规划.
                    if (i == 0 || j == 0) {//当处在边缘时.值只能为1. 
                        dp[i][j] = 1;    //因为取的正方形是以右下角向前面进行相加.
                    } else {
                        dp[i][j] = min({dp[i-1][j], dp[i][j-1], dp[i-1][j-1]}) + 1;//获得边长.
                    }
                    ans = max(ans, dp[i][j]);//获得最大的边长.
                }
            }
        }
        return ans * ans;//返回面积
    }
};

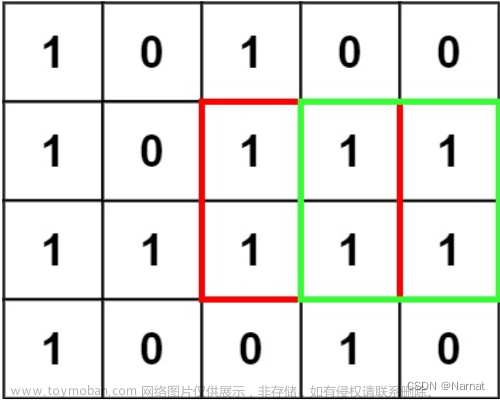
在获得边长这一部中,我们取三个点是左, 上, 左上. 因为原本可能是长方形

LeetCode221.Maximal-Square＜最大正方形＞,算法,leetcode,数据结构,c++,动态规划