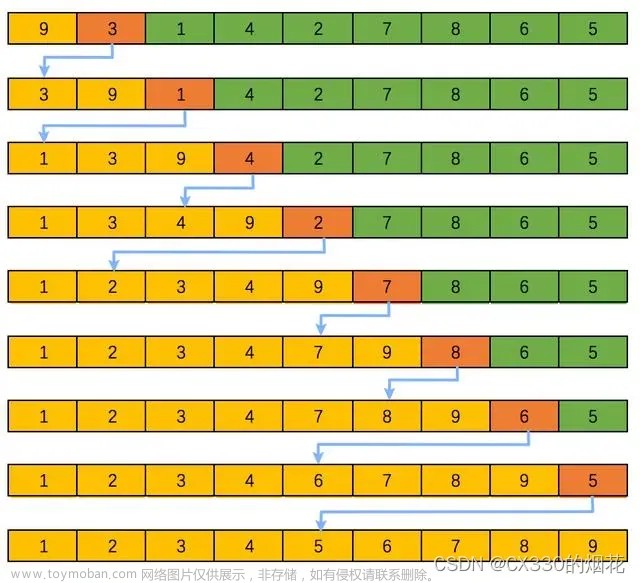
起因:
二郎最近在研究LBL(长基线)定位,大部分论文都提到了文中算法获得的方差接近CRB,所以自己的算法性能较好。于是二郎就想知道克拉美罗界是什么意思,以及能应用的场景。
经过:
1)查文档:
克拉美罗界:为无偏估计量的方差确定一个下界,衡量无偏估计的性能。
无偏估计:估计方法获得结果的平均值和真实值的差为0,这里通俗一点讲是,我用一种方法,获得一个结果,这个结果是在真实结果的附近波动,并且结果的平均误差为0(高斯、0均值扰动)。
方差:统计学的定理,描述了一组数据中单个数据与数据的平均值之间的差异,用于反应数据的波动程度(这里说方差其实有两个对象:1)计算/测量结果:方差可以说明计算/测量是否稳定,在输入存在波动时,输出是否还能稳定;2)数据:这里仅仅表示了数据的波动情况,没有什么实质的含义)
下界:方差的下界一般认为是能达到的最好结果,即,我有一组带有方差的输入,获得输出,那么输出结果的波动程度是不会小于这个下界的,也就是说我结果越接近这个下界,我算法的性能越好。
无偏估计的性能:包括准确性(偏差)和稳定性(方差)
2)存在问题:
查文档后,二郎对CRB有了一个初步了解,这里存在疑惑
①输入数据的方差怎么获得?
②CRB只需要知道我输入数据的方差,就能得到整个定位算法的CRB么?完全不需要管我如何使用的这些数据?以及这些数据和最终结果的关系?
①很多人以及很多方程都会讲,使用方差,但是他们并没有说方差怎么来的
二郎推断,方差可以这么来:实测和理论
实测:一个数据是由一个或多个设备获得的,利用设备测量大量的数据,可以获得设备测量的方差,如果有真实值,还可以判断是否是无偏。实测获得方差后,就可以拿回实验室,去用CRB计算我们的下边界了。
理论:学术上或者工程上,有很多人分享了,不同测量设备获得的数据的方差在哪个范围,在研究中,我们可以直接拿来用,认为数据是存在这样的方差。
②CRB和估计方法无关(也就是我们如何利用数据,计算结果的公式),只是通过已有数据,获得最好的估计结果。
先学习两个名词
似然函数:对于给定的观测数据,似然函数表示在不同参数值的条件下,观测数据的概率密度或概率质量。(也就是说,似然函数就是一个函数,这个函数能反应数据的统计规律。函数使用不同参数,反应的统计规律不同。要想找到最能反应当前一组数据的统计规律的参数,就要用到最大似然估计方法)(高斯分布/正太分布就是似然函数的一种,求里面的参数:均值和方差,就是最大似然估计解决的问题)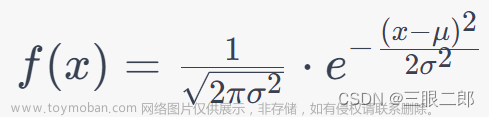
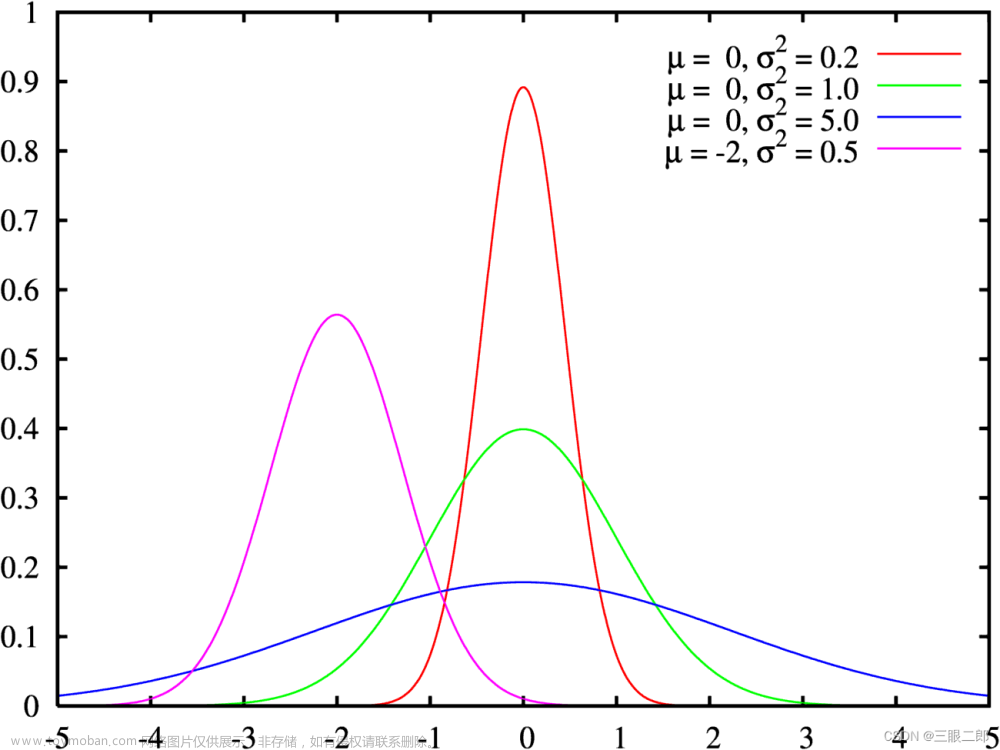
这里为啥要提似然函数?
因为CRB研究的是方差的下界,而似然函数是描述误差分布的函数,方差越小,正太分布(一种常用的似然函数)的峰值越高,表示得到估计结果的精度越高,而这个精度的下边界,就是CRB要求解的问题。
似然函数会涉及到函数之间的相乘,为了方便,把乘法变成加法(这里用的最多的是声学,用了dB,分贝,把所有的乘法都变成了加法,把所有的除法都变成了减法,以至于,很多人说,看不懂)
对数似然函数:求似然函数的对数,也就是加一个lg或者ln,很简单,不用想太复杂,只是一个表现形式的差异性质不变。似然函数取极值的地方,对数似然函数同样是取极值。
函数一阶导:斜率,变化速率。横轴取x时,导数等于0,表示函数在x点取极值。
函数二阶导:曲率,弯曲程度。二阶导为0,表示凹凸发生了变化,表示该点为极值点或者拐点。
对于以x为变量的高斯函数而言,其拐点在x=μ(均值);
对对数似然函数进行求导
发现函数的二阶导是个固定值,只和σ有关,高斯函数的曲率不随x改变而改变。二阶导绝对值越大,证明曲率越大,越陡峭。二阶导值小于0表示函数的曲线向上突,为了能把二阶导越大对应到越陡峭,因此需要负的二阶导数。
这样就可以说,似然函数(高斯函数)的负的二阶导数越大,函数越陡峭,利用符合这样分布的一组数据估计出的结果越准确。
上面是高斯函数对x进行求导,这个很好理解,但是在计算CRB时,求导的变量为平均值μ,其实是和x获得一样的结果
似然函数的负的二阶导的导数,就是RCB
3)多数据组合的CRB:
上面我们也会发现,我们求解CRB只用了一组数据
如果我们估计最终结果,需要多个数据,如果这几个数据独立,那么最终结果是所有方差的累加。
得到一个结果需要多个输入数据
这里有一个误区,这里其实不是简单的数据的方差相加,而是数据的方差乘以对应的系数平方,然后相加
例如,上面是对一个数据的多次测量,取平均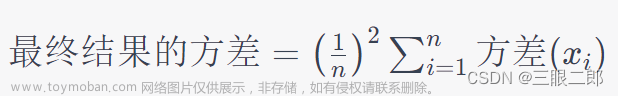
因此最终结果的方差为σ²/n
那么,对应的CRB为σ²/n

上面给出了期望,其实就是组成最终结果的每个变量对应的系数,例如,求平均,每个变量对那个的系数就是1/n
,乘以系数再相加
到这里会存在一个非常大的疑问,Fisher信息中,θ是它的待估计参数,而上面个一直在说对x求导。
费希尔信息(Fisher Information)(有时简称为信息[1])是一种测量可观察随机变量X携带的关于模型X的分布的未知参数θ的信息量的方法。
意思就是说,我有一组测量的数据X,我不知道它们是如何分布的,但是我能通过Fisher信息判断,我从当前这些数据X中,估计其分布(也就是获得似然函数参数)的靠谱程度。这楼里的信息量指,手里拿的这些数据,反应整体数据分布的可靠性(置信概率)。
高斯函数的参数θ有均值μ和方差σ2
这里的费希尔信息是高斯函数对μ求二阶导,结果和对x求二阶导一致,所以上面容易造成误导(高斯函数的均值μ更好确定,而且更多信息包含在该信息上面,因此这里用μ来求整体的信息量)
CRB是Fisher信息的倒数→CRB是Fisher信息的倒数→CRB是Fisher信息的倒数文章来源:https://www.toymoban.com/news/detail-617100.html
小知识:
1)贝叶斯统计:用于处理不确定性和随机性的问题,将主观先验知识(在求一组数据的概率分布时,我们会事先假设它符合哪种分布,对应哪种似然函数,似然函数的参数大概是多少)与数据(观察到的实际数据)相结合,从而得出关于参数的后验概率分布(先验+数据,得到的概率分布,就是后验概率分布)。文章来源地址https://www.toymoban.com/news/detail-617100.html
- 先验概率分布:在收集数据之前,我们通常有一些主观的先验知识或经验,用一个概率分布来描述参数的不确定性。
- 似然函数:通过收集实验或观测数据,我们可以得到似然函数,它描述了在给定参数下观察到数据的可能性。
- 后验概率分布:利用贝叶斯定理,将先验概率分布和似然函数相结合,得出关于参数的后验概率分布。后验概率是在考虑了先验知识和实验数据后,参数值的可能性。
- 贝叶斯估计:从后验概率分布中提取有关参数的信息,例如计算均值、中位数、最大似然估计等,用于参数估计和推断。
到了这里,关于一篇文章搞定克拉美罗界(CRB)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!