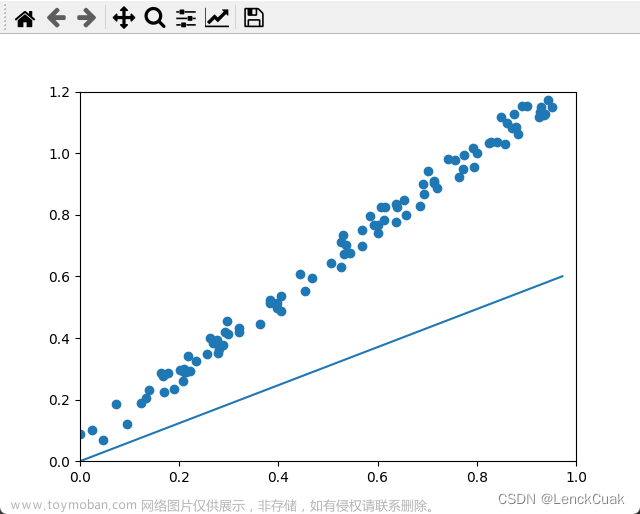
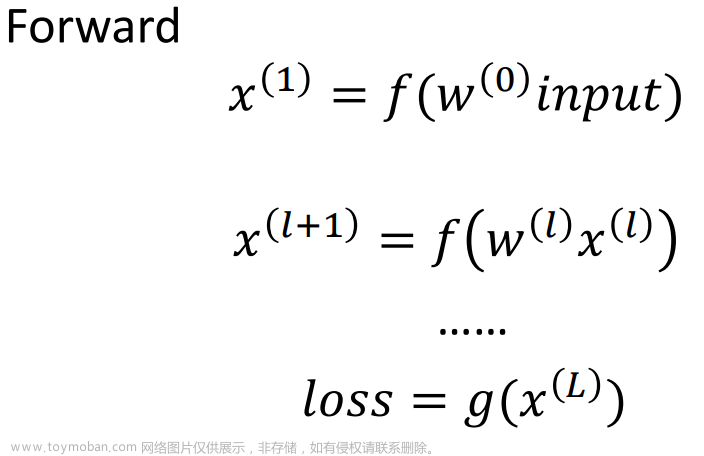pytorch实现梯度下降算法例子

这篇具有很好参考价值的文章主要介绍了pytorch实现梯度下降算法例子。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

如题，利用pytorch，通过代码实现机器学习中的梯度下降算法，求解如下方程：
${f}'(x,y) = x^2 + 20 y^2$
的最小值。

Latex语法参考：https://blog.csdn.net/ViatorSun/article/details/82826664


import numpy as np
import matplotlib.pyplot as plt
import matplotlib as mpl
import math
from mpl_toolkits.mplot3d import Axes3D
import warnings
import decimal


# 原函数
def Z(x,y):
    return x**2 + 20*(y**2)

# x方向上的梯度
def dx(x):
    return 2*x

# y方向上的梯度
def dy(y):
    return 40*y

# 初始值
X = x_0 = np.float64(3000.0)
Y = y_0 = np.float64(300.0)

# 学习率
alpha = 0.01

# 保存梯度下降所经过的点
globalX = [x_0]
globalY = [y_0]
globalZ = [Z(x_0,y_0)]

cnt = 0

# 迭代30次
while True:
    lastZ = Z(X,Y)
    temX = X - alpha * dx(X)
    temY = Y - alpha * dy(Y)
    temZ = Z(temX, temY)
    if(lastZ - temZ <= 0.00001):
        break;
    if(cnt >= 1000000):
        break;
    # X,Y 重新赋值
    X = temX
    Y = temY
    
    # 将新值存储起来
    globalX.append(temX)
    globalY.append(temY)
    globalZ.append(temZ)
    cnt = cnt +1
    
    
    
plt.figure(figsize=(8,3))
plt.subplot(111)

plt.ylabel('Y')
plt.xlabel('X')

plt.plot(globalZ)
plt.show()
# 打印结果
print(u"最终结果为:(x,y,z)=(%.5f, %.5f, %.5f),迭代次数：%d" % (X, Y, Z(X,Y),cnt))
print(u"迭代过程中取值")
num = len(globalX)
for i in range(num):
    print(u"第%d次迭代：%.5f, y%d=%.5f, z%d=%.5f" % (i,globalX[i],i,globalY[i],i,globalZ[i]))

输出结果：

pytorch实现梯度下降算法例子,pytorch,算法,人工智能
最终结果为:(x,y,z)=(397.85867, 0.00000, 158291.51945),迭代次数：100
迭代过程中取值
第0次迭代：3000.00000, y0=300.00000, z0=10800000.00000
第1次迭代：2940.00000, y1=180.00000, z1=9291600.00000
第2次迭代：2881.20000, y2=108.00000, z2=8534593.44000
第3次迭代：2823.57600, y3=64.80000, z3=8056562.22778
第4次迭代：2767.10448, y4=38.88000, z4=7687100.29124
第5次迭代：2711.76239, y5=23.32800, z5=7364539.17367
第6次迭代：2657.52714, y6=13.99680, z6=7066368.72182
第7次迭代：2604.37660, y7=8.39808, z7=6784188.02823
第8次迭代：2552.28907, y8=5.03885, z8=6514687.28512
第9次迭代：2501.24329, y9=3.02331, z9=6256400.78564
第10次迭代：2451.21842, y10=1.81399, z10=6008537.55665
第11次迭代：2402.19405, y11=1.08839, z11=5770559.95657
第12次迭代：2354.15017, y12=0.65303, z12=5542031.55767
第13次迭代：2307.06717, y13=0.39182, z13=5322561.98712
第14次迭代：2260.92582, y14=0.23509, z14=5111786.68892
第15次迭代：2215.70731, y15=0.14106, z15=4909359.27237
第16次迭代：2171.39316, y16=0.08463, z16=4714948.40627
第17次迭代：2127.96530, y17=0.05078, z17=4528236.36337
第18次迭代：2085.40599, y18=0.03047, z18=4348918.17242
第19次迭代：2043.69787, y19=0.01828, z19=4176701.00164
第20次迭代：2002.82392, y20=0.01097, z20=4011303.63796
第21次迭代：1962.76744, y21=0.00658, z21=3852456.01246
第22次迭代：1923.51209, y22=0.00395, z22=3699898.75384
第23次迭代：1885.04185, y23=0.00237, z23=3553382.76300
第24次迭代：1847.34101, y24=0.00142, z24=3412668.80552
第25次迭代：1810.39419, y25=0.00085, z25=3277527.12080
第26次迭代：1774.18631, y26=0.00051, z26=3147737.04681
第27次迭代：1738.70258, y27=0.00031, z27=3023086.65975
第28次迭代：1703.92853, y28=0.00018, z28=2903372.42802
第29次迭代：1669.84996, y29=0.00011, z29=2788398.87987
第30次迭代：1636.45296, y30=0.00007, z30=2677978.28423
第31次迭代：1603.72390, y31=0.00004, z31=2571930.34417
第32次迭代：1571.64942, y32=0.00002, z32=2470081.90254
第33次迭代：1540.21643, y33=0.00001, z33=2372266.65920
第34次迭代：1509.41210, y34=0.00001, z34=2278324.89950
第35次迭代：1479.22386, y35=0.00001, z35=2188103.23348
第36次迭代：1449.63938, y36=0.00000, z36=2101454.34543
第37次迭代：1420.64660, y37=0.00000, z37=2018236.75335
第38次迭代：1392.23366, y38=0.00000, z38=1938314.57792
第39次迭代：1364.38899, y39=0.00000, z39=1861557.32064
第40次迭代：1337.10121, y40=0.00000, z40=1787839.65074
第41次迭代：1310.35919, y41=0.00000, z41=1717041.20057
第42次迭代：1284.15200, y42=0.00000, z42=1649046.36903
第43次迭代：1258.46896, y43=0.00000, z43=1583744.13281
第44次迭代：1233.29958, y44=0.00000, z44=1521027.86515
第45次迭代：1208.63359, y45=0.00000, z45=1460795.16169
第46次迭代：1184.46092, y46=0.00000, z46=1402947.67329
第47次迭代：1160.77170, y47=0.00000, z47=1347390.94543
第48次迭代：1137.55627, y48=0.00000, z48=1294034.26399
第49次迭代：1114.80514, y49=0.00000, z49=1242790.50714
第50次迭代：1092.50904, y50=0.00000, z50=1193576.00305
第51次迭代：1070.65886, y51=0.00000, z51=1146310.39333
第52次迭代：1049.24568, y52=0.00000, z52=1100916.50176
第53次迭代：1028.26077, y53=0.00000, z53=1057320.20829
第54次迭代：1007.69555, y54=0.00000, z54=1015450.32804
第55次迭代：987.54164, y55=0.00000, z55=975238.49505
第56次迭代：967.79081, y56=0.00000, z56=936619.05064
第57次迭代：948.43499, y57=0.00000, z57=899528.93624
第58次迭代：929.46629, y58=0.00000, z58=863907.59036
第59次迭代：910.87697, y59=0.00000, z59=829696.84979
第60次迭代：892.65943, y60=0.00000, z60=796840.85453
第61次迭代：874.80624, y61=0.00000, z61=765285.95669
第62次迭代：857.31011, y62=0.00000, z62=734980.63281
第63次迭代：840.16391, y63=0.00000, z63=705875.39975
第64次迭代：823.36063, y64=0.00000, z64=677922.73392
第65次迭代：806.89342, y65=0.00000, z65=651076.99366
第66次迭代：790.75555, y66=0.00000, z66=625294.34471
第67次迭代：774.94044, y67=0.00000, z67=600532.68866
第68次迭代：759.44163, y68=0.00000, z68=576751.59419
第69次迭代：744.25280, y69=0.00000, z69=553912.23106
第70次迭代：729.36774, y70=0.00000, z70=531977.30671
第71次迭代：714.78039, y71=0.00000, z71=510911.00536
第72次迭代：700.48478, y72=0.00000, z72=490678.92955
第73次迭代：686.47509, y73=0.00000, z73=471248.04394
第74次迭代：672.74558, y74=0.00000, z74=452586.62140
第75次迭代：659.29067, y75=0.00000, z75=434664.19119
第76次迭代：646.10486, y76=0.00000, z76=417451.48922
第77次迭代：633.18276, y77=0.00000, z77=400920.41025
第78次迭代：620.51911, y78=0.00000, z78=385043.96200
第79次迭代：608.10872, y79=0.00000, z79=369796.22111
第80次迭代：595.94655, y80=0.00000, z80=355152.29075
第81次迭代：584.02762, y81=0.00000, z81=341088.26004
第82次迭代：572.34707, y82=0.00000, z82=327581.16494
第83次迭代：560.90013, y83=0.00000, z83=314608.95081
第84次迭代：549.68212, y84=0.00000, z84=302150.43636
第85次迭代：538.68848, y85=0.00000, z85=290185.27908
第86次迭代：527.91471, y86=0.00000, z86=278693.94202
第87次迭代：517.35642, y87=0.00000, z87=267657.66192
第88次迭代：507.00929, y88=0.00000, z88=257058.41851
第89次迭代：496.86910, y89=0.00000, z89=246878.90514
第90次迭代：486.93172, y90=0.00000, z90=237102.50049
第91次迭代：477.19309, y91=0.00000, z91=227713.24147
第92次迭代：467.64922, y92=0.00000, z92=218695.79711
第93次迭代：458.29624, y93=0.00000, z93=210035.44354
第94次迭代：449.13032, y94=0.00000, z94=201718.03998
第95次迭代：440.14771, y95=0.00000, z95=193730.00560
第96次迭代：431.34475, y96=0.00000, z96=186058.29738
第97次迭代：422.71786, y97=0.00000, z97=178690.38880
第98次迭代：414.26350, y98=0.00000, z98=171614.24940
第99次迭代：405.97823, y99=0.00000, z99=164818.32513
第100次迭代：397.85867, y100=0.00000, z100=158291.51945文章来源地址https://www.toymoban.com/news/detail-618121.html