前言
本文主要分析Apollo代码中函数
bool Box::HasOverlap(const Box2d &box) const {}的数学原理。
在阅读此部分代码时,第一遍没看懂return的一堆什么意思,百度之后说是采用OBB原理,所以就去了解下OBB原理,回来看还是没太明白,直到看到了博客[1],通过博主的图解才有了进一步的了解,但对照代码还是没能完全理解,后来结合向量的相关知识,才算彻底明白了HasOverlap()实现的具体数学原理。
下面,作者仅对代码进行数学解读。
代码
直接上代码,代码路径/self_driving/Optimization/Apollo-DL-IAPS/util/box2d.cc,作者在这里将代码划分为几个部分分别解读。Apollo对Box2d的碰撞检测分为两步进行,第一步使用AABB进行粗检测(f1部分)快速剔除非碰撞的box,第二部分使用OBB进行细检测(f2~f6部分),对f1检测到有碰撞的box进一步进行检测。
bool Box2d::HasOverlap(const Box2d &box) const {
// f1
if (box.max_x() < min_x() || box.min_x() > max_x() || box.max_y() < min_y() ||
box.min_y() > max_y()) {
return false;
}
//f2
const double shift_x = box.center_x() - center_.x();
const double shift_y = box.center_y() - center_.y();
const double dx1 = cos_heading_ * half_length_;
const double dy1 = sin_heading_ * half_length_;
const double dx2 = sin_heading_ * half_width_;
const double dy2 = -cos_heading_ * half_width_;
const double dx3 = box.cos_heading() * box.half_length();
const double dy3 = box.sin_heading() * box.half_length();
const double dx4 = box.sin_heading() * box.half_width();
const double dy4 = -box.cos_heading() * box.half_width();
//f3
return std::abs(shift_x * cos_heading_ + shift_y * sin_heading_) <=
std::abs(dx3 * cos_heading_ + dy3 * sin_heading_) +
std::abs(dx4 * cos_heading_ + dy4 * sin_heading_) +
half_length_ &&
//f4
std::abs(shift_x * sin_heading_ - shift_y * cos_heading_) <=
std::abs(dx3 * sin_heading_ - dy3 * cos_heading_) +
std::abs(dx4 * sin_heading_ - dy4 * cos_heading_) +
half_width_ &&
//f5
std::abs(shift_x * box.cos_heading() + shift_y * box.sin_heading()) <=
std::abs(dx1 * box.cos_heading() + dy1 * box.sin_heading()) +
std::abs(dx2 * box.cos_heading() + dy2 * box.sin_heading()) +
box.half_length() &&
//f6
std::abs(shift_x * box.sin_heading() - shift_y * box.cos_heading()) <=
std::abs(dx1 * box.sin_heading() - dy1 * box.cos_heading()) +
std::abs(dx2 * box.sin_heading() - dy2 * box.cos_heading()) +
box.half_width();
}
代码分析
f1
AABB检测用于粗检测,根据自车和障碍物的box角点构建两个长宽分别平行于坐标轴的box,查看这两个box(两个虚线box表示)是否有交集,可以直接根据新构建的box的角点的坐标值来判断。如下图所示,通过这种方式可以粗略检测到A、B有碰撞,但是是否真的有碰撞还需要通过OBB进一步检测。
f2
根据OBB检测原理,构建向量如下图所示:
假设有两个Box类型的对象A和B,计算A.HasOverlap(B)的结果。
以下两行代码计算的时A的中心到B的中心的向量
const double shift_x = box.center_x() - center_.x();
const double shift_y = box.center_y() - center_.y();
转换为数学计算为:
a
b
⃗
=
(
x
s
h
i
f
t
,
y
s
h
i
f
t
)
=
(
B
.
x
c
e
n
t
e
r
−
A
.
x
c
e
n
t
e
r
,
B
.
y
c
e
n
t
e
r
−
A
.
y
c
e
n
t
e
r
)
(1)
\vec{ab}=(x_{shift},y_{shift})=(B.x_{center}-A.x_{center},B.y_{center}-A.y_{center})\tag{1}
ab=(xshift,yshift)=(B.xcenter−A.xcenter,B.ycenter−A.ycenter)(1)
以下四行代码是分别计算A的纵向方向(指box的朝向)和横向方向的两个向量,其中纵向方向的向量模为
l
e
n
g
t
h
h
a
l
f
length_{half}
lengthhalf,横向方向的向量模为
w
i
d
t
h
h
a
l
f
width_{half}
widthhalf。
const double dx1 = cos_heading_ * half_length_;
const double dy1 = sin_heading_ * half_length_;
const double dx2 = sin_heading_ * half_width_;
const double dy2 = -cos_heading_ * half_width_;
纵向向量:
v
1
⃗
=
(
d
x
1
,
d
y
1
)
=
A
.
l
e
n
g
t
h
h
a
l
f
⋅
(
cos
(
h
e
a
d
i
n
g
A
)
,
sin
(
h
e
a
d
i
n
g
A
)
)
(2)
\vec{v_1}=(dx1,dy1)=A.length_{half}\cdot(\cos(heading_A),\sin(heading_A))\tag{2}
v1=(dx1,dy1)=A.lengthhalf⋅(cos(headingA),sin(headingA))(2)
横向向量:
v
2
⃗
=
(
d
x
2
,
d
y
2
)
=
A
.
w
i
d
t
h
h
a
l
f
⋅
(
sin
(
h
e
a
d
i
n
g
A
)
,
−
cos
(
h
e
a
d
i
n
g
A
)
)
(3)
\vec{v_2}=(dx2,dy2)=A.width_{half}\cdot(\sin(heading_A),-\cos(heading_A))\tag{3}
v2=(dx2,dy2)=A.widthhalf⋅(sin(headingA),−cos(headingA))(3)
其中,
h
e
a
d
i
n
g
A
heading_A
headingA为A的方向角,则
(
cos
(
h
e
a
d
i
n
g
A
)
,
s
i
n
(
h
e
a
d
i
n
g
A
)
)
(\cos(heading_A),\ sin(heading_A))
(cos(headingA), sin(headingA))为A的单位方向向量,
(
sin
(
h
e
a
d
i
n
g
A
)
,
−
cos
(
h
e
a
d
i
n
g
A
)
(\sin(heading_A),-\cos(heading_A)
(sin(headingA),−cos(headingA)为A的单位法向量(为啥单位法向量这样表示?可参考线性代数相关知识)。
同理,以下四行代码分别计算的是B的纵向方向和横向方向的两个向量,纵向方向向量和横向方向向量的模分别是B的半长 l e n g t h h a l f length_{half} lengthhalf,半宽 w i d t h h a l f width_{half} widthhalf。
const double dx3 = box.cos_heading() * box.half_length();
const double dy3 = box.sin_heading() * box.half_length();
const double dx4 = box.sin_heading() * box.half_width();
const double dy4 = -box.cos_heading() * box.half_width();
纵向向量:
v
3
⃗
=
(
d
x
3
,
d
y
3
)
=
B
.
l
e
n
g
t
h
h
a
l
f
⋅
(
cos
(
h
e
a
d
i
n
g
B
)
,
sin
(
h
e
a
d
i
n
g
B
)
)
(4)
\vec{v_3}=(dx3,dy3)=B.length_{half}\cdot(\cos(heading_B),\sin(heading_B))\tag{4}
v3=(dx3,dy3)=B.lengthhalf⋅(cos(headingB),sin(headingB))(4)
横向向量:
v
4
⃗
=
(
d
x
4
,
d
y
4
)
=
B
.
w
i
d
t
h
h
a
l
f
⋅
(
sin
(
h
e
a
d
i
n
g
B
)
,
−
cos
(
h
e
a
d
i
n
g
B
)
)
(5)
\vec{v_4}=(dx4,dy4)=B.width_{half}\cdot(\sin(heading_B),-\cos(heading_B))\tag{5}
v4=(dx4,dy4)=B.widthhalf⋅(sin(headingB),−cos(headingB))(5)
其中,
h
e
a
d
i
n
g
B
heading_B
headingB为B的方向角,则
(
cos
(
h
e
a
d
i
n
g
B
)
,
s
i
n
(
h
e
a
d
i
n
g
B
)
)
(\cos(heading_B),\ sin(heading_B))
(cos(headingB), sin(headingB))为B的单位方向向量,
(
sin
(
h
e
a
d
i
n
g
B
)
,
−
cos
(
h
e
a
d
i
n
g
B
)
(\sin(heading_B),-\cos(heading_B)
(sin(headingB),−cos(headingB)为A的单位法向量。
f3
f 3 f3 f3表示的是计算往A纵轴上的投影
std::abs(shift_x * cos_heading_ + shift_y * sin_heading_) <=
std::abs(dx3 * cos_heading_ + dy3 * sin_heading_) +
std::abs(dx4 * cos_heading_ + dy4 * sin_heading_) +
half_length_
如下图所示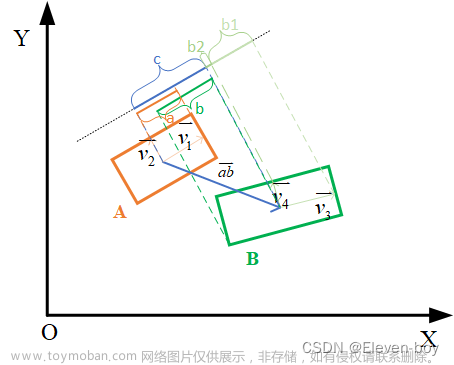
结合代码和图片一块分析:
(1)代码中std::abs(shift_x * cos_heading_ + shift_y * sin_heading_)所表示的是向量
a
b
⃗
\vec{ab}
ab在A的纵轴上投影的模c,结合公式(1)可知:
c
=
∣
a
b
⃗
⋅
(
cos
(
h
e
a
d
i
n
g
A
)
,
sin
(
h
e
a
d
i
n
g
A
)
)
∣
=
∣
x
s
h
i
f
t
⋅
cos
(
h
e
a
d
i
n
g
A
)
+
y
s
h
i
f
t
⋅
sin
(
h
e
a
d
i
n
g
A
)
∣
c=|\vec{ab}\cdot(\cos(heading_A),\sin(heading_A))|=|x_{shift}\cdot\cos(heading_A)+y_{shift}\cdot\sin(heading_A)|
c=∣ab⋅(cos(headingA),sin(headingA))∣=∣xshift⋅cos(headingA)+yshift⋅sin(headingA)∣
(2)代码中std::abs(dx3 * cos_heading_ + dy3 * sin_heading_)所表示的是向量
v
3
⃗
\vec{v_3}
v3在A的纵轴上投影的模
b
1
b1
b1,结合公式(4)可知:
b
1
=
∣
v
3
⃗
⋅
(
cos
(
h
e
a
d
i
n
g
A
)
,
sin
(
h
e
a
d
i
n
g
A
)
)
∣
=
∣
d
x
3
⋅
cos
(
h
e
a
d
i
n
g
A
)
+
d
y
3
⋅
sin
(
h
e
a
d
i
n
g
A
)
∣
b1=|\vec{v_3}\cdot(\cos(heading_A),\sin(heading_A))|=|dx3\cdot\cos(heading_A)+dy3\cdot\sin(heading_A)|
b1=∣v3⋅(cos(headingA),sin(headingA))∣=∣dx3⋅cos(headingA)+dy3⋅sin(headingA)∣
代码中std::abs(dx4 * cos_heading_ + dy4 * sin_heading_)所表示的是向量
v
4
⃗
\vec{v_4}
v4在A的纵轴上投影的模
b
2
b2
b2,结合公式(5)可知:
b
2
=
∣
v
4
⃗
⋅
(
cos
(
h
e
a
d
i
n
g
A
)
,
sin
(
h
e
a
d
i
n
g
A
)
)
∣
=
∣
d
x
4
⋅
cos
(
h
e
a
d
i
n
g
A
)
+
d
y
4
⋅
sin
(
h
e
a
d
i
n
g
A
)
∣
b2=|\vec{v_4}\cdot(\cos(heading_A),\sin(heading_A))|=|dx4\cdot\cos(heading_A)+dy4\cdot\sin(heading_A)|
b2=∣v4⋅(cos(headingA),sin(headingA))∣=∣dx4⋅cos(headingA)+dy4⋅sin(headingA)∣
由上图可知:
b
=
b
1
+
b
2
b=b1+b2
b=b1+b2
(3)代码中half_length_是向量
v
1
⃗
\vec{v_1}
v1在其纵轴上的投影的模,另外,向量
v
2
⃗
\vec{v_2}
v2此时在其纵轴上投影的模为0。
c
1
=
b
+
l
e
n
g
t
h
h
a
l
f
c1=b+length_{half}
c1=b+lengthhalf
f4
f 4 f4 f4表示的是计算往A横轴上的投影
std::abs(shift_x * sin_heading_ - shift_y * cos_heading_) <=
std::abs(dx3 * sin_heading_ - dy3 * cos_heading_) +
std::abs(dx4 * sin_heading_ - dy4 * cos_heading_) +
half_width_
如下图所示
结合代码和图片一块分析:
(1)代码中std::abs(shift_x * sin_heading_ - shift_y * cos_heading_)所表示的是向量
a
b
⃗
\vec{ab}
ab在A的横轴上投影的模c,结合公式(1)可知:
c
=
∣
a
b
⃗
⋅
(
sin
(
h
e
a
d
i
n
g
A
)
,
−
cos
(
h
e
a
d
i
n
g
A
)
)
∣
=
∣
x
s
h
i
f
t
⋅
sin
(
h
e
a
d
i
n
g
A
)
−
y
s
h
i
f
t
⋅
cos
(
h
e
a
d
i
n
g
A
)
∣
c=|\vec{ab}\cdot(\sin(heading_A),-\cos(heading_A))|=|x_{shift}\cdot\sin(heading_A)-y_{shift}\cdot\cos(heading_A)|
c=∣ab⋅(sin(headingA),−cos(headingA))∣=∣xshift⋅sin(headingA)−yshift⋅cos(headingA)∣
(2)代码中std::abs(dx3 * sin_heading_ - dy3 * cos_heading_)所表示的是向量
v
3
⃗
\vec{v_3}
v3在A的横轴上投影的模
b
1
b1
b1,结合公式(4)可知:
b
1
=
∣
v
3
⃗
⋅
(
sin
(
h
e
a
d
i
n
g
A
)
,
−
cos
(
h
e
a
d
i
n
g
A
)
)
∣
=
∣
d
x
3
⋅
sin
(
h
e
a
d
i
n
g
A
)
−
d
y
3
⋅
cos
(
h
e
a
d
i
n
g
A
)
∣
b1=|\vec{v_3}\cdot(\sin(heading_A),-\cos(heading_A))|=|dx3\cdot\sin(heading_A)-dy3\cdot\cos(heading_A)|
b1=∣v3⋅(sin(headingA),−cos(headingA))∣=∣dx3⋅sin(headingA)−dy3⋅cos(headingA)∣
代码中std::abs(dx4 * sin_heading_ - dy4 * cos_heading_)所表示的是向量
v
4
⃗
\vec{v_4}
v4在A的横轴上投影的模
b
2
b2
b2,结合公式(5)可知:
b
2
=
∣
v
4
⃗
⋅
(
sin
(
h
e
a
d
i
n
g
A
)
,
−
cos
(
h
e
a
d
i
n
g
A
)
)
∣
=
∣
d
x
4
⋅
sin
(
h
e
a
d
i
n
g
A
)
−
d
y
4
⋅
cos
(
h
e
a
d
i
n
g
A
)
∣
b2=|\vec{v_4}\cdot(\sin(heading_A),-\cos(heading_A))|=|dx4\cdot\sin(heading_A)-dy4\cdot\cos(heading_A)|
b2=∣v4⋅(sin(headingA),−cos(headingA))∣=∣dx4⋅sin(headingA)−dy4⋅cos(headingA)∣
由上图可知:
b
=
b
1
+
b
2
b=b1+b2
b=b1+b2
(3)代码中half_width_是向量
v
2
⃗
\vec{v_2}
v2在其横轴上的投影的模,另外,向量
v
1
⃗
\vec{v_1}
v1此时在其横轴上投影的模为0。
c
1
=
b
+
w
i
d
t
h
h
a
l
f
c1=b+width_{half}
c1=b+widthhalf
f5
f 5 f5 f5表示的是计算往B纵轴上的投影
std::abs(shift_x * box.cos_heading() + shift_y * box.sin_heading()) <=
std::abs(dx1 * box.cos_heading() + dy1 * box.sin_heading()) +
std::abs(dx2 * box.cos_heading() + dy2 * box.sin_heading()) +
box.half_length()
如下图所示:
结合代码和图片一块分析:
(1)代码中std::abs(shift_x * box.cos_heading() + shift_y * box.sin_heading())所表示的是向量
a
b
⃗
\vec{ab}
ab在B的纵轴上投影的模c,结合公式(1)可知:
c
=
∣
a
b
⃗
⋅
(
cos
(
h
e
a
d
i
n
g
B
)
,
sin
(
h
e
a
d
i
n
g
B
)
)
∣
=
∣
x
s
h
i
f
t
⋅
cos
(
h
e
a
d
i
n
g
B
)
+
y
s
h
i
f
t
⋅
sin
(
h
e
a
d
i
n
g
B
)
∣
c=|\vec{ab}\cdot(\cos(heading_B),\sin(heading_B))|=|x_{shift}\cdot\cos(heading_B)+y_{shift}\cdot\sin(heading_B)|
c=∣ab⋅(cos(headingB),sin(headingB))∣=∣xshift⋅cos(headingB)+yshift⋅sin(headingB)∣
(2)代码中std::abs(dx1 * box.cos_heading() + dy1 * box.sin_heading())所表示的是向量
v
1
⃗
\vec{v_1}
v1在B的纵轴上投影的模
a
1
a1
a1,结合公式(2)可知:
a
1
=
∣
v
1
⃗
⋅
(
cos
(
h
e
a
d
i
n
g
B
)
,
sin
(
h
e
a
d
i
n
g
B
)
)
∣
=
∣
d
x
1
⋅
cos
(
h
e
a
d
i
n
g
B
)
+
d
y
1
⋅
sin
(
h
e
a
d
i
n
g
B
)
∣
a1=|\vec{v_1}\cdot(\cos(heading_B),\sin(heading_B))|=|dx1\cdot\cos(heading_B)+dy1\cdot\sin(heading_B)|
a1=∣v1⋅(cos(headingB),sin(headingB))∣=∣dx1⋅cos(headingB)+dy1⋅sin(headingB)∣
代码中std::abs(dx2 * box.cos_heading() + dy2 * box.sin_heading())所表示的是向量
v
2
⃗
\vec{v_2}
v2在B的纵轴上投影的模
a
2
a2
a2,结合公式(3)可知:
a
2
=
∣
v
2
⃗
⋅
(
cos
(
h
e
a
d
i
n
g
B
)
,
sin
(
h
e
a
d
i
n
g
B
)
)
∣
=
∣
d
x
2
⋅
cos
(
h
e
a
d
i
n
g
B
)
+
d
y
2
⋅
sin
(
h
e
a
d
i
n
g
B
)
∣
a2=|\vec{v_2}\cdot(\cos(heading_B),\sin(heading_B))|=|dx2\cdot\cos(heading_B)+dy2\cdot\sin(heading_B)|
a2=∣v2⋅(cos(headingB),sin(headingB))∣=∣dx2⋅cos(headingB)+dy2⋅sin(headingB)∣
由上图可知:
a
=
a
1
+
a
2
a=a1+a2
a=a1+a2
(3)代码中half_length是向量
v
3
⃗
\vec{v_3}
v3在其纵轴上的投影的模,另外,向量
v
4
⃗
\vec{v_4}
v4此时在其纵轴上投影的模为0。
c
1
=
a
+
l
e
n
g
t
h
h
a
l
f
c1=a+length_{half}
c1=a+lengthhalf
f6
f 6 f6 f6表示的是计算往B横轴上的投影
std::abs(shift_x * box.sin_heading() - shift_y * box.cos_heading()) <=
std::abs(dx1 * box.sin_heading() - dy1 * box.cos_heading()) +
std::abs(dx2 * box.sin_heading() - dy2 * box.cos_heading()) +
box.half_width()
如下图所示:
结合代码和图片一块分析:
(1)代码中std::abs(shift_x * box.sin_heading() - shift_y * box.cos_heading())所表示的是向量
a
b
⃗
\vec{ab}
ab在B的横轴上投影的模c,结合公式(1)可知:
c
=
∣
a
b
⃗
⋅
(
sin
(
h
e
a
d
i
n
g
B
)
,
−
cos
(
h
e
a
d
i
n
g
B
)
)
∣
=
∣
x
s
h
i
f
t
⋅
sin
(
h
e
a
d
i
n
g
B
)
−
y
s
h
i
f
t
⋅
cos
(
h
e
a
d
i
n
g
B
)
∣
c=|\vec{ab}\cdot(\sin(heading_B),-\cos(heading_B))|=|x_{shift}\cdot\sin(heading_B)-y_{shift}\cdot\cos(heading_B)|
c=∣ab⋅(sin(headingB),−cos(headingB))∣=∣xshift⋅sin(headingB)−yshift⋅cos(headingB)∣
(2)代码中std::abs(dx1 * box.sin_heading() - dy1 * box.cos_heading())所表示的是向量
v
1
⃗
\vec{v_1}
v1在B的横轴上投影的模
a
1
a1
a1,结合公式(2)可知:
a
1
=
∣
v
1
⃗
⋅
(
sin
(
h
e
a
d
i
n
g
B
)
,
−
cos
(
h
e
a
d
i
n
g
B
)
)
∣
=
∣
d
x
1
⋅
sin
(
h
e
a
d
i
n
g
B
)
−
d
y
1
⋅
cos
(
h
e
a
d
i
n
g
B
)
∣
a1=|\vec{v_1}\cdot(\sin(heading_B),-\cos(heading_B))|=|dx1\cdot\sin(heading_B)-dy1\cdot\cos(heading_B)|
a1=∣v1⋅(sin(headingB),−cos(headingB))∣=∣dx1⋅sin(headingB)−dy1⋅cos(headingB)∣
代码中std::abs(dx2 * box.sin_heading() - dy2 * box.cos_heading())所表示的是向量
v
2
⃗
\vec{v_2}
v2在B的横轴上投影的模
a
2
a2
a2,结合公式(3)可知:
a
2
=
∣
v
2
⃗
⋅
(
sin
(
h
e
a
d
i
n
g
B
)
,
−
cos
(
h
e
a
d
i
n
g
B
)
)
∣
=
∣
d
x
2
⋅
sin
(
h
e
a
d
i
n
g
B
)
−
d
y
2
⋅
cos
(
h
e
a
d
i
n
g
B
)
∣
a2=|\vec{v_2}\cdot(\sin(heading_B),-\cos(heading_B))|=|dx2\cdot\sin(heading_B)-dy2\cdot\cos(heading_B)|
a2=∣v2⋅(sin(headingB),−cos(headingB))∣=∣dx2⋅sin(headingB)−dy2⋅cos(headingB)∣
由上图可知:
a
=
a
1
+
a
2
a=a1+a2
a=a1+a2
(3)代码中half_width是向量
v
4
⃗
\vec{v_4}
v4在其横轴上的投影的模,另外,向量
v
3
⃗
\vec{v_3}
v3此时在其横轴上投影的模为0。
c
1
=
a
+
w
i
d
t
h
h
a
l
f
c1=a+width_{half}
c1=a+widthhalf
若步骤f3~f6均满足 c < = c 1 c<=c1 c<=c1,则可判定两个Box存在碰撞(具体原理可参考OBB原理)。文章来源:https://www.toymoban.com/news/detail-624622.html
参考
[1] Apollo中Lattice轨迹碰撞检测
[2]自动驾驶运动规划中的碰撞检测文章来源地址https://www.toymoban.com/news/detail-624622.html
到了这里,关于百度Apollo规划算法——OBB障碍物检测代码解析的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!