[动态规划第一节]背包问题汇总

这篇具有很好参考价值的文章主要介绍了[动态规划第一节]背包问题汇总。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

背包问题

动态规划思路：
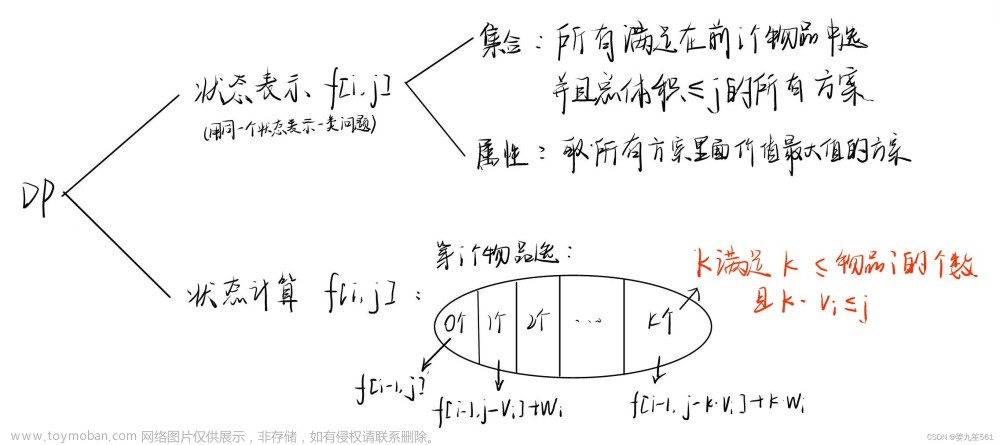
- 状态表示 f(i, j)
  - 状态由几维表示
    - 表示的集合是什么
      - 所有选法
      - 选法条件
        
        只考虑前i个物品
        
        总体积 <= j
    - 集合的属性是什么
      - 最大值
      - 最小值
      - 元素的数量
- 状态计算
  - 集合的划分 f(i, j)
    - 不含第i个物品
      - f(i - 1, j)
    - 包含第i个物品
      - f(i - 1, j - vi) 已知第i个物品必选，那么只要保证前i-1个物品为最大值

01背包

每件物品最多取一次

朴素代码：

const int N = 1e3 + 10;
int f[N][N], v[N], w[N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
    
    //f[1~n][0] = f[0][1~m] = 0;
    for(int i = 1; i <= n; ++ i) //遍历物品
        for(int j = 1; j <= m; ++ j){ //遍历容量
            f[i][j] = f[i - 1][j]; //不选第i个物品
            if(j >= v[i])
                f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]); //选第i个物品
        }
        
    cout << f[n][m];
    return 0;
}

优化：
- 用滚动数组优化
- 因为第i层总是由第i-1层来更新，不会用到1~i-2层，因此只用一维数组f[N]即可自我更新,f[j]表示不超过容量j的最大价值
- 第i个物品不取，第i层与第i-1层的总价值不变，因此可以不用更新，\(f[i][j] = f[i - 1][j]\) 这句话可删去
- 第i个物品取，因此要用i-1层更新第i层，\(f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i])\) 并且总是用小容量的价值更新大容量的价值，若从小往大更新，那么小容量的价值优先被更新到第i层，大容量的价值依据小容量的价值更新时，使用的价值不再是第i-1层，所以容量要从大往小更新
- 代码：
```
const int N = 1e3 + 10;
int f[N], v[N], w[N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
    
    //f[0] = 0;
    for(int i = 1; i <= n; ++ i) //遍历物品
        for(int j = m; j >= v[i]; -- j) //从小往大遍历容量
                f[j] = max(f[j], f[j - v[i]] + w[i]); //选第i个物品
        
    cout << f[m];
    return 0;
}
```

完全背包

每件物品可取无限次

朴素代码：

const int N = 1e3 + 10;
int f[N][N], w[N], v[N];
int n, m;

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; ++ i) //遍历物品
        for(int j = 1; j <= m; ++ j) //遍历容量
            for(int k = 0; k * v[i] <= j; ++ k) //遍历个数 
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                
    cout << f[n][m];
    return 0;
}

时间优化：

\(f[i][j] = max(f[i - 1][j],f[i - 1][j - v] + w,f[i-1][j-2v]+2w,f[i-1][j-3v]+3w,...,f[i-1][j-kv]+kw)\)
\(f[i][j-v]=max(f[i-1][j-v],f[i-1][j-2v]+w,f[i-1][j-3v]+w,...,f[i-1][j-kv]+(k-1)w,f[i-1][j-(k+1)v]+kw)\)
发现: \(f[i][j]=max(f[i-1][j],f[i][j-v]+w)\)

代码：

const int N = 1e3 + 10;
int f[N][N], w[N], v[N];
int n, m;

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; ++ i) //遍历物品
        for(int j = 1; j <= m; ++ j){ //遍历容量
            f[i][j] = f[i - 1][j]; //第i个物品不选
            if(j >= v[i])
                f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);//第i个物品选
        }
                
    cout << f[n][m];
    return 0;
}

时空优化：

滚动数组优化

代码：

const int N = 1e3 + 10;
int f[N], w[N], v[N];
int n, m;

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
    
    for(int i = 1; i <= n; ++ i) //遍历物品
        for(int j = v[i]; j <= m; ++ j) //遍历容量
            f[j] = max(f[j], f[j - v[i]] + w[i]);
                
    cout << f[m];
    return 0;
}

多重背包

每件物品可取有限次

朴素代码：

const int N = 110;
int f[N][N], v[N], w[N], s[N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1; i <= n; ++ i)
        for(int j = 1; j <= m; ++ j)
            for(int k = 0; k <= s[i] && k * v[i] <= j; ++ k)
                f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                
    cout << f[n][m];
    return 0;
}

空间优化：

滚动数组优化

代码：

const int N = 110;
int f[N], v[N], w[N], s[N];
int n, m;

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
    
    for(int i = 1; i <= n; ++ i)
        for(int j = m; j >= v[i]; -- j)
            for(int k = 0; k <= s[i] && k * v[i] <= j; ++ k)
                f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
                
    cout << f[m];
    return 0;
}

二进制优化：

将每个物品取的次数分为若干组，各组为1，2，4，8....2^k，c 的二进制数，在组中任意选取若干组，每组看作新的物品只能选一次，所有的次数都能由这几组二进制数表示，由于每组只能选一次，故化为01背包问题

代码：

const int N = 2e4 + 500;
int v[N], w[N], s[N];
int f[N];
int n, m;

int main(){
    cin >> n >> m;
    
    int cnt = 0; //记录物品个数
    while(n -- ){
        int V, W, S;
        cin >> V >> W >> S;
        int k = 1; //记录分解后每个物品的次数
        while(k <= S){ //将数量S分解
            cnt ++ ; //每次分解个数加一
            w[cnt] = W * k;
            v[cnt] = V * k;
            S -= k;
            k *= 2;
        }
        if(S > 0){ //剩余次数
            cnt ++ ;
            w[cnt] = W * S;
            v[cnt] = V * S;
        }
    }
    
    n = cnt; //01背包问题
    for(int i = 1; i <= n; ++ i)
        for(int j = m; j >= v[i]; -- j)
            f[j] = max(f[j], f[j - v[i]] + w[i]);
            
    cout << f[m];
    return 0;
}

分组背包

每个组里面最多选一件物品

朴素代码：

const int N = 110;
int v[N][N], w[N][N];
int f[N][N];
int s[N];
int n, m;

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; ++ i){
        cin >> s[i];
        for(int j = 1; j <= s[i]; ++ j)
            cin >> v[i][j] >> w[i][j];
    }
    
    for(int i = 1; i <= n; ++ i)
        for(int j = 1; j <= m; ++ j){
            f[i][j] = f[i - 1][j]; //该组不选物品
            for(int k = 1; k <= s[i]; ++ k){ //该组选物品
                if(j >= v[i][k])
                    f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
            }
        }
        
                
    cout << f[n][m];
    return 0;
}

//或者
for(int i = 1; i <= n; ++ i)
	for(int k = 1; k <= s[i]; ++ k)
		for(int j = 1; j <= m; ++ j){
			f[i][j] = max(f[i][j], f[i - 1][j]);
			if(j >= v[i][k])
				f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
		}

空间优化：

const int N = 110;
int v[N][N], w[N][N];
int f[N];
int s[N];
int n, m;

int main(){
    cin >> n >> m;
    
    for(int i = 1; i <= n; ++ i){
        cin >> s[i];
        for(int j = 1; j <= s[i]; ++ j)
            cin >> v[i][j] >> w[i][j];
    }
    
    for(int i = 1; i <= n; ++ i)
        for(int j = m; j >= 1; -- j)
            for(int k = 1; k <= s[i]; ++ k)
                if(j >= v[i][k])
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);
            
                
    cout << f[m];
    return 0;
}

文章来源地址https://www.toymoban.com/news/detail-647149.html

到了这里，关于[动态规划第一节]背包问题汇总的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！