动态规划之背包问题（全）

这篇具有很好参考价值的文章主要介绍了动态规划之背包问题（全）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

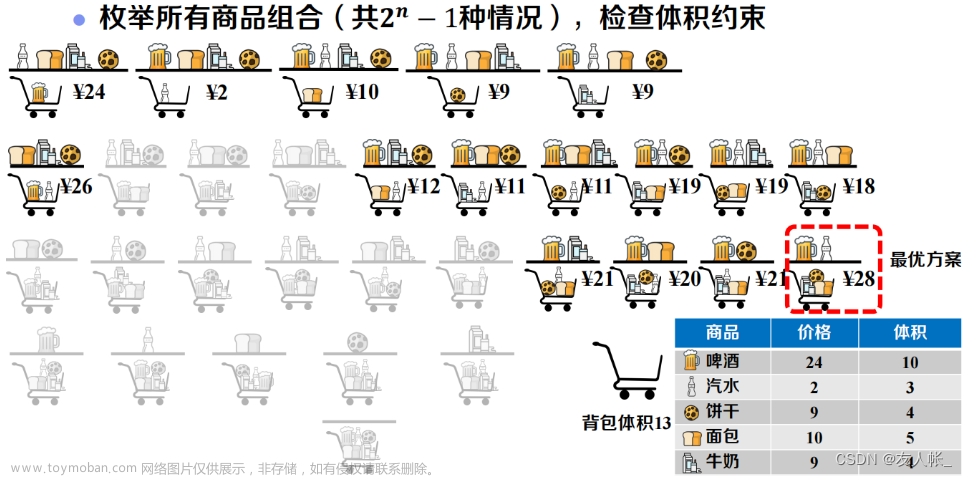
01背包问题

1.题目

有 N件物品和一个容量为 V的背包，每件物品有各自的价值且只能被选择一次，要求在有限的背包容量下，装入的物品总价值最大。

「0-1 背包」是较为简单的动态规划问题，也是其余背包问题的基础。

动态规划是不断决策求最优解的过程，「0-1 背包」即是不断对第 i 个物品的做出决策，「0-1」正好代表不选与选两种决定。

2.题解代码

2.1版本1 二维

动态规划背包问题,动态规划,java,动态规划,算法,Powered by 金山文档

（1）状态f[i][j]定义：只从前i个物品选，且选取物品总体积不超过j的最大价值

（2）状态计算（如何求f[i][j]）：将f[i][j]看作集合，划分为不包含第i个物品和包含第i个物品两类，不包含第i个物品为从前i-1个物品选，总体积不超过j所构成的集合，取最大值，即f[i-1][j]，包含第i个物品为从前i-1个物品选，总体积不超过j-vi的集合，取最大值然后加上选取物品i的权重，即f[i-1][j-vi]+wi；最后在两者之间选取最大值，即可求得f[i][j]。

（3）考虑背包容量是否大于物品i的体积:

j<v[i]: 无需考虑选取第i个物品的情况，对应代码：f[i][j] = f[i - 1][j]

j>=v[i]：选取和不选取第i个物品都得考虑，对应代码：Math.max(f[i - 1][j], f[i - 1][j - v[i]] + w[i])

代码如下：

import java.util.Scanner;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[][] f = new int[n + 1][m + 1];
        int[] v = new int[n + 1];
        int[] w = new int[n + 1];
        for (int i = 1; i <= n; i ++){
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }
        for (int i = 1; i <= n; i ++) {
            for (int j = 0; j <= m; j ++) {
                f[i][j] = f[i-1][j];
                if (v[i] <= j){
                    f[i][j] = Math.max(f[i-1][j], f[i-1][j-v[i]] + w[i]);
                }
            }
        }
        System.out.println(f[n][m]);
    }
}

2.2版本2 一维

将状态f[i][j]优化为以为f[j], 实际上只需要做一个等价变形。

由f[i][j] = Math.max(f[i-1][j], f[i-1][j-v[i]] + w[i])我们可知，我们每次求取f[i][j]的时候，都只用到了第i-1层的数据，而且题目只需要求得最总状态f[n][m],中间状态不需要存储。，所以我们每次求第i层的数据时只需要将第i-1层的数据覆盖即可。但是注意小细节，此时在一维情况下枚举背包容量时，需要逆序遍历，因为f[j-v[i]]在f[j]的左边，如果正序遍历的话，我们用到的数据就不是第i-1层的数据了，而是刚更新过的第i层数据。

import java.util.Scanner;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[] f = new int[m + 1];
        int[] v = new int[n + 1];
        int[] w = new int[n + 1];
        for (int i = 1; i <= n; i ++){
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }
        for (int i = 1; i <= n; i ++) {
            for (int j = m; j >= v[i]; j --) {
                f[j] = Math.max(f[j], f[j-v[i]] + w[i]);
            }
        }
        System.out.println(f[m]);
    }
}

完全背包问题

1.题目

有 N种物品和一个容量是 V 的背包，每种物品都有无限件可用。

第 i 种物品的体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。

输出最大价值。

2.题解代码

2.1简单版

（1）状态f[i][j]定义：只从前i个物品选，且选取物品总体积不超过j的最大价值

（2）状态计算：将集合f[i][j]划分为分别选取0~k个物品i，再对选取物品i的个数进行枚举，限制条件为k * v[i] <= j, 然后求最大值即可。

基本代码如下：

import java.util.Scanner;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[] v = new int[n+1];
        int[] w = new int[n+1];
        int[][] f = new int[n+1][m+1];
        for (int i = 1; i <= n; i ++) {
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }
        for (int i = 1; i <= n; i ++) {
            for (int j = 0; j <= m; j ++) {
                for (int k = 0; k * v[i] <= j; k ++) {
                    f[i][j] = Math.max(f[i][j], f[i-1][j-k*v[i]] + k*w[i]);
                }
            }
        }
        System.out.println(f[n][m]);
    }
}

2.2优化版

优化思路：

f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)

f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)

由上两式，可得出如下递推关系：

f[i][j]=max(f[i,j-v]+w , f[i-1][j])

有了上面的关系，那么其实k循环可以不要了，核心代码优化成这样：

for(int i = 1 ; i <=n ;i++)
    for(int j = 0 ; j <=m ;j++)
    {
        f[i][j] = f[i-1][j];
        if(j-v[i]>=0)
            f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
    }

这个代码和01背包的非优化写法很像啊!!!我们对比一下，下面是01背包的核心代码

for(int i = 1 ; i <= n ; i++)
    for(int j = 0 ; j <= m ; j ++)
    {
        f[i][j] = f[i-1][j];
        if(j-v[i]>=0)
            f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);
    }

两个代码其实只有一句不同（注意下标）

f[i][j] = max(f[i][j],f[i-1][j-v[i]]+w[i]);//01背包

f[i][j] = max(f[i][j],f[i][j-v[i]]+w[i]);//完全背包问题

综上所述，完全背包的最终写法如下：

import java.util.Scanner;

public class Main{
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[] v = new int[n+1];
        int[] w = new int[n+1];
        int[] f = new int[m+1];
        for (int i = 1; i <= n; i ++) {
            v[i] = sc.nextInt();
            w[i] = sc.nextInt();
        }
        for (int i = 1; i <= n; i ++) {
            for (int j = v[i]; j <= m; j ++) {
                f[j] = Math.max(f[j], f[j-v[i]] + w[i]);
            }
        }
        System.out.println(f[m]);
    }
}

多重背包问题（二进制优化）

1.题目

有 N种物品和一个容量是 V的背包。

第 i种物品最多有 si件，每件体积是 vi，价值是 wi。

求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。

输出最大价值。

2.解题代码

多重背包问题简单版和完全背包问题简单版是相同的解题思路，这里直接上优化版

在完全背包中,通过两个状态转移方程：

f[i,j]=max(f[i−1,j],f[i−1,j−v]+w,f[i−1,j−2v]+2w,f[i−1,j−3v]+3w,.....)

f[i,j−v]=max(f[i−1,j−v],f[i−1,j−2v]+w,f[i−1,j−2v]+2w,.....)

通过上述比较，可以得到f[i][j] = max(f[i-1][j],f[i][j-v]+w)

再来看下多重背包,

f[i,j] = max(f[i−1,j],f[i−1,j−v]+w,f[i−1,j−2v]+2w,.....f[i−1,j−Sv]+Sw,)

f[i,j-v] = max(f[i−1,j−v],f[i−1,j−2v]+w,.....f[i−1,j−Sv]+(S−1)w,f[i−1,j−(S+1)v]+Sw)

这里比完全背包方程多了一项，不能像完全背包一样去优化

二进制优化思路：

将每一组拥有的个数进行二进制计算，使每组进行二进制分割之后变为01背包问题，即假设有1023个；二进制的思维，将1023按照1，2，4，8，16，... ，512分到10个箱子里，根据数学知识，如何一个我们需要拿的数字x∈[0,1023]都可以用这10个箱子里的苹果数量表示出来，这样的话时间复杂度从O(n3)降到O(n2logS)

import java.util.Scanner;

public class Main{
    static int N = 12010;//逐一枚举最大是N*logS
    
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[] v = new int[N];
        int[] w = new int[N];
        int[] f = new int[m+1];
        int cnt = 0;
        for (int i = 1; i <= n; i ++) {
            int a = sc.nextInt();
            int b = sc.nextInt();
            int s = sc.nextInt();
            int k = 1;
            while(k <= s) {
                cnt ++;
                v[cnt] = a * k; //整体体积
                w[cnt] = b * k; // 整体价值
                s -= k; // s要减小
                k *= 2; // 组别里的个数增加
            }
            if (s > 0) {
                cnt ++;
                v[cnt] = a * s;
                w[cnt] = b * s;
            }
        }
        n = cnt;//枚举次数由个数变成组别数
        //01背包一维优化
        for (int i = 1; i <= n; i ++) {
            for (int j = m; j >= v[i]; j --) {
                f[j] = Math.max(f[j], f[j-v[i]] + w[i]);
            }
        }
        System.out.println(f[m]);
    }
}

分组背包问题

题目

有 N组物品和一个容量是 V的背包。

每组物品有若干个，同一组内的物品最多只能选一个。

每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。

求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。

输出最大价值。

2.题解代码

（1）状态f[i][j]定义：只从前i组物品选，且选取物品总体积不超过j的最大价值

（2）状态计算（如何求f[i][j]）：将f[i][j]看作集合，划分为不包含第i组的物品和包含第i组的第k个物品两类，不包含第i组的物品为从前i-1组物品选，总体积不超过j所构成的集合，取最大值，即f[i-1][j]，包含第i组的第k个物品为从前i-1个物品选，总体积不超过j-v[i,k]的集合，取最大值然后加上选取第i组物品的第k个物品的权重，即f[i-1][j-v[i,k]]+w[i,k]；最后在两者之间选取最大值，即可求得f[i][j]。

代码如下：

import java.util.Scanner;

public class Main{
    static int N = 110;
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[][] v = new int[n+1][N];
        int[][] w = new int[n+1][N];
        int[] s = new int[n+1];
        int[][] f = new int[n+1][m+1];
        for (int i = 1; i <= n; i ++) {
            s[i] = sc.nextInt();
            for (int j = 1; j <= s[i]; j ++) {
                v[i][j] = sc.nextInt();
                w[i][j] = sc.nextInt();
            }
        }
        
        for (int i = 1; i <= n; i ++) {
            for (int j = 0; j <= m; j ++) {
                f[i][j] = f[i-1][j];
                for (int k = 0; k <= s[i]; k ++) {
                    if (j >= v[i][k]){
                        f[i][j] = Math.max(f[i][j], f[i-1][j-v[i][k]] + w[i][k]);   
                    }
                }
            }
        }
        System.out.println(f[n][m]);
    }
}

因为只用到了第i-1列，所以可以仿照01背包的套路逆向枚举体积文章来源地址https://www.toymoban.com/news/detail-662292.html

import java.util.Scanner;

public class Main{
    static int N = 110;
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int n = sc.nextInt();
        int m = sc.nextInt();
        int[][] v = new int[n+1][N];
        int[][] w = new int[n+1][N];
        int[] s = new int[n+1];
        int[] f = new int[m+1];
        for (int i = 1; i <= n; i ++) {
            s[i] = sc.nextInt();
            for (int j = 1; j <= s[i]; j ++) {
                v[i][j] = sc.nextInt();
                w[i][j] = sc.nextInt();
            }
        }
        
        for (int i = 1; i <= n; i ++) {
            for (int j = m; j >= 0; j --) {
                for (int k = 1; k <= s[i]; k ++) {
                    if (j >= v[i][k]){
                        f[j] = Math.max(f[j], f[j-v[i][k]] + w[i][k]);   
                    }
                }
            }
        }
        System.out.println(f[m]);
    }
}

到了这里，关于动态规划之背包问题（全）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！