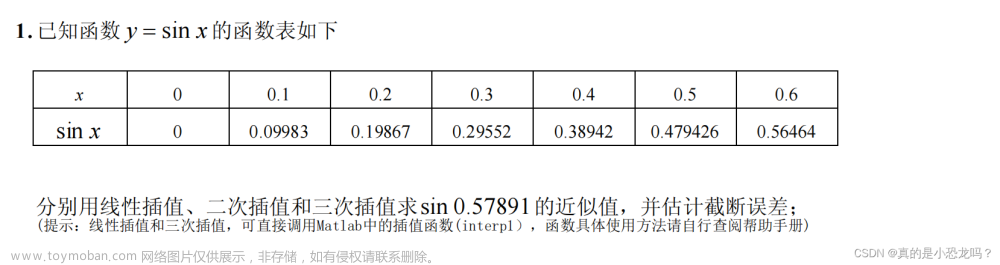
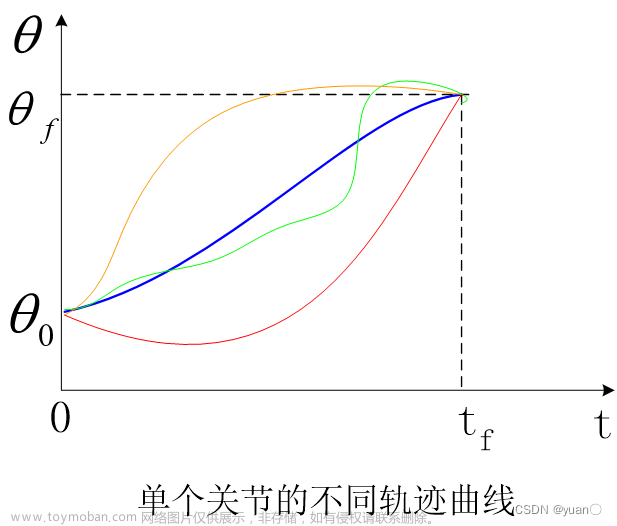
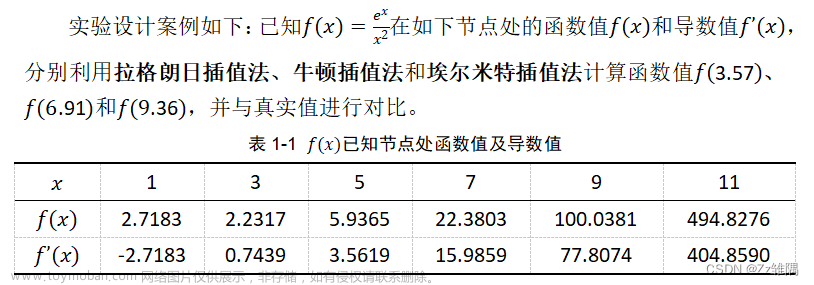
插值：数据处理的手段 将缺失数据补全处理 线性内插 拉格朗日插值法 牛顿插值
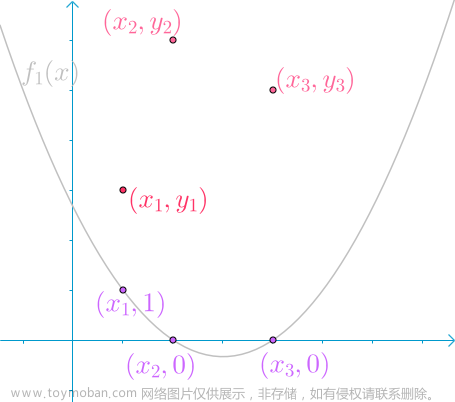
拟合：预测，寻找规律的手段 是插值的外延
插值算法：使用在现有的数据极少，不足以支撑分析的进行，这时就需要使用一些数学方法来“模拟产生”一些新的但又比较靠谱的值来满足需求。
适用在“已知函数在某区间（域）内若干点处的值，求函数在该区间（域）内其他点处的值”
一维插值问题：
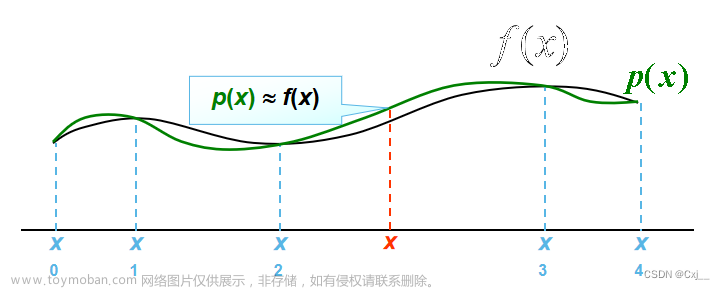
插值法概念：
一般定义：1.若P(x)是次数不差过n的代数多项式，即
2.若P(x)为分段多项式（分段函数），就称为分段插值。（出现较多 ）
3.若P(x)为三角多项式，就称为三角插值。（涉及傅里叶变换等数学）
一般插值法原理：
定理：设有n+1个互不相同的结点（xi，yi）（i=0,1,2,......n）则存在唯一的多项式：
证：将n+1个结点带入上式构造方程组
文章来源地址https://www.toymoban.com/news/detail-687366.html
【注1】只要n+1个节点互异，满足上述插值条件的多项式是唯一存在的；次数已经限定
【注2】如果不限制多项式的次数，插值多项式并不唯一
拉格朗日插值法：
缺点：产生龙格现象 次数越高误差越大 在实际应用中不应使用七次以上的插值
避免龙格现象常用方法：将插值区间分成若干小区间，在小区间内用低次（二次，三次）插值，即分段低次插值，如样条函数插值
牛顿插值法 ：
与拉格朗日插值法比，牛顿插值法的计算过程具有继承性，但仍会有龙格现象，并且都不能全面反映被插函数的性态。
分段三次埃尔米特（Hermite）插值法：
Matlab有内置函数：p=pchip(x,y,new_x) x是已知样本点的横坐标；y是已知样本点的纵坐标；new_x是要插入对应的横坐标
例如:
X=-pi:pi;y=sin(x);
New_X=-pi:0.1:pi;
p=pchip(x,y,new_x) ;
Plot(x,y,’o’,new_x,p,’r-’)
Plot3空间曲线，mesh（空间曲面 曲面网格），surf（空间曲面 曲面表面），contour（等高线）是三维作图中的命令
三次样条插值：（推荐）
Matlab有内置函数：p=spine(x,y,new_x)
Legend(“string1”,”string2”,”string3”),内加‘Location：’改变标注的位置
n维数据插值：
P=interpn（x1，....xn，y,new_x1,...new_xn,method）
Method:’linear：线性插值（默认）‘cubic’：三次插值 ‘spine’=三次样条插值法（最为标准） ‘nearest’：最邻近插值算法
一个小技巧：上面的这些插值算法可用于预测哦~~~
分享：
“她哪里是想考研啊，她只是想再回到高三完成十八岁那未完成的梦罢了。”
--2022.12.23 祝考研的学长学姐“一研为定，定为研一”
文章来源：https://www.toymoban.com/news/detail-687366.html
到了这里，关于插值算法基本原理的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
