Python矩阵LU分解

这篇具有很好参考价值的文章主要介绍了Python矩阵LU分解。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

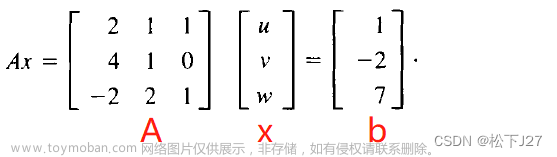
scipy.linalg中提供了一系列矩阵分解函数，其中最基础的肯定是LU分解。

L和U

LU分解，即使得矩阵 $A$ 分解为 $LU$ ，其中 $L$ 为下三角阵， $U$ 为上三角阵。对于这两种矩阵，scipy.linalg中提供了tril, triu，可以将第 $k$ 条对角线下面或上面的所有元素置零，即可以此获取L矩阵或者U矩阵。

import numpy as np
import scipy.linalg as sl
x = np.random.rand(4,4)
print(sl.tril(x,-1))	# 返回见[1]

$\begin{bmatrix} 0.&0.&0.&0.\\ 0.62594216&0.&0.&0.\\ 0.16043717&0.5820587&0.&0.\\ 0.24560828&0.76599572&0.1922379& 0.\\ \end{bmatrix}$

print(sl.triu(x,2))		#

$\begin{bmatrix} 0.&0.&0.91943758&0.2531733 \\ 0.&0.&0.&0.76514452\\ 0.&0.&0.&0.\\ 0.&0.&0.&0. \end{bmatrix}$

lu分解

LU分解几乎是任何有关矩阵算法的书籍中，第一个出现的矩阵分解方法。在scipy.linalg中，提供了lu, lu_factor, lu_solve等函数，分别用于LU分解，以及通过LU分解求解Ax=b类似的问题。

LU分解示例如下

import numpy as np
from scipy.linalg import lu
A = np.random.rand(4,4)
p, l, u = lu(A)
np.allclose(A - p @ l @ u, np.zeros((4, 4)))
# True

lu函数除了a和用于有限性校验以及a可覆盖性的参数之外，还有一个permute_l，默认为False，当其为True时，将返回两个参数pl, u。其中pl==p@l。

lu_factor(a)以另一种形式返回LU分解的结果。其返回值有二，分别是lu, piv，其中LU就是 $L + U - I$ ，其中 $I$ 为单位阵；piv表示矩阵 $P$ 中不为零的元素的位置。

lu_solve

lu_solve是根据 $LU$ 分解求解 $P LUx - b$ 的问题，其输入为(lu, piv)和b，测试如下

>>> b = np.array([1,2,3,4])
>>> lu, pix = sl.lu_factor(A)
>>> x = lu_solve((lu, pix), b)
>>> A@x-b
array([ 2.22044605e-16, -4.44089210e-16,  0.00000000e+00,  0.00000000e+00])

其中A就是上面生成的随机矩阵，值为

$\begin{bmatrix} 0.2495995&0.59179571&0.34236803&0.78559552\\ 0.39427709&0.36015762&0.23789732&0.09223244\\ 0.79701282&0.40291763&0.93215531&0.10486747\\ 0.46812908&0.58426202&0.16560106&0.96889267 \end{bmatrix}$ 文章来源地址https://www.toymoban.com/news/detail-719112.html