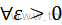1 二重积分换元法
二重积分换元公式（第七版同济书下册P152）
设
f
(
x
,
y
)
f(x, y)
f(x,y) 在
x
O
y
x O y
xOy 平面上的闭区域
D
D
D 上连续，若变换
T
:
x
=
x
(
u
,
v
)
,
y
=
y
(
u
,
v
)
T: x=x(u, v),\ y=y(u, v)
T:x=x(u,v), y=y(u,v)
将
u
O
v
u O v
uOv 平面上的闭区域
D
′
D^{\prime}
D′ 变为
x
O
y
x O y
xOy 平面上的
D
D
D，且满足
(1) x ( u , v ) , y ( u , v ) x(u, v), y(u, v) x(u,v),y(u,v) 在 D ′ D^{\prime} D′ 上具有一阶连续偏导数；
(2) 在
D
′
D^{\prime}
D′ 上雅可比式
J
(
u
,
v
)
=
∂
(
x
,
y
)
∂
(
u
,
v
)
≠
0
;
J(u, v)=\dfrac{\partial(x, y)}{\partial(u, v)} \neq 0 ;
J(u,v)=∂(u,v)∂(x,y)=0;
(3) 变换 T : D ′ → D T: D^{\prime} \rightarrow D T:D′→D 是一对一的，
则有
∬
D
f
(
x
,
y
)
d
x
d
y
=
∬
D
′
f
[
x
(
u
,
v
)
,
y
(
u
,
v
)
]
∣
J
(
u
,
v
)
∣
d
u
d
v
.
\iint\limits_D f(x, y) \mathrm{d}x \mathrm{d}y=\iint\limits_{D'} f[x(u, v), y(u, v)]~|J(u, v)|~\mathrm{d} u \mathrm{d} v .
D∬f(x,y)dxdy=D′∬f[x(u,v),y(u,v)] ∣J(u,v)∣ dudv.
示例：
2 概率论卷积公式
卷积公式（浙大书第五版P77）
一般方法证明（浙大书第五版P78）：
使用二重积分换元法来证明：
卷积公式的一般形式
文章来源：https://www.toymoban.com/news/detail-766316.html
参考：概率论～卷积公式文章来源地址https://www.toymoban.com/news/detail-766316.html
到了这里，关于从二重积分换元法到概率论卷积公式的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
