Matlab 优化工具箱

这篇具有很好参考价值的文章主要介绍了Matlab 优化工具箱。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1 线性规划

1.1 线性规划问题—linprog

语法：[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb,ub,options)
matlab优化工具箱,matlab,矩阵,开发语言,线性回归
f、x、b、beq、lb 和 ub 是向量，A 和 Aeq 是矩阵。
示例1-1：

f = [-5,-4,-6];
A = [1,-1,1;3,2,4;3,2,0];	%系数矩阵
b = [20,42,30];				%常数项
Aeq = []; beq = [];
lb=[0,0,0];ub = [];x0 = [];
[x,fval,exitflag,output,lambda] = linprog(f,A,b,Aeq,beq,lb,ub,x0);

1.2 混合整数线性规划(MILP)—linprog

语法：[x,fval,exitflag,output] = intlinprog(f,intcon,A,b,Aeq,beq,lb,ub,x0,options)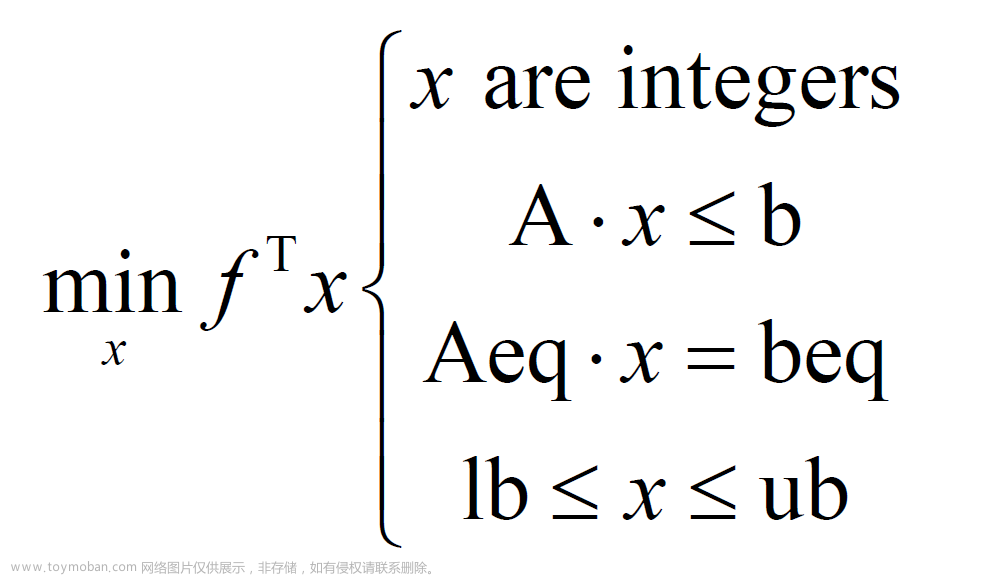
matlab优化工具箱,matlab,矩阵,开发语言,线性回归

f、x、intcon、b、beq、lb 和 ub 是向量，A 和 Aeq 是矩阵。

2 非线性规划

2.1 约束非线性多变量函数的最小值—fmincon()

语法：x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)

fmincon函数是默认从给定的x0为中心开始搜索，直至找到函数的z最小值，并返回距离x0最近的函数最小值对应的值,在计算的时候就必须预先判定函数最小值的对应的x值的大概范围,确保定的初值x0在所求的x附近，以减少计算量。

fmincon求解优化问题，最优解不一定唯一。选择不同的迭代初始值x0，可能得到不同的局部最优解(局部最优解不一定为全局最优解)

clc; close all; clear; % 寻找约束非线性多变量函数的最小值
fun = @(x)x;    % 目标函数
x0=[];          % 初始值， length(x0) = 自变量个数, 从x0开始
A=[];           % 系数矩阵 A*x <= b
b=[];           % 向量
Aeq=[];         % 系数矩阵 Aeq*x = beq
beq=[];         % 向量
lb=[];          % 自变量约束边界 lb(1) <= x(1) <= ub(1)        lb(2) <= x(2) <= ub(2)
ub=[];          % 如果 x(i) 无下界，请设置 lb(i) = -Inf，如果 x(i) 无上界，请设置 ub(i) = Inf。
nonlcon = [];         % 非线性约束
option=[];			  %options = optimset('Display','iter');   %在每次迭代时显示输出
[x,f]=fmincon(fun ,x0,A,b,Aeq,beq,lb,ub,nonlcon,option);

示例1：求解有约束最优化问题（常规—线性约束函数）
matlab优化工具箱,matlab,矩阵,开发语言,线性回归

fun = @(x)-(x(2)+x(1)*cos(x(3)))*x(1)*sin(x(3));  % 目标函数
x0=[25;20;1];          % 初始值， length(x0) = 自变量个数, 从x0开始
A=[]; b=[];           
Aeq=[2,1,0];  beq=100;     
lb=[0;0;0];  ub=[100;100;pi/2];  % 自变量约束边界 lb(1) <= x(1) <= ub(1)  lb(2) <= x(2) <= ub(2)         
[x,f]=fmincon(fun ,x0,A,b,Aeq,beq,lb,ub);

示例2-1：求解有约束最优化问题（难—单个非线性约束函数）
matlab优化工具箱,matlab,矩阵,开发语言,线性回归
【步骤1】：定义非线性约束函数

function [c, ceq] = WT_1_non(x)
c=9-x(1)^2-x(2)^2;  %定义非线性约束函数， C*x <= 0;
ceq=[];				%Ceq*x=0;

【步骤2】：定义目标函数

fun = @(x) x(1)^4-4*x(1)-8*x(2)+15;  %定义目标函数
nonlcon = @(x)WT_1_non(x);            %定义非线性约束函数，@WT_1_non
A=[2 3;-1,1];
b=[2;5];
[x,fval]=fmincon(fun,[0,1],A,b,[],[],[],[],nonlcon);

示例2-2：求解有约束最优化问题（难—多个非线性约束函数）
matlab优化工具箱,matlab,矩阵,开发语言,线性回归
【步骤1】：定义非线性约束函数

function [c, ceq] = fun_constraint(x)
c=[3+x(1)*x(2)-x(1)-x(2);x(1)*x(2)-12];
ceq=[];

【步骤2】：定义目标函数

fun = @(x)exp(x(1))*(x(1)^2+2*x(2)^2+3*x(1)*x(2)+5*x(1)+4*x(2)+2);  % 目标函数
fun_con = @fun_constraint;          %非线性约束函数
x0=[-1,1];          % 初始值， length(x0) = 自变量个数, 从x0开始
A=[]; b=[];           
Aeq=[1,2];  beq=0;       
lb=[];  ub=[];  % 自变量约束边界 lb(1) <= x(1) <= ub(1)  lb(2) <= x(2) <= ub(2)         
[x,f]=fmincon(fun ,x0,A,b,Aeq,beq,lb,ub,fun_con);

示例2-3：求解有约束最优化问题（难—多个非线性约束函数）
matlab优化工具箱,matlab,矩阵,开发语言,线性回归
将问题模型转化为标准形式

【步骤1】：定义非线性约束函数

function [c, ceq] = fun_constraint(x)
c=[x(1)^2*x(2)-675;x(1)^2*x(3)^2/10^7-0.419];
ceq=[];

【步骤2】：定义目标函数

fun = @(x)-0.201*x(1)^4*x(2)*x(3)^2/10^7;  % 目标函数
fun_con = @fun_constraint;          %非线性约束函数
x0=[4;5;50];          % 初始值， length(x0) = 自变量个数, 从x0开始
A=[]; b=[];           
Aeq=[];  beq=[];       
lb=[0;0;0];  ub=[36;5;125];  % 自变量约束边界 lb(1) <= x(1) <= ub(1)  lb(2) <= x(2) <= ub(2)         
[x,f]=fmincon(fun ,x0,A,b,Aeq,beq,lb,ub,fun_con);

示例3：将梯度计算加入目标函数中，以实现更快或更可靠的计算。
matlab优化工具箱,matlab,矩阵,开发语言,线性回归
【步骤1】：定义梯度函数

function [f,g] = Learn_C_Ti(x)
f = 100*(x(2) - x(1)^2)^2 + (1-x(1))^2;% Calculate objective f
if nargout > 1      % gradient required
    g = [-400*(x(2)-x(1)^2)*x(1)-2*(1-x(1));
        200*(x(2)-x(1)^2)];
end

【步骤2】：定义目标函数

options = optimoptions('fmincon','SpecifyObjectiveGradient',true);%创建使用目标函数梯度的选项。
fun = @Learn_C_Ti;
x0 = [-1,2];
A = [];b = [];
Aeq = [];beq = [];
lb = [-2,-2];ub = [2,2];
nonlcon = [];
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options);

2.2 求解半无限约束多变量非线性函数的最小值 —fseminf()

语法：x = fseminf(fun,x0,ntheta,seminfcon,A,b,Aeq,beq,lb,ub,options)

2.3 寻找能够最小化一组目标函数最大值的点—fminimax()

语法：x = fminimax(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
示例：求解函数组取极小-极大值时X的值。
matlab优化工具箱,matlab,矩阵,开发语言,线性回归

【步骤1】：定义非线性约束函数

function f = fun7(x)
f = [2*x(1)^2+x(2)^2-48*x(1)-40*x(2)+304
    -x(1)^2 - 3*x(2)^2
    x(1)+3*x(2)-18
    -x(1)-x(2)
    x(1)+x(2)-8];

【步骤2】：定义主函数

clc,clear
[x,y] = fminimax(@fun7,rand(2,1))

2.4 无导数法计算无约束多变量函数的最小值—fminsearch()

语法：x = fminsearch(fun,x0,options)
示例：
matlab优化工具箱,matlab,矩阵,开发语言,线性回归

fun = @(x)100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;	%函数
x0 = [-1.2,1];		%自变量区间
options = optimset('Display','iter');   %在每次迭代时显示输出
x = fminsearch(fun,x0,options)

fminsearch函数是求解多元函数最小值，需给定初值x0，它采用复形搜索法;

2.5 其他

x = fminbnd(fun,x1,x2) %查找单变量函数在定区间上的最小值, 区间[x1,x2]

fun = @(x)(x^3+cos(x)+x*log(x))/exp(x);
[x,fval]=fminbnd(fun,0,2);

总结：fminbnd函数是针对于一元函数求最小值的函数，它是采用的黄金分割法和抛物线插值法，只能求一元连续函数在闭区间上的极值，有时只能求局部极值，若在边界达到极值，求解速度较慢;

x = fminunc(fun,x0,options)%求无约束多变量函数的最小值
示例：

fun=@(x)x(1)^3+x(2)^3-3*x(1)*x(2);
[x,fval]=fminunc(fun,[0.5,3]);

fminunc与fminsearch类似，它采用大规模内点反射牛顿迭代法或中小规模的拟牛顿法，速度快于fminsearch；故对于求解极值问题可以优先考虑使用fminunc函数.

当目标函数阶数大于2时，fminunc()比fminsearch()更有效；当目标函数高度不连续时，fminsearch()更具稳健性。

3 二次规划—quadprog()

语法：x = quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options)

示例1：
matlab优化工具箱,matlab,矩阵,开发语言,线性回归
将二次规划转化为标准形式：

H=[4,-1;-1,2];f=[-3;-5];
A=[1,1;-1,2];b=[5;4];
Aeq=[];         % 系数矩阵 Aeq*x = beq
beq=[];         % 向量
lb=[0;0];ub =[];x0 =[];
options = optimset('Display','iter');   %在每次迭代时显示输出
[x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options);

示例2：
matlab优化工具箱,matlab,矩阵,开发语言,线性回归
将二次规划转化为标准形式：
文章来源地址https://www.toymoban.com/news/detail-784918.html

H=[2,1,1;1,2,0;1,0,2];f=[-5;-3;-6];
A=[5,4,7];b=22;
Aeq=[];         % 系数矩阵 Aeq*x = beq
beq=[];         % 向量
lb=[0;0;0];ub =[];x0 =[];
options = optimset('Display','iter');   %在每次迭代时显示输出
[x,fval]=quadprog(H,f,A,b,Aeq,beq,lb,ub,x0,options);

到了这里，关于Matlab 优化工具箱的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！