一、拜耳阵列的来源
图像传感器将光线转化成电流，光线越亮，电流的数值就越大；光线越暗，电流的数值就越小。图像传感器只能感受光的强弱，无法感受光的波长。由于光的颜色由波长决定，所以图像传播器无法记录颜色，也就是说，它只能拍黑白照片，这肯定是不能接受的。
一种解决方案是照相机内置三个图像传感器，分别记录红、绿、蓝三种颜色，然后再将这三个值合并。这种方法能产生最准确的颜色信息，但是成本太高，无法投入实用。
1974年，柯达公司的工程师Bryce Bayer提出了一个全新方案，在图像传感器前面，设置一层彩色滤光片阵列（Color Filter Array，CFA） ，有间隔的在每个像素上放置单一颜色的滤镜。 这样，每个通道能得到一个部分值空缺的图片，然后通过各种插值手段填充空缺的值，进而得到彩色图像。
二、拜耳阵列的工作原理
拜耳阵列是实现CCD 或CMOS 传感器拍摄彩色图像的主要技术之一。它模拟人眼对色彩的敏感程度，采用1红2绿1蓝的彩色滤光片阵列，对光线进行过滤。
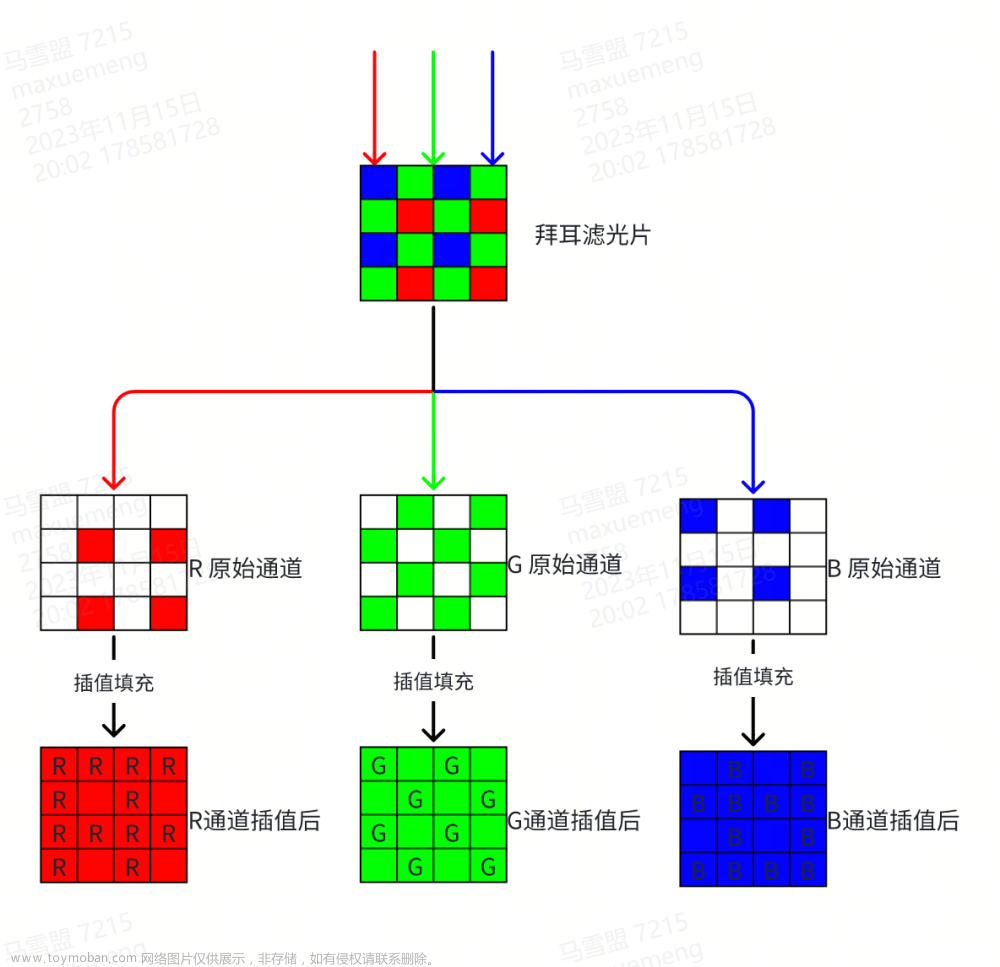
如下图所示，光线经过拜耳滤光片，获取到R、G、B三个通道的图像，R通道和B通道分别只有1/4的像素被填充，G通道只有1/2的像素被填充。通过插值算法，将R、G、B三个通道的原始图填充，就可以得到完备的彩色图像。
三、常见色彩滤波矩阵（CFA）
随着科技发展，越来越多不同设计的CFA被应用于相机和手机中。主要分为RGB、RGB-IR、RCCC、其它等四类。
3.1 For RGB sensor
在数字化的时代，需要一种标准来量化自然界的各种颜色。RGB就是一种在数字化领域表示颜色的标准，也称作一种色彩空间，通过用三原色R、G、B的不同的亮度值组合来表示某一种具体的颜色。注意，RGB里面存的是颜色的亮度值，而不是色度值。
RGB类型的色彩滤波矩阵，最常用，只包含R、G、B三个通道。根据不同排列，又可以下面RGGB、BGGR、GRBG和GBRG四类。 
3.2 For RGB-IR sensor
IR是Infrared，即红外线，其波长（约760nm~1mm）比红光长，是不可见光。在光线比较暗的情况下，使用IR摄像头增强现实效果。RGB-Ir技术使用RGB-Ir CFA，基于Bayer格式，修改部分像素点为IR像素点，而IR像素点只允许红外光通过。
RGB-Ir技术可以通过一个传感器设备同时捕捉到RGB彩图和IR图，也就是同时拥有白天和夜间的可视能力。根据各通道的位置不同，又可以细分成RGGI、IGGR、GRIG、GIRG、BGGI、IGGB、GBIG、GIBG八类。 
3.3 For RCCC sensor
RCCC就是CFA采用 Red-Monochrome配置，CFA滤波器结构中包括 3 个空白（Clear -C）和 1 个红光滤波器。75% 部分为透传，其余 25% 为感受红光的滤波器。RCCC 的优点是光灵敏度高，适用于弱光环境。由于 RCCC 只有红色光滤波器，因此主要用在对于红色标识敏感的场合，比如交通灯检测。根据R通道的位置不同，又可以分为RCCC、CCCR、CRCC、CCRC四类。
3.4 其它类型CFA
除了上面介绍的几类，还有很多其他的类别，如下图所示。在选择的时候，按需来。
一个专注于“嵌入式知识分享”、“DIY嵌入式产品”的技术开发人员，关注我，一起共创嵌入式联盟。文章来源：https://www.toymoban.com/news/detail-787233.html
文章来源地址https://www.toymoban.com/news/detail-787233.html
到了这里，关于拜耳阵列（Bayer Pattern）以及常见彩色滤波矩阵（CFA）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
