离散数学·图的矩阵表示、平面图

1年前作者：call me by ur name分类：Toy博客阅读(11)违法举报

这篇具有很好参考价值的文章主要介绍了离散数学·图的矩阵表示、平面图。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

有向图关联矩阵

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

无环，有向（可以表示平行边）
M(D)【direction】

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

每一列的和都是0，每一行中所有元素的绝对值是点的度数

性质

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

所有列相加一定是0（每一列都是0）
第i行第j列是1的情况的和是出度数
同1
平行边的表示就是再加一条一样的列

无向图关联矩阵

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

无向，无环
M(G)

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

性质

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

看一下（3）吧🎱🎱🎱

基本关联矩阵

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

简而言之——原矩阵删掉了一行就是基本关联矩阵
删掉的那一行应该是 1 最多的

无向图关联矩阵和基本关联矩阵的秩

矩阵的秩：化简之后的非零行的行数

基本关联矩阵和生成树

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

例

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

2，3，4指代的是e₂，e₃，e₄的导出子图

有向图的邻接矩阵

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

即为相邻（点与点是连通的）

性质

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

邻接矩阵和通路数

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法
回路看对角线
A²中的a₁₂表示从v₁到v₂长度为2的通路的数量2023.2.13复习
r表示长度
A^r矩阵表示的是长度为r的通路
B^r相当于是A¹+A²+……+Aⁿ，所以B^r表示的是通路长度≤r的通路

可达矩阵

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

就是2个点是连通的，矩阵相应位置就为1（注意是在有向图）
可达 —— 有向

性质

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

默认对角线元素全为1

无向图的相邻矩阵

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

性质

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

连通矩阵

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法
连通 —— 无向
不难看出，有向图的邻接矩阵、可达矩阵和无向图的相邻矩阵、连通矩阵是有很多相似的

平面图

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法
边与边不在非顶点处相交 —— K₄是可平面图，K₅不是

K₄平面图
离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

例

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法
不难看出，对于K₅或者K_3,3来说，在画图的时候，会发现，存在至少一个点是被周围的边包围起来的（这一页中紫色线指向的点靠近与其他边相交的地方，都是被周围的边无死角地包围起来了）

面和次

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

面的次数——边界的条数

例

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

悬挂边的次数是2——（那FE举例，内部区域为FECD）相当于从起点走到终点，F–E–C–D–E–F，通过这个轨迹可以看出FE这条边走了2次

定理

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

类似握手定理，没什么好说的

极大平面图

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

只用知道一下：极大平面图是连通的，每个区域的次数都为3
n≥3时，没有割点和桥2023.2.13复习

欧拉公式

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

连通

如果非连通——n-m+r=1+p
p为连通分支数

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法
不太需要背下来

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法
简单平面图， $l$ ≥ 32023.2.13复习
若为简单极大平面图——m=3n-6

Kuratowski定理

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法
拿K₅和K₃₃到图G中找2023.2.13复习

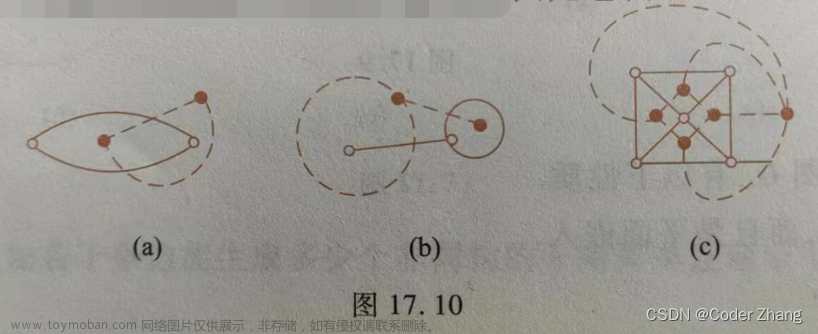
对偶图

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

这一页就图一乐🥙🥙🥙
用例子讲会好一些

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

每个区域在对偶图中变成一个点，如果存在区域与区域间共有的边界，那2个区域间连线（每有一条相应画一条线与之相交【图中虚线处】，悬挂边或桥就自身穿出和穿入）

性质

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

对偶图是连通的

作业

5

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

没什么难的🥪🥪🥪
但是，要知道定理：简单平面图，有m≤3n-6

6

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

虽然思维上没什么难度，但是要熟练掌握定理（特别是成立的条件）：

连通平面图，有n-m+r=2
简单平面图，有deg®≥3
任意平面图，都有∑deg®=2m

11 自对偶

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

同样没什么思维难度，但是要掌握相应知识点

自对偶：对偶图与原图同构（点、边的数量相同）
对偶图是连通的

12

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法

13

离散数学关系矩阵和关系图怎么画,矩阵,c++,算法
文章来源地址https://www.toymoban.com/news/detail-790675.html

到了这里，关于离散数学·图的矩阵表示、平面图的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：

领支付宝红包赞助服务器费用

离散数学复习---第十七章平面图【概念版】
目录 17.1 平面图的基本概念 17.2 欧拉公式 17.3 平面图的判断 17.4 平面图的对偶图定义17.1 如果能将无向图G画在平面上使得除顶点外处处无边相交，则称G为可平面图，简称为平面图。画出的无边相交的图称为G的平面嵌入。无平面嵌入的图称为非平面图。定理17.
2024年02月05日
浏览(12)
基于Qt、C++的毕业设计课设数学绘图工具（平面图、图表、立体图绘制-附下载链接）
介绍这是我的毕业设计，基于Qt Creator 4.11.1，c++语言。效果图如下点我下载项目源码（含打包软件）使用说明 1. 二维函数绘制开始界面：函数设置、输入界面：使用细节目前仅支持一元方程，如y=x^2,x=y+1 用户最开始只能选择输入x或y，其他符号均无法输入；输入x或y后
2024年02月03日
浏览(12)
K5 是平面图吗？
这个图就是著名的K5，有5个节点，每个节点都和其它节点全互联，构成一个5阶的完全图。 “传说”K5是最小的非平面图，也就是说，它是没法画在一个平面上，使得所有的边都能保持两两都不相交。以下一段DOT语言的代码代码可以让DOT生成一个K5。只是长相上不太好看。但
2024年01月17日
浏览(13)
推荐4款超简单的画平面图的软件
本篇文章将介绍 4 款目前热门的绘制平面图软件，包括即时设计、DRAW、Adobe PhotoShop 和 Adobe Illustrator。每一款软件的设计功能、易学性、性价比都不同，适用于不同的用户需求。其中，即时设计是一款新一代的协同设计工具，适用于团队项目，操作界面简单，易上手；DRAW 是一
2024年02月15日
浏览(13)
使用Pano2VR实现全景图切换和平面图效果
本文在文章《使用Pano2VR实现背景音乐、放大/缩小、旋转、缩略图和直线/立体/鱼眼模式等》基础上，增加全景图切换和平面图效果；效果如下图（为了可以上传缩小屏幕，属于PC端运行）： 1. 运行Pano2VR软件后，打开文章《使用Pano2VR实现背景音乐、放
2024年02月06日
浏览(13)
【图论】中国邮递员问题、平面图上最大割问题的多项式时间算法
中国邮递员问题（Chinese Postman Problem, CPP）是图论中的一个著名问题，它是在1960年由我国学者管梅谷首先提出并研究的。简单来说，就是问：一个邮递员从邮局出发，把一个城市的所有街道都至少走一遍，最后回到邮局，问怎样使他走的总路程最小？这个问题有许多现实的应
2024年02月12日
浏览(13)
VR全景图比平面图多了哪些优势，VR全景可以用在哪些领域
引言：在数字化时代，虚拟现实（VR）全景图成为了一种能在互联网上体验现实景观的新型展示形式，相对于传统图片，它在各行业都有显著的优势。一.VR全景图带来的优势 1.更真实的体验 VR全景图能够提供更加真实的视觉体验。与传统图片不同，VR全景图允许观众以720度的
2024年02月07日
浏览(10)
离散数学-集合论-关系的概念、表示和运算（7）
函数是x 到y 的映射，这种映射反就是一种关系。因为定义域x 是一个集合、值域y 也是一个集合所以函数就是一个x, y 有序对的集合。因此，我们可以通过二元关系来定义函数的概念，利用有序对的集合来表示函数。 1.1 有序对定义：由两个元素 x 和 y，按照一定的顺序组成的
2024年02月06日
浏览(12)
离散数学之矩阵关系运算
矩阵关系运算前提: (1)第一个矩阵的列数等于第二个矩阵的行数。 (2)两个矩阵的元素均是0或1。例如:A关系运算B得到C 原理：C11=(A11∧B11)∨(A12∧B21) C12=(A11∧B12)∨(A12∧B22)...... 就是把矩阵乘法中各个元素的乘法变成合取，原来乘法之后进行的相加改为合取后的析取。
2024年02月12日
浏览(14)
HNU-离散数学-工具箱系列3-关系矩阵法求传递闭包
用于解决这类问题：举例一、举例二、（求传递闭包）代码如下：
2024年02月11日
浏览(7)