【数值分析】用幂法计算矩阵的主特征值和对应的特征向量（附matlab代码）-Toy模板网

这篇具有很好参考价值的文章主要介绍了【数值分析】用幂法计算矩阵的主特征值和对应的特征向量（附matlab代码）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

题目

用幂法计算下列矩阵的按模最大特征值及对应的特征向量

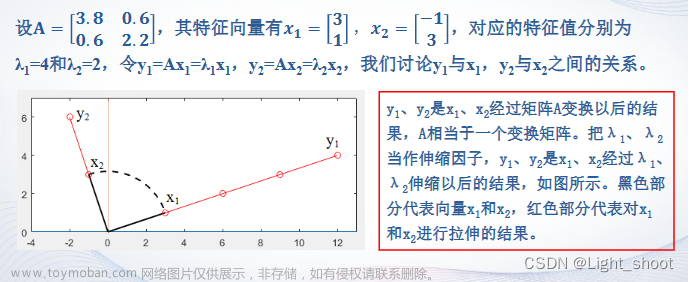
用幂法计算下列矩阵的主特征值及对应的特征向量,Matlab,# 数值分析,matlab,算法,幂法,特征值,特征向量

幂法

用幂法计算下列矩阵的主特征值及对应的特征向量,Matlab,# 数值分析,matlab,算法,幂法,特征值,特征向量

代码

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 简介：用幂法计算矩阵的主特征值和对应的特征向量
% 作者：不雨_亦潇潇
% 文件：mifa.m
% 日期：20221109
% 博客：https://blog.csdn.net/weixin_43470383
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
clc; clear all;
% A = [7 3 -2; 3 4 -1; -2 -1 3];
A = [3 -4 3; -4 6 3; 3 3 1];
u =[1; 1; 1];
err = 10^(-4);

% 第一次迭代
k = 1;
m0 = 1;
V =A*u;
m = max(V);
u = V/m;
disp('k=')
disp(k)
disp('V^T=')
disp(V')
disp('m=')
disp(m)
disp('u^T=')
disp(u')

while abs(m0-m)>err
    m0 = m;
    k = k+1;
    V =A*u;
    m = max(V); % V绝对值最大的分量
    u = V/m; % 规范化向量  
    disp('k=')
    disp(k)
    disp('V^T=')
    disp(V')
    disp('m=')
    disp(m)
    disp('u^T=')
    disp(u')
end

lambda = m0 % 最终得到的主特征值
vector = u % 最终得到的特征向量

题目1输出结果

k=
1
V^T=
8 6 0
m=
8
u^T=
1.0000 0.7500 0
k=
2
V^T=
9.2500 6.0000 -2.7500
m=
9.2500
u^T=
1.0000 0.6486 -0.2973
k=
3
V^T=
9.5405 5.8919 -3.5405
m=
9.5405
u^T=
1.0000 0.6176 -0.3711
k=
4
V^T=
9.5949 5.8414 -3.7309
m=
9.5949
u^T=
1.0000 0.6088 -0.3888
k=
5
V^T=
9.6041 5.8240 -3.7753
m=
9.6041
u^T=
1.0000 0.6064 -0.3931
k=
6
V^T=
9.6054 5.8187 -3.7857
m=
9.6054
u^T=
1.0000 0.6058 -0.3941
k=
7
V^T=
9.6056 5.8172 -3.7881
m=
9.6056
u^T=
1.0000 0.6056 -0.3944
k=
8
V^T=
9.6056 5.8168 -3.7887
m=
9.6056
u^T=
1.0000 0.6056 -0.3944
lambda =
9.6056
vector =
1.0000
0.6056
-0.3944

题目2输出结果

k=
1
V^T=
2 5 7
m=
7
u^T=
0.2857 0.7143 1.0000
k=
2
V^T=
1.0000 6.1429 4.0000
m=
6.1429
u^T=
0.1628 1.0000 0.6512
k=
3
V^T=
-1.5581 7.3023 4.1395
m=
7.3023
u^T=
-0.2134 1.0000 0.5669
k=
4
V^T=
-2.9395 8.5541 2.9268
m=
8.5541
u^T=
-0.3436 1.0000 0.3421
k=
5
V^T=
-4.0045 8.4010 2.3112
m=
8.4010
u^T=
-0.4767 1.0000 0.2751
k=
6
V^T=
-4.6047 8.7320 1.8451
m=
8.7320
u^T=
-0.5273 1.0000 0.2113
k=
7
V^T=
-4.9481 8.7432 1.6293
m=
8.7432
u^T=
-0.5659 1.0000 0.1864
k=
8
V^T=
-5.1387 8.8228 1.4886
m=
8.8228
u^T=
-0.5824 1.0000 0.1687
k=
9
V^T=
-5.2412 8.8359 1.4214
m=
8.8359
u^T=
-0.5932 1.0000 0.1609
k=
10
V^T=
-5.2969 8.8553 1.3814
m=
8.8553
u^T=
-0.5982 1.0000 0.1560
k=
11
V^T=
-5.3265 8.8606 1.3615
m=
8.8606
u^T=
-0.6011 1.0000 0.1537
k=
12
V^T=
-5.3425 8.8655 1.3502
m=
8.8655
u^T=
-0.6026 1.0000 0.1523
k=
13
V^T=
-5.3509 8.8673 1.3445
m=
8.8673
u^T=
-0.6034 1.0000 0.1516
k=
14
V^T=
-5.3555 8.8686 1.3413
m=
8.8686
u^T=
-0.6039 1.0000 0.1512
k=
15
V^T=
-5.3579 8.8692 1.3396
m=
8.8692
u^T=
-0.6041 1.0000 0.1510
k=
16
V^T=
-5.3592 8.8695 1.3387
m=
8.8695
u^T=
-0.6042 1.0000 0.1509
k=
17
V^T=
-5.3599 8.8697 1.3383
m=
8.8697
u^T=
-0.6043 1.0000 0.1509
k=
18
V^T=
-5.3602 8.8698 1.3380
m=
8.8698
u^T=
-0.6043 1.0000 0.1509
lambda =
8.8697
vector =
-0.6043
1.0000
0.1509文章来源地址https://www.toymoban.com/news/detail-790858.html