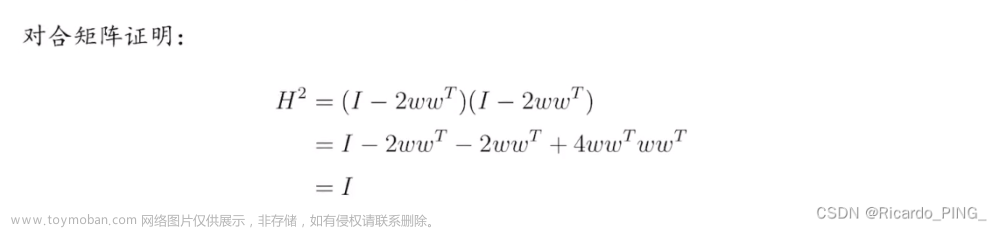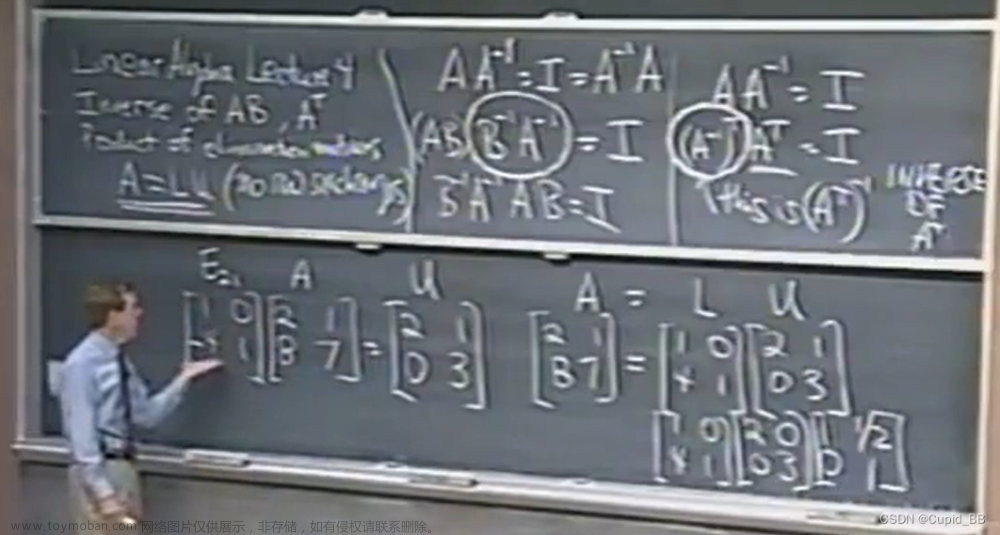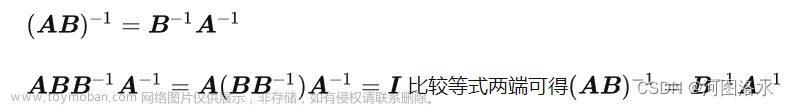本章重点内容：
满秩分解：存在性、方法
三角分解：Doolittle分解、两种求解方法、cholesky分解
QR分解：定义、Householder变换、Givens变换、Schmidt正交化方法求QR分解、上Hessenberg矩阵
奇异值分解
1 满秩分解
1.1满秩分解的基本概念和存在性
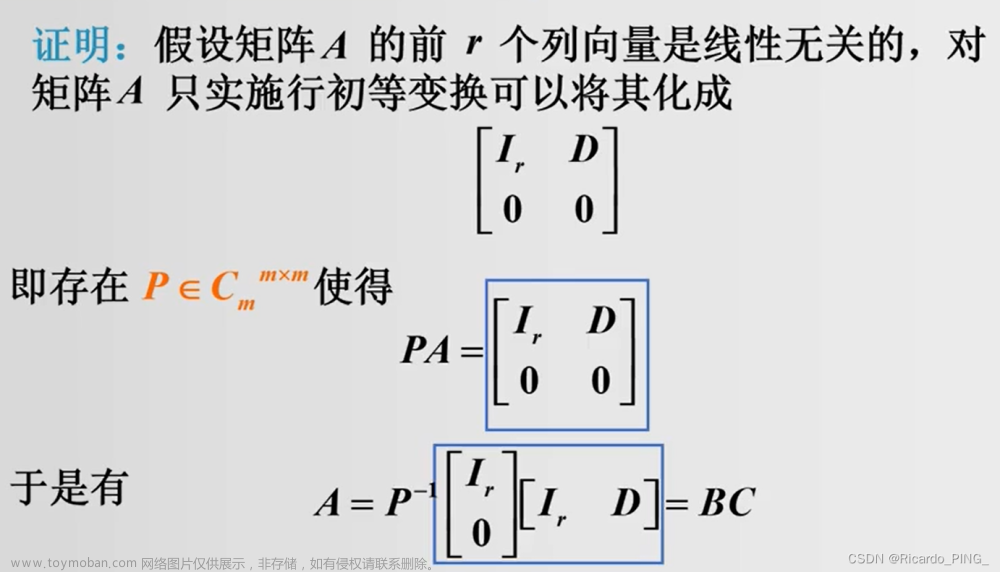
1.2 满秩分解的方法
下面看个例子，对矩阵进行满秩分解
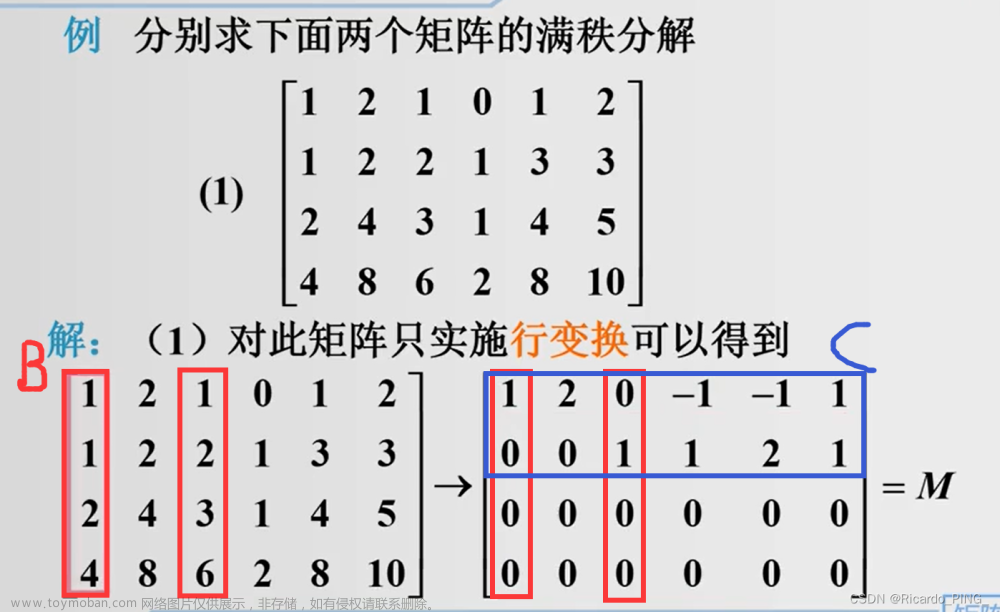
1.3 其他定理
2 矩阵三角分解（LU分解）
矩阵的三角分解是最基本的一种矩阵分解,它是将一个矩阵分解成一个下三角矩阵L和一个上三角矩阵U的乘积. 矩阵的三角分解是最基本的一种矩阵分解，它是将一个矩阵分解成一个下三角矩阵L和一个上三角矩阵U的乘积.
2.1 上三角矩阵和下三角矩阵
- 三角分解是方阵A的分解
- 如果主对角线上的元素都是1，存在单位下三角矩阵和单位上三角矩阵。
2.2 LU分解、LDU分解、Doolittle分解、Crout分解
从Doolittle分解可以求出LDU分解和Crout分解
2.2.1 LU分解不唯一性
2.2.2 LDU分解
2.2.3 Doolittle分解及两种求解方法
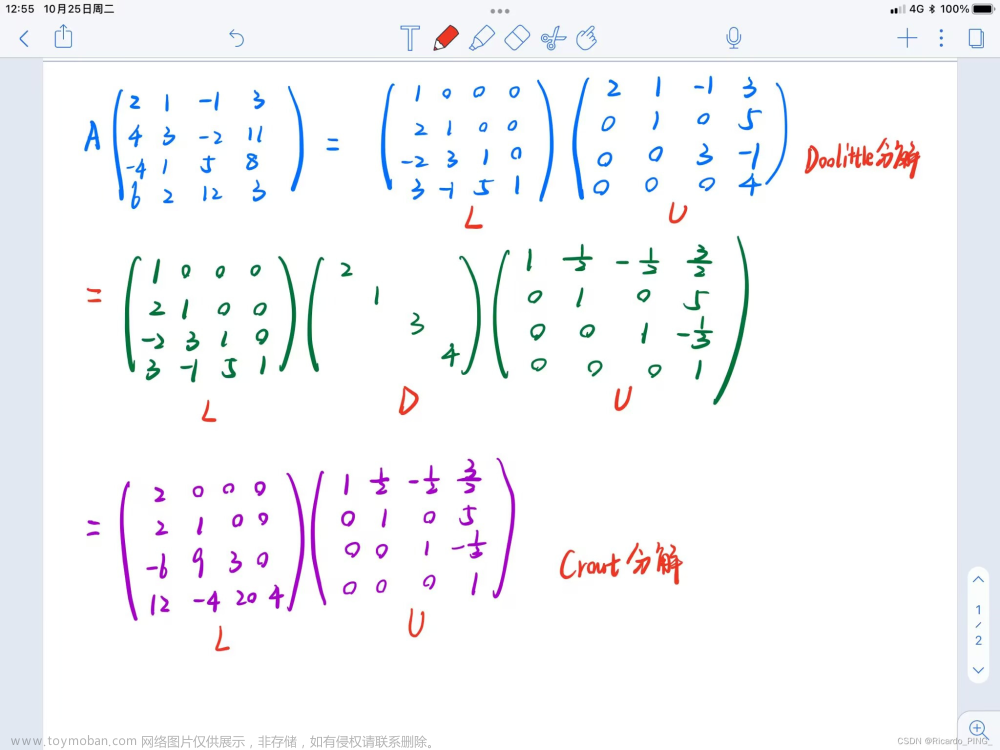
可以只研究Doolittle分解
求Doolittle分解的两种方法
2.2.4 选列主元的Doolittle分解
下面看一道例题
2.3 Cholesky分解
2.3.1 Cholesky分解方法
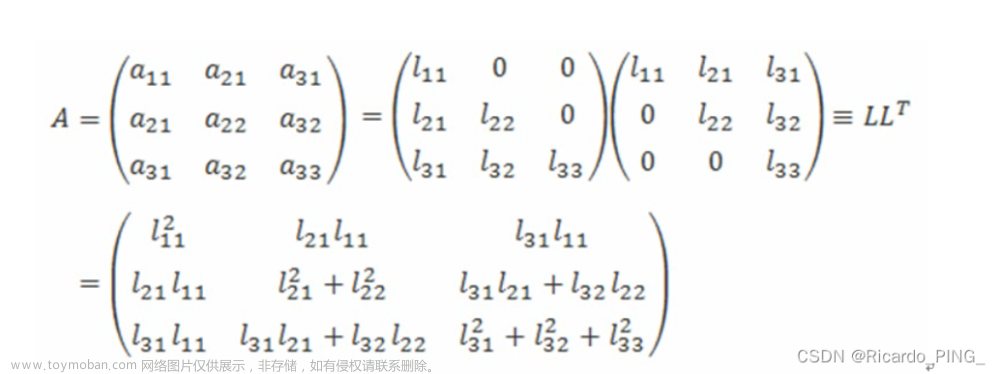
2.3.2 改进的Cholesky分解方法
3 QR分解
3.1 QR分解的定义
条件数变化问题
解决办法
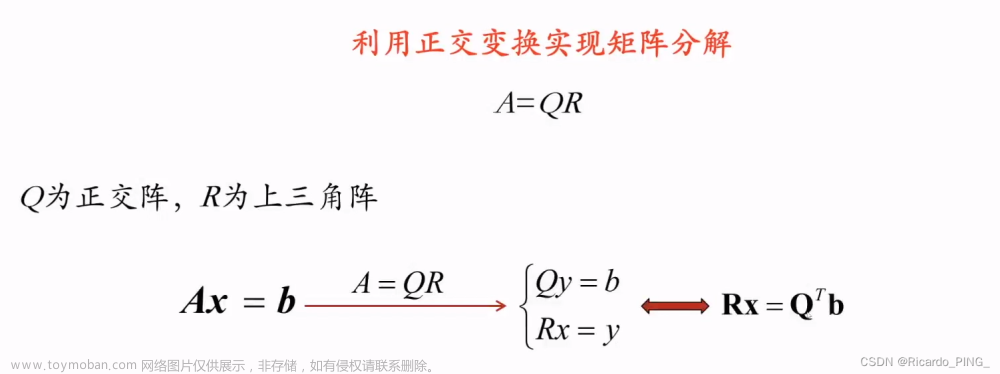
QR分解
QR（正交三角）分解法是求一般矩阵全部特征值的最有效并广泛应用的方法，一般矩阵先经过正交相似变化成为Hessenberg矩阵，然后再应用QR方法求特征值和特征向量。它是将矩阵分解成一个正规正交矩阵Q与上三角形矩阵R，所以称为QR分解法，与此正规正交矩阵的通用符号Q有关。
如果实（复）非奇异矩阵A能够化成正交（酉）矩阵Q与实（复）非奇异上三角矩阵R的乘积，即A=QR，则称其为A的QR分解。
3.2 Householder变换
3.2.1 几何观点
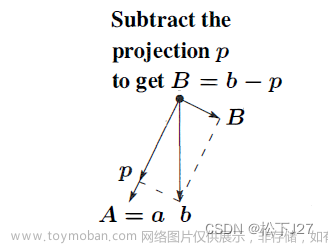
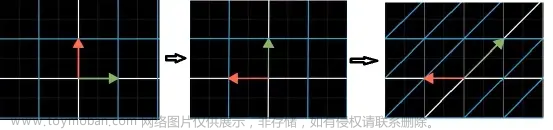
矩阵消元的几何观点
镜面反射
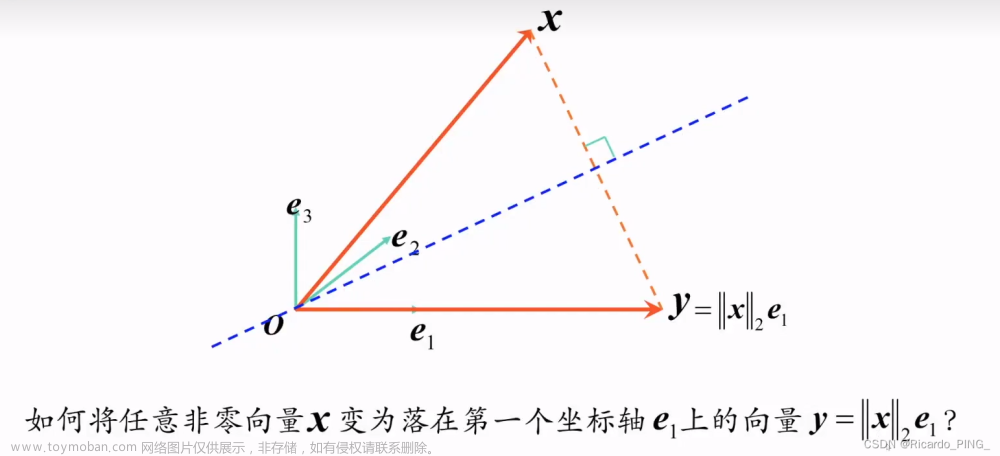
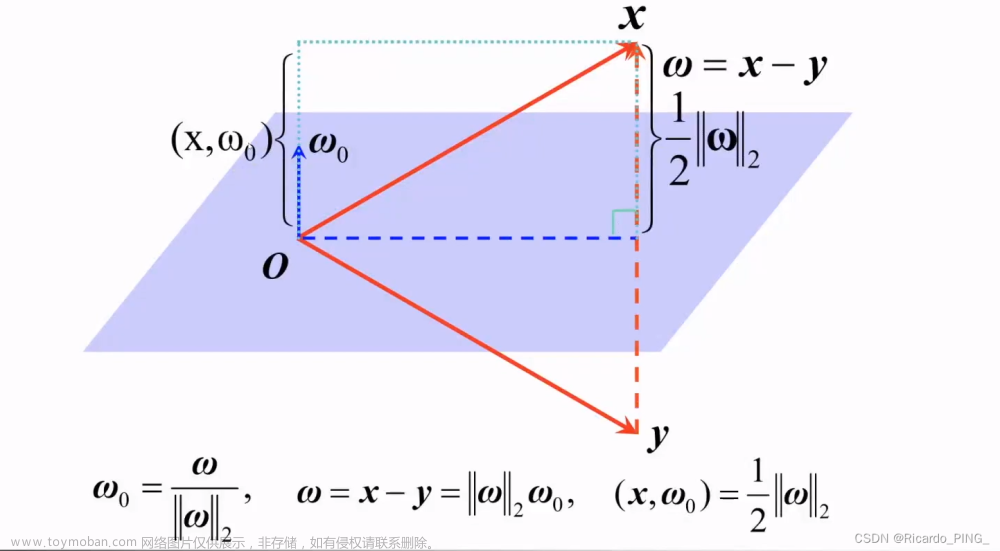
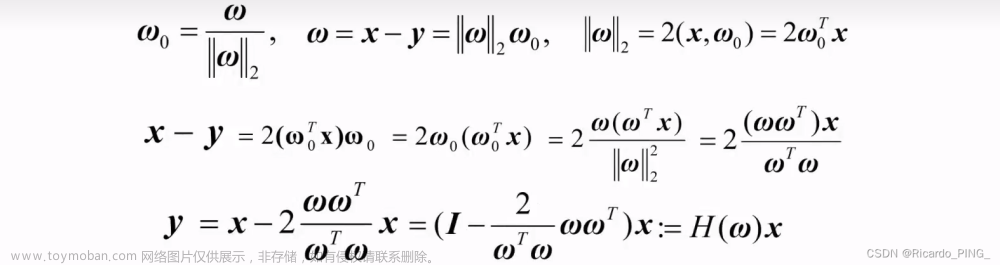
3.2.2 Householder矩阵
w是单位列向量是指模长为1
3.2.3 Householder矩阵的性质
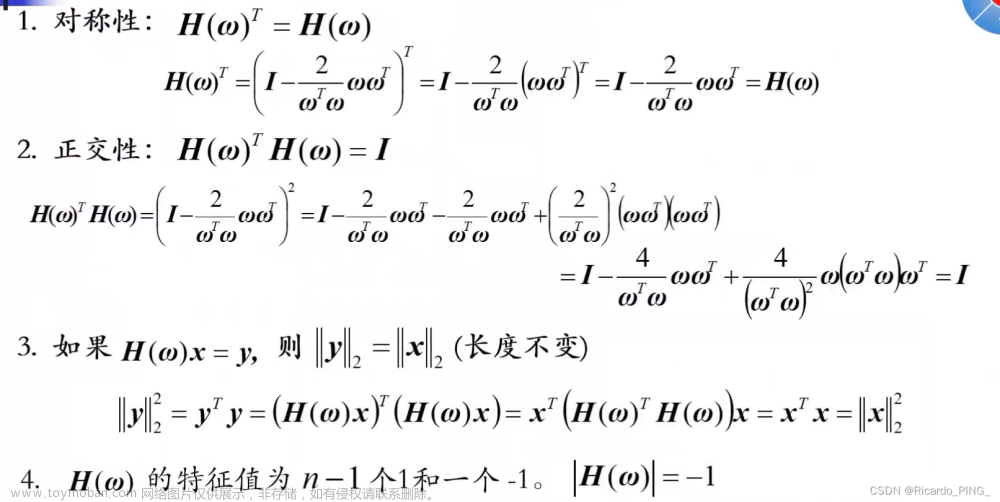
三个定理
3.2.4 Househloder变换的例题
3.2.5 用HouseHolder变换进行QR分解
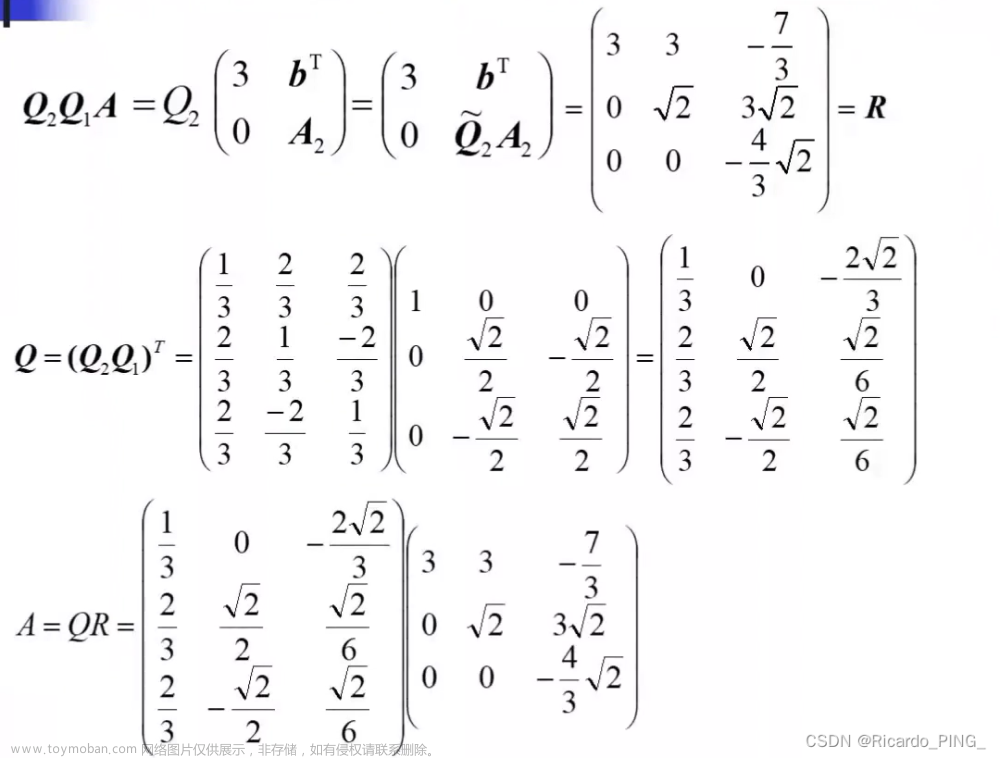
有时候会有些规定，故进行QR矩阵的转换
3.3 Givens变换
3.3.1 Givens旋转定义
初等旋转变换或者说是吉文斯(Givens)变换是一种正交变换，经过多次吉文斯(Givens)变换可以把矩阵转换成上三角形式，是一种常用的QR分解方式。
3.3.2 性质
3.3.3 应用
3.3.4 Givens变换的例题
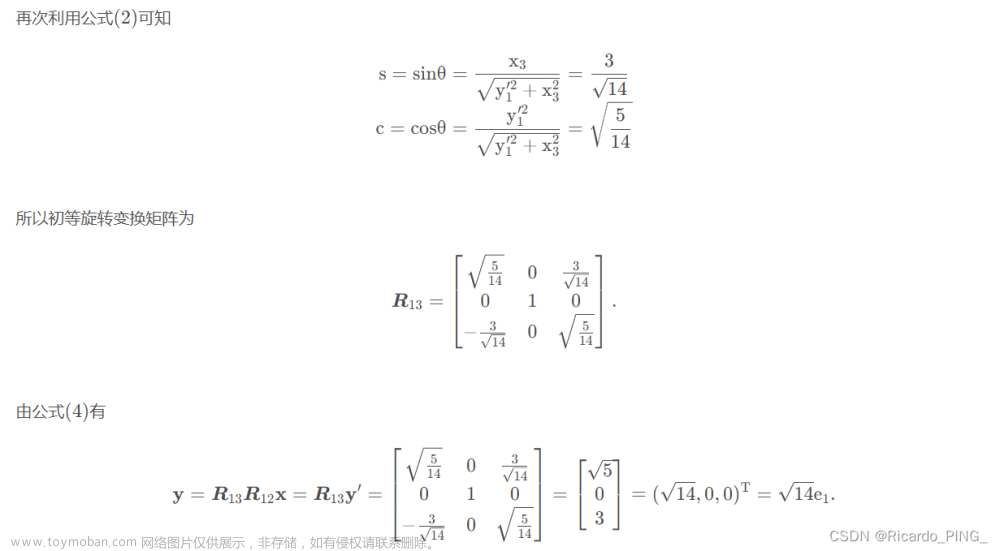
3.3.5 用Givens变换进行QR分解
3.4 施密特进行QR分解
3.5 上Hessenberg矩阵
3.5.1 用Householder变换为Hessenberg矩阵
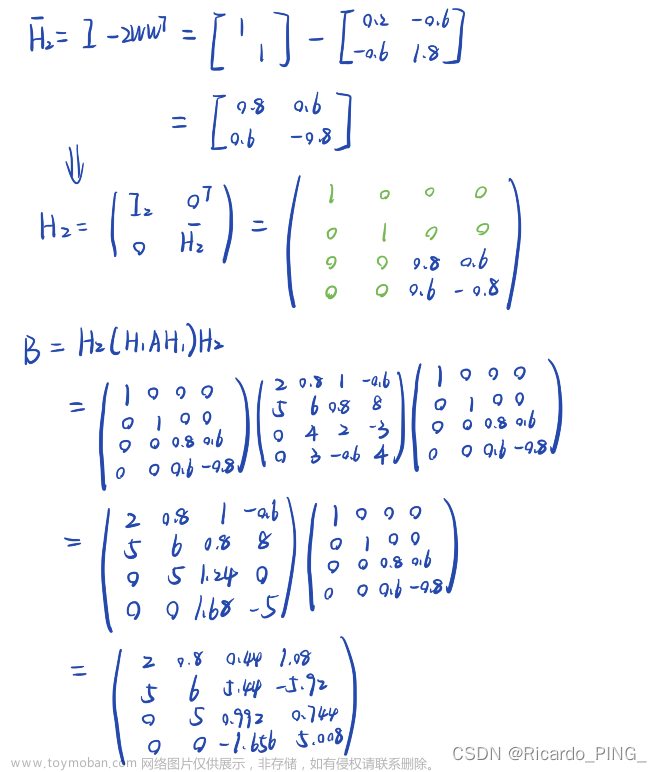
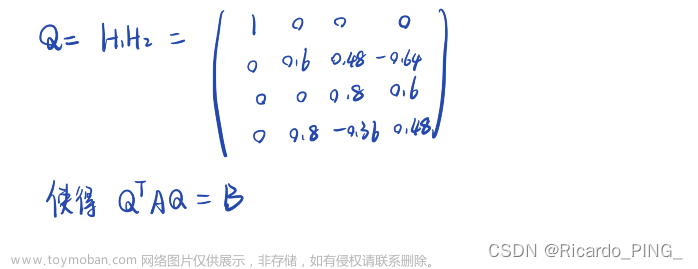
3.5.2 用Givens变换为Hessenberg矩阵
4 矩阵的奇异值分解
4.1 奇异值分解定理
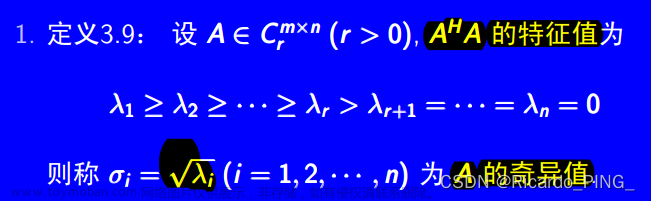
4.2 求奇异值分解
约化的奇异值分解
满奇异值分解
4.3 奇异值分解讨论矩阵的性质
文章来源：https://www.toymoban.com/news/detail-791200.html
文章来源地址https://www.toymoban.com/news/detail-791200.html
到了这里，关于矩阵分析与计算学习记录-矩阵分解的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！
