创作背景
看到一道题目有感而发想写一篇题解,涉及的是一种逆向思维
桌面窗体重叠 - 洛谷https://www.luogu.com.cn/problem/U399827题目来源于《信息学奥赛课课通》
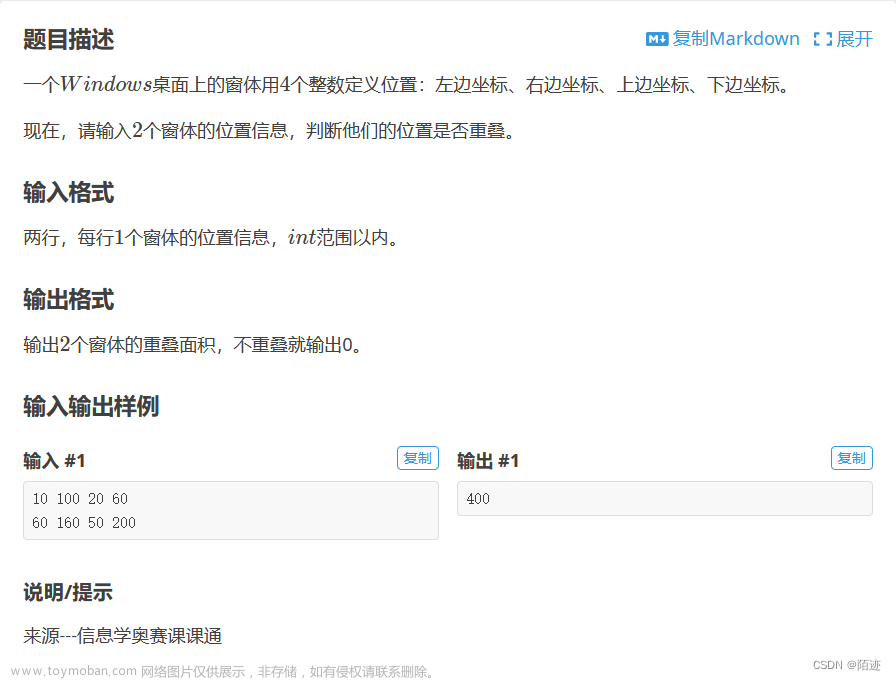
大致就是给一个长方形的左上顶点坐标(x1,y1)和右下顶点坐标(x2,y2),一个长方形的左上顶点坐标(x3,y3),右下顶点(x4,y4),然后判断这两个长方形是否重合。
思路呈现
1.一开始想的是从判断一个点是否在一个长方体内->判断一个长方形是否有点在另一个长方形中
代码如图:(显而易见的蠢)

2.逆向思维的利用
判断两个长方形是否不重叠 判断两条线段是否不相交->判断两个长方形是否相交
比如说在x轴上,我判断(x1,0)和(x2,0)的线段和(x3,0)和(x4,0)的线段是否相交的话,要考虑四种情况(因为不知道x1和x3的大小、x2和x4的大小)
if(x3<x1<x4||x3<x2<x4||x1<x3<x2||x1<x4<x2)
但是如果考虑不相交的话,最小值大于最大值,最大值小于最小值就不想交了
if(x3>x2||x4<x1)
显然简单了很多。
然后在y轴上考虑不相交
if(y3>y2||y4<y1)
只要在x、y轴上有一个判断不相交,这这两个长方形也不会相交,所以逻辑用或
合起来判断是否相交,true为相交。
if(!(x3>x2||x4<x1||y3>y2||y4<y1))
再利用德·摩根定律
非(P 且 Q) = (非 P) 或 (非 Q)
非(P 或 Q) = (非 P) 且 (非 Q)
可以把条件更改为如下的条件:
if(x3<=x2&&x4>=x1&&y3<=y2&&y4>=y1)
完整代码:
#include<iostream>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
int main() {
int x1,x2,x3,x4,y1,y2,y3,y4;
cin>>x1>>x2>>y1>>y2>>x3>>x4>>y3>>y4;
if(x3<=x2&&x4>=x1&&y3<=y2&&y4>=y1){
int left=max(x1,x3);
int right=min(x2,x4);
int top=max(y1,y3);
int bottom=min(y2,y4);
// cout<<left<<endl;
// cout<<right<<endl;
// cout<<top<<endl;
// cout<<bottom<<endl;
int s=(right - left) * (bottom - top);
cout<<s;
}else{
cout<<0;
}
return 0;
}
扩展
如何用编程N个人中解决至少两个人的生日在同一天的问题
1.至少两个人,那要考虑2个人,3个人,......n个人生日在同一天的情况。就比较复杂。
2.使用了逆向思维的话
过来想,N个人生日全不相同的概率:365/365*(364/365)*(363/365)*...*[(366-n)/365]…………[即后N-1个人与前面的人都不一样]
=364!/[(365-n)!·365^(N-1)]文章来源:https://www.toymoban.com/news/detail-814668.html
(第一个人的生日可以在任何一天,第二个人的生日是除了第一个人生日那天外的任何一天.......)
所以至少有两人是同一天生日的概率为1-364!/[(365-n)!·365^(N-1)].文章来源地址https://www.toymoban.com/news/detail-814668.html
到了这里,关于矩阵重叠问题判断的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!




