机器视觉【3】非线性求解相机几何参数

线性求解相机几何参数的缺点

上一章节介绍学习了（DLT）线性求解相机几何参数，了解到线性求解法当中比较明显的缺点：

• 没有考虑到镜头畸变的影响
• 不能引入更多的约束条件融入到DLT算法当中优化
• 最关键的是，代数距离并不是计算相机矩阵的最佳距离函数

基于以上问题点，提出非线性求解方法。

• 将包括镜头畸变参数、内外参矩阵等所有信息都当做待求解
• 定义一个比代数距离更好的距离函数
• 通过迭代的非线性最优化算法，最优化上述距离函数，从而得到待求解

在《计算机视觉中的多视角几何》的第7.2节中，用一个插图来说明了线性求解出来的代数距离的几何意义。可以看见，代数距离实际上优化的是已知的3D点X和2D点Xi的反投影点Xi'之间的距离。这并不是一个最优的距离函数。

下面我们来看看几何距离，这里假设3D点的位置是准确的（比如我们有一个制作得非常精确的标定板），如下图所示。那么几何距离就是3D点Xi通过投影矩阵投影的2D点xi'和实际成像的2D点xi之间的距离（下图中的红线段）

用公式表达式如下所示，整个优化过程就变成了最小化这个距离的过程，如(2)式

结合之前在 相机的成像(畸变)模型 中的数学模型，式子(2)又可以演变为如下的式子(3)

为了执行这个最优化的过程，需要给相机矩阵及畸变参数初始值。其中P的初始值可以用第一节所讲述的DLT算法得到。而畸变参数的初值可以先设置为0。 

张正友标定法的实现和完整的过程

在相机几何标定的各种算法中，最出名的无疑是张正友博士发明的“张氏标定法”，这个算法在整个业界得到了广泛的应用，它最大的特点就是灵活、鲁棒、低成本。整个标定过程只需要用相机在不同的方向拍摄平面标定板（最少两次），而它实际上的核心思想就是我上面描述的非线性优化求解方法。

在Matlab和OpenCV中都有张氏标定法的实现，具体使用时先准备好一个足够平整的棋盘格标定板，然后通过不同的方向对标定板进行拍摄，然后进行计算。不需要提前知道相机和标定板之间的具体位姿关系，每次拍摄时的相机和标定板的位姿变换也是独立的，整个使用过程非常友好。

在Matlab中，把上面这些图像输入算法，算法会自动检测出棋盘格角点，并利用前面说的方法优化出各项参数，如果某幅图的平均投影误差超出了用户设置的阈值，还可以方便的过滤掉这幅图来重新进行优化计算。甚至还可以可视化每次拍摄时相机和标定板的位姿，非常方便。

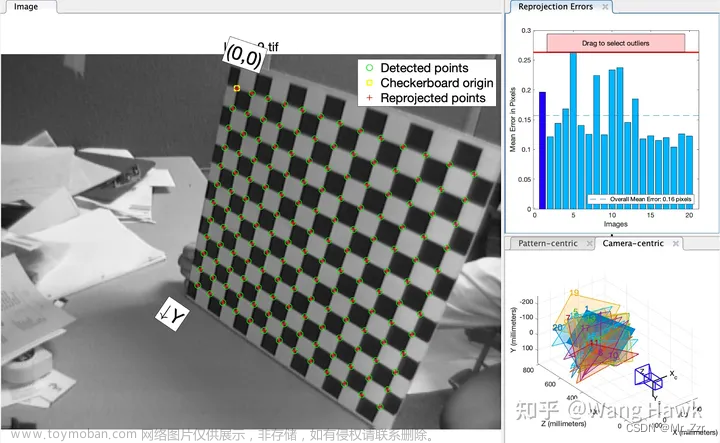
下面简单介绍张正友标定法的关键知识要点。

要点1：引入新的约束条件，从而可以采用平面标定板替代立体标定板

之前讲过标定板需要是立体的，否则无法唯一确定相机矩阵。 然而，立体的标定板是较难去制作的，张氏标定法追求的是低成本的标定方式，因此采用了多次拍摄平面标定板的方式来执行标定。而正因为是多次拍摄，所以每次拍摄时相机矩阵都是变化的，之前讲解的约束条件不再适用：

因此，张氏标定法重新寻求了新的约束条件，用于对内参矩阵进行约束，进而进行求解。作者观察到平面板上的点和对应的像点之间可以用一个单应矩阵H关联在一起，而且只要平面板上的角点足够多（单应矩阵有8个自由度，一对点提供2个约束，所以理论上超过4个即可），就可以求出这个单应矩阵，求解方法类似于上一节所介绍的DLT方法；或者之前学习过的 几何变换模型 中的透视模型，利用最小二乘法求解。

接下重点：作者将单应矩阵表达为H，并观察到内参矩阵K和单应矩阵之间存在着一对约束关系。

怎么理解上面的两个等式？回想 机器视觉【1】相机的成像(畸变)模型 整合：世界坐标系→像素坐标系的知识点

这里的λ只是1/s的另一种表示，只是换了一种写法

这里有人会不理解，r1=和r2=是怎么来的？其实自己可以推导一下，把A设成[3X3]的矩阵，乘进去，应该能够看到，组成了[Ar1 Ar2 Ar3]，它们互相还是独立的。至于为什么A到A逆，这个是线性代数最基本的转换，左右同时左乘A逆，就变过来了。

这里的A其实就是内参矩阵K，上面两个式子其实不难证明 (以下 A' 为 矩阵A的逆 即上图示的A-1)

由前置知识：A'H = A' · λ · A · [r1 r2 t​] = [r1 r2 t​]，λ是常数可暂时忽略

根据线性代数基本规律：(AB)T = BT · AT 即 矩阵A和B相乘之后的转置等于B的转置乘A的转置

那么：(h1)T​ * (A)−T * (A)−1 * h2​ = r1T * ​r2​ = 0    

第一个公式证得r1和r2是正交的关系。

对第二个式子左右两边进行上述变换，得 r1T * ​r1 = r2T * ​r2，由此可知 r1和r2是单位正交。

最后，我们把上述的两个式子中间 (K)-T*(K)-1的部分记作B，其余h部分利用线性基础变换写出另外一部分。即如下表示

这样，我们又可以用SVD奇异值分解的方式，求得b，进而求得K的各个元素。当求得了K之后，就很容易得到这一次拍摄时的外参信息（旋转R和平移t）了。上面讲的方法用于初始化内参矩阵K和每次拍摄的外参R和t，我们假设一共进行n次拍摄，每次拍摄可以获得m个成像点，那么就可以利用非线性最优化方法，来最优化待解参数了。具体表达式如下： 

要点2：在多次拍摄时，需要改变标定板的方向

在张博士的论文中详述了如果两次拍摄时的标定板是平行的，那么实际上并没有提供额外的信息，也因此无法求解出需要的参数。

要点3：最少需要拍摄几幅图？

前面讲到，每一幅拍摄的标定板图像提供了2个对内参矩阵K的约束，而我们内参矩阵K一共有5个未知参数，所以理论上至少需要拍摄3幅图像，才能求得K：

如果我们认为s=0，即传感器像素是规整方形的，那么内参矩阵就只有4个未知参数了，这样就只需要拍摄两幅图像就能进行标定了。

前面讲过，这样的约束关系是为了求得比较好初始化内参矩阵K的。如果你能够事先知道K中元素的大概值，比如你认为s=0， 主点位于图像的中心， 而焦距又是已知的，那么理论上你只需要拍摄一幅平面的标定板一次，就可以通过非线性最小二乘法标定出相机的内外参数。

Reference：

张正友相机标定全解析_定焦相机张正友标定法怎么用-CSDN博客

相机标定（具体过程详解）张正友、单应矩阵、B、R、T_已知内参数下标定r、t-CSDN博客

总结

前文和本文中讲解了相机标定的两大类方法：线性求解方法，以及非线性求解方法。

不管是哪种方法，我都提到了数据归一化的重要性，因为在求解过程中的矩阵元素如果不经过归一化，值差异较大，很容易放大数值误差，需要特别注意这点。经过相机的标定，我们就可以获得了包括畸变参数在内的相机内参，以及每次拍摄时的外参。

博主我的自述：

说实话，之前是知道这一块比较复杂，但没想过是这么复杂。现实接触的情况都是用现成的库或者软件工具一键处理，这次花力气去理解算是 "拨开云雾见天日，守得云开见月明"，新的一年祝大家工作顺利，万事如意，大家加油！文章来源地址https://www.toymoban.com/news/detail-833278.html

到了这里，关于机器视觉【3】非线性求解相机几何参数的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！