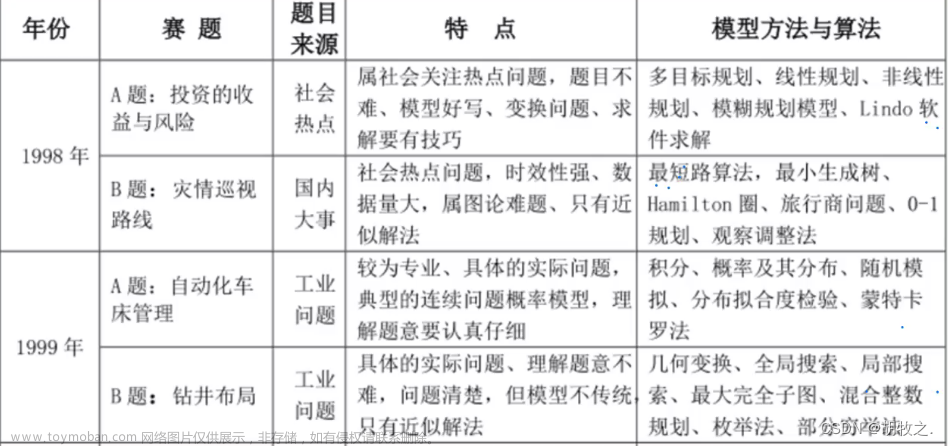
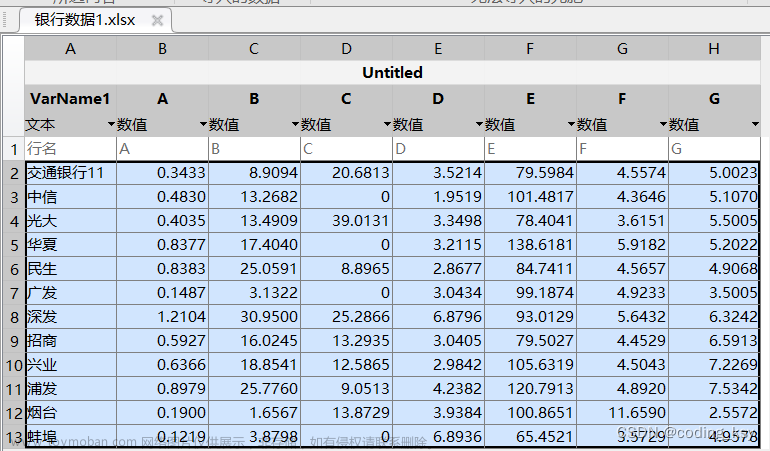
一、模糊综合评价分析简介
提到模糊综合评价分析,就先得知道模糊数学。1965年美国控制论学家L.A.Zadeh发表的论文“Fuzzy sets”标志着模糊数学的诞生。
模糊数学又称Fuzzy数学,是研究和处理模糊性现象的一种数学理论和方法。模糊性数学发展的主流是在它的应用方面。由于模糊性概念已经找到了模糊集的描述方式,人们运用概念进行判断、评价、推理、决策和控制的过程也可以用模糊性数学的方法来描述。例如模糊聚类分析、模糊模式识别、模糊综合评判、模糊决策与模糊预测、模糊控制、模糊信息处理等。这些方法构成了一种模糊性系统理论,构成了一种思辨数学的雏形,它已经在医学、气象、心理、经济管理、石油、地质、环境、生物、农业、林业、化工、语言、控制、遥感、教育、体育等方面取得具体的研究成果。
这里要对模糊有个概念。举数学归纳法和秃子悖论为例。我们知道数学归纳法的证明步骤,但考虑这么一种情况:小魏满头秀发,减少一根头发,不是秃子,假设减少k根不是秃子,那么减少k+1根也不是秃子,但真的是这样吗?
对这种情况的解释,文学给出:这是压死骆驼的最后一根稻草;哲学给出:量变引起质变;数学给出:引入模糊概念。
来看数学中研究的量的划分
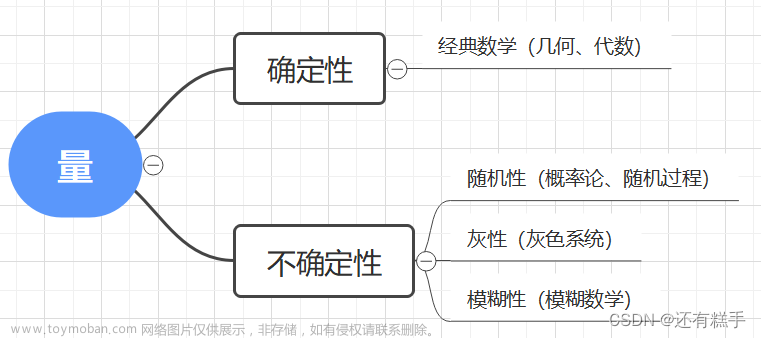
而生活中处处存在模糊性(和确定性相对)
- 确定性概念:性别、天气、年龄、身高、体重...
- 模糊性概念:帅、高、白、年轻...
像性别可以确定知道,年龄也是一个准确的数。而帅,什么才叫帅,长成什么样才叫帅?这是模糊的。
二、适用赛题
综合评价类,和前面的综合评价类模型差不多。
三、模型流程

四、流程分析
1.确定三集
三集分别是:因素集、评语集、权重集。但在确定它们之前先来了解模糊集合和隶属函数的概念。
模糊集合(Fuzzy set)和隶属函数
- 模糊集合:用来描述模糊性概念的集合(帅、高、白、年轻)
- 与经典集合相比,模糊集合承认亦此亦彼(即a ∈ A和a ∉ A可以同时发生)
- 数学中对于模糊集合的刻画:隶属函数(membership function)
举个例子。A = “年轻”(年轻是一个模糊概念),U = (0, 150)表示年龄的集合,有

对于U中每一个元素,均对应于A中的一个隶属度,隶属度介于[0, 1],越大表示越属于这种集合。
注意
- UA(x)不唯一
- 若对于一个模糊集合A我们给定了一个隶属函数UA,则我们可以将A和UA视为等同(方便符号表示,即A(x) = UA(x))
模糊集合的分类
一般的,可以将模糊集合分为三类:
- 偏小型:年轻、小、冷
- 中间型:中年、中、暖
- 偏大型:年老、大、热
可以想象,隶属函数的图像会和模糊集合的类型有很大关系

模糊评价问题是要把论域(集合论知识,不知道没关系)中的对象对应评语集中一个指定的评语后者将方案作为评语集并选择一个最优的方案。(两个角度)
在模糊综合评价中,引入了三个集合:
- 因素集(评价指标集):U = {u1, u2, ..., un}
- 评语集(评价的结果):V = {v1, v2, ..., vm}
- 权重集(指标的权重):A = {a1, a2, ..., an}
例如:评价一个学生的表现
U = {专业排名, 课外实践, 志愿服务, 竞赛成绩}
V = {优, 良, 差}
A = {0.5, 0.1, 0.1, 0.3}
在指标个数较少的评价中,运用一级模糊综合评判,而在问题较为复杂,指标较多时,运用多层次模糊综合评判(后面讲解),以提高精度。
对于因素集,一级模糊评价中,n往往较小(n ≤ 5)且指标间相关性不强。对于评语集,评语的个数与指标的个数无关。对于权重集,如何确定权重,用通用的方法即可,无数据:层次分析法,有数据:熵权法。
2.确定模糊综合判断矩阵
对指标ui来说,对各个评语的隶属度记为Ri向量,Ri = [ri1, ri2, ..., rim],分别是指标ui对评语1的隶属度,指标ui对评语2的隶属度,...,指标ui对评语m的隶属度。
将R1、R2、...、Rn组成一个n×m阶的矩阵,这就是各指标的模糊综合判断矩阵,第一列就是各个指标对于评语1的隶属度。
所以现在只需要得到隶属度就行了。
确定隶属度有三个方法
(1)模糊统计法(数模比赛中很少用,要设计发放问卷,可能来不及,但实际做研究用的较多)
原理:找多个人去对同一个模糊概念进行描述,用隶属频率去定义隶属度。
例子:定义“年轻人”的隶属函数
- 定义人的年龄为论域U,调查n个人
- 让这n个人仔细考虑好“年轻人”的含义后,给出他们认为的最合适的年龄区间
- 对于任意一个确定的年龄,例如25岁,若这n个人中有m个人的年龄区间包含有25,则称m/n为25岁对于“年轻人”的隶属频率
- 依此类堆,我们可以找出所有年龄对子“年轻人的隶属频率
- 若n很大时,隶属频率会趋于稳定,此时我们可将其视为隶属度,进而得到隶属函数
(2)借助已有的客观尺度(需要有合适的指标,并能收集到数据)
如下图例子
| 论域 | 模糊集 | 隶属度 |
| 设备 | 设备完好 | 设备完好率 |
| 产品 | 质量稳定 | 正品率 |
| 家庭 | 小康家庭 | 恩格尔系数 |
注意:这里找的指标必须介于0和1之间(隶属度范围)。(如果不是,进行归一化处理)
(3)指派法(根据问题的性质直接套用某些分布作为隶属函数,主观性较强)

找到适合的方法,得到隶属函数进而得到隶属度,从而得出模糊综合判断矩阵。
3.综合评判
当我们有了模糊综合判断矩阵R和权重集A,就可得到综合评判结果B = A * R。
B是一个向量,B = [b1, b2, ..., bm],分布是要评价对象对评语1的隶属度,要评价对象对评语2的隶属度,...,要评价对象对评语m的隶属度。
若max{b1, b2, ..., bm} = bk,则要评价的对象要划分到评语k这一类。
4.多级模糊综合评判
例子如下

评价指标可以划分出层级,那么就需要使用多级模糊综合评判了。上图就是三级模糊综合评判。文章来源:https://www.toymoban.com/news/detail-841815.html
不过这个其实就是多个一级模糊综合评判。得到每一级的指标对于评语的隶属度,求出上一级指标对于评语的隶属度,从后面往前面求,从n级往1级求,最后得出结果。文章来源地址https://www.toymoban.com/news/detail-841815.html
到了这里,关于数学建模【模糊综合评价分析】的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!