9.动态规划——4.最长公共子序列（动态规划类的算法题该如何解决？）

这篇具有很好参考价值的文章主要介绍了9.动态规划——4.最长公共子序列（动态规划类的算法题该如何解决？）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

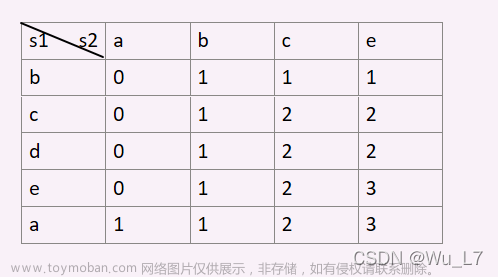
例题——最长公共子序列(一)

9.动态规划——4.最长公共子序列（动态规划类的算法题该如何解决？）,Practice,动态规划,算法

分析

设最长公共子序列 $d p [i] [j]$ 是 $S_1$ 的前 $i$ 个元素，是 $S_2$ 的前 $j$ 个元素，那么有：

若 $S_1[i-1]==S_2[i-1]$ ，那么 $d p [i] [j] = d p [i - 1] [j - 1] + 1$
若 $S_1[i-1] !=S_2[i-1]$ ，那么 $d p [i] [j] = ma x (d p [i] [j - 1], d p [i - 1] [j])$

代码

#include <cstdio>
#include <string>
#include <map>
#include <algorithm>
#include <vector>
#include <queue>
#include <stack>
#include <climits>
//#include <bits/stdc++.h>
using namespace std ;
#define N 1001
int dp[N][N];

int main(){
    int m,n;
    char s1[N];
    char s2[N];
    scanf("%d%d",&n,&m);
    scanf("%s%s",s1,s2);
    for (int i = 0; i <= n; ++i) {
        for (int j = 0; j <= m; ++j) {
            if (i==0||j==0){
                dp[i][j]=0;
                continue;
            }
            if (s1[i-1]==s2[j-1]){
                dp[i][j]=dp[i-1][j-1]+1;
            } else{
                dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
            }
        }
    }
    printf("%d\n", dp[n][m]);

    return 0;
}

动态规划类的算法题该如何解决？

动态规划（Dynamic Programming，简称 DP）是一种在数学、计算机科学和经济学中使用的，通过把原问题分解为相对简单的子问题的方式来求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

解决动态规划类的算法题，一般遵循以下步骤：

理解问题：首先，需要完全理解问题的要求。这包括问题的输入、输出以及约束条件。对于动态规划问题，通常要找到问题的“状态”和“状态转移方程”。
定义状态：状态是描述问题在某个特定时刻的情况的变量或变量组。在动态规划中，我们需要找到一组状态，使得原问题的解可以由这些状态导出。每个状态都应该对应原问题的一个子问题。
寻找状态转移方程：状态转移方程描述了如何从较简单的子问题的解（即较小状态的值）推导出较复杂子问题的解（即较大状态的值）。这通常涉及对问题的数学建模。
初始化边界条件：对于动态规划问题，通常需要为最小的子问题（即边界状态）设定初始值。这些初始值通常是直接给出的，或者是通过简单计算得到的。
自底向上求解：根据状态转移方程和边界条件，从最小的子问题开始，逐步求解更大的子问题，直到求得原问题的解。这通常涉及使用循环或递归来遍历状态空间。
返回结果：当所有状态都被计算完毕后，原问题的解就是特定状态的值。这个状态通常是状态空间中的最大或最小状态，具体取决于问题的定义。

下面是一个简单的例子，说明如何应用这些步骤来解决动态规划问题：

例子：0-1背包问题

给定一组物品，每种物品都有自己的重量和价值。在限定的总重量内，我们如何选择，才能使得物品的总价值最大。

理解问题：有n个物品和一个容量为W的背包，每种物品i有重量weight[i]和价值value[i]。问题是如何选择物品放入背包，使得背包内物品的总价值最大。
定义状态：定义dp[i][j]为前i个物品中选取若干个放入容量为j的背包中所能获得的最大价值。
寻找状态转移方程：对于第i个物品，我们有两种选择：放入背包或不放入背包。如果放入背包，则背包的剩余容量为j-weight[i]，此时的价值为dp[i-1][j-weight[i]] + value[i]；如果不放入背包，则价值为dp[i-1][j]。因此，状态转移方程为：dp[i][j] = max(dp[i-1][j], dp[i-1][j-weight[i]] + value[i])。
初始化边界条件：当没有物品可选（即i=0）时，dp[0][j] = 0（因为没有任何物品可以放入背包）；当背包容量为0时，无论有多少物品可选，dp[i][0] = 0（因为无法放入任何物品）。
自底向上求解：使用两层循环遍历所有状态。外层循环遍历物品（从1到n），内层循环遍历背包容量（从0到W）。在每个状态下，根据状态转移方程计算dp[i][j]的值。
返回结果：当所有状态都被计算完毕后，原问题的解就是dp[n][W]，即前n个物品中选取若干个放入容量为W的背包中所能获得的最大价值。