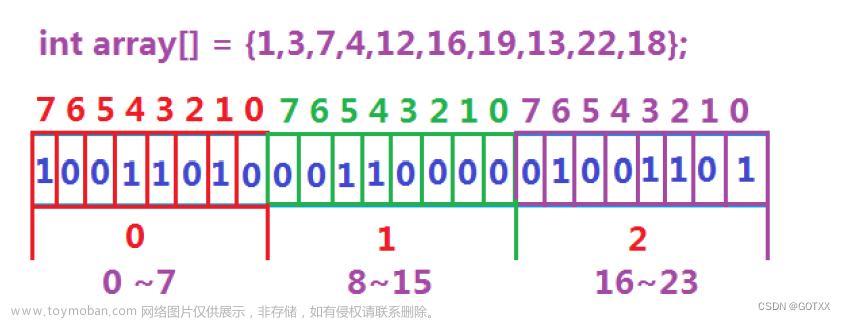
一、位图实现
1.1位图的原理
#pragma once
#include<iostream>
#include<vector>
#include<assert.h>
using namespace std;
namespace gazbitset
{
template<size_t N>
class bitset
{
public:
bitset()
{
_bits.resize(N/32+1,0);
}
//将x映射的位置标记成1
void set(size_t x)
{
assert(x <= N);
size_t i = x / 32;
size_t j = x % 32;
_bits[i] |= (1 << j);
}
// 把x映射的位标记成0
void reset(size_t x)
{
assert(x <= N);
size_t i = x / 32;
size_t j = x % 32;
_bits[i] &= ~(1 << j);
}
//查找一个值是否在位图中,在就返回1,不在返回0
bool test(size_t x)
{
assert(x <= N);
size_t i = x / 32;
size_t j = x % 32;
return _bits[i] & (1 << j);
}
private:
vector<int> _bits;
};
template<size_t N>
class two_bit_set
{
public:
void set(size_t x)
{
if (b1.test(x) == false && b2.test(x) == false)
{
b2.set(x);
}
else if (b1.test(x) == false && b2.test(x) == true)
{
b1.set(x);
b2.reset(x);
}
}
//检测只出现一次的数
bool testone(size_t x)
{
if (b1.test(x) == false && b2.test(x)==true)
{
return true;
}
return false;
}
private:
bitset<N> b1;
bitset<N> b2;
};
}1.2位图应用
二、布隆过滤器
当我们在各大游戏或社交平台注册账号时,有的平台昵称往往是不允许重复的,那当输入昵称时,系统是如何立马就能进行判断查找出是否存在重复的呢?
根据所学知识,通常可以想到两种方法:
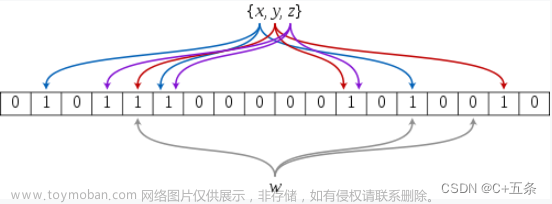
2.1布隆过滤器的原理
讲述布隆过滤器的原理之前,我们先思考一下,通常你判断某个元素是否存在用的是什么?应该大多数人会回答 HashMap 吧,确实可以将值映射到 HashMap 的 Key,然后可以在 O(1) 的时间复杂度内返回结果,效率奇高。但是 HashMap 的实现也有缺点,例如存储容量占比高,考虑到负载因子的存在,通常空间是不能被用满的,而一旦你的值很多例如上亿的时候,那 HashMap 占据的内存大小就变得很可观了。
还比如说你的数据集存储在远程服务器上,本地服务接受输入,而数据集非常大不可能一次性读进内存构建 HashMap 的时候,也会存在问题。
2.2布隆过滤器的查找

布隆过滤器是一个 bit 向量或者说 bit 数组,如果我们要映射一个值到布隆过滤器中,我们需要使用多个不同的哈希函数生成多个哈希值,并对每个生成的哈希值指向的 bit 位置 1,例如针对值 “C+五条” 通过三个不同的哈希函数分别生成了哈希值 1、4、7,则上图转变为:

我们现在再存一个值 “CSDN”,如果哈希函数返回 3、4、8 的话,图继续变为:

值得注意的是,4 这个 bit 位由于两个值的哈希函数都返回了这个 bit 位,因此它被覆盖了。现在我们如果想查询 “dianping” 这个值是否存在,哈希函数返回了 1、5、8三个值,结果我们发现 5 这个 bit 位上的值为 0,说明没有任何一个值映射到这个 bit 位上,因此我们可以很确定地说 “dianping” 这个值不存在。而当我们需要查询 “C+五条” 这个值是否存在的话,那么哈希函数必然会返回 1、4、7,然后我们检查发现这三个 bit 位上的值均为 1,那么我们可以说 “C+五条” 存在了么?答案是不可以,只能是 “C+五条” 这个值可能存在。
这是为什么呢?答案跟简单,因为随着增加的值越来越多,被置为 1 的 bit 位也会越来越多,这样某个值 “taobao” 即使没有被存储过,但是万一哈希函数返回的三个 bit 位都被其他值置位了 1 ,那么程序还是会判断 “taobao” 这个值存在。
2.2布隆过滤器的删除
2.3如何选择哈希函数个数和布隆过滤器长度
很显然,过小的布隆过滤器很快所有的 bit 位均为 1,那么查询任何值都会返回“可能存在”,起不到过滤的目的了。布隆过滤器的长度会直接影响误报率,布隆过滤器越长其误报率越小。
另外,哈希函数的个数也需要权衡,个数越多则布隆过滤器 bit 位置位 1 的速度越快,且布隆过滤器的效率越低;但是如果太少的话,那我们的误报率会变高。

k 为哈希函数个数,m 为布隆过滤器长度,n 为插入的元素个数,p 为误报率 文章来源:https://www.toymoban.com/news/detail-848089.html
三、布隆过滤器的实现
#pragma once
#include<bitset>
#include<string>
#include<iostream>
using namespace std;
struct HashFuncBKDR//第一个哈希函数
{
// BKDR
size_t operator()(const string& s)
{
size_t hash = 0;
for (auto ch : s)
{
hash *= 131;
hash += ch;
}
return hash;
}
};
struct HashFuncAP//第二个哈希函数
{
// AP
size_t operator()(const string& s)
{
size_t hash = 0;
for (size_t i = 0; i < s.size(); i++)
{
if ((i & 1) == 0) // 偶数位字符
{
hash ^= ((hash << 7) ^ (s[i]) ^ (hash >> 3));
}
else // 奇数位字符
{
hash ^= (~((hash << 11) ^ (s[i]) ^ (hash >> 5)));
}
}
return hash;
}
};
struct HashFuncDJB//第三个哈希函数
{
// DJB
size_t operator()(const string& s)
{
size_t hash = 5381;
for (auto ch : s)
{
hash = hash * 33 ^ ch;
}
return hash;
}
};
template<size_t N,
class K=string,
class Hash1 = HashFuncBKDR,
class Hash2 = HashFuncAP,
class Hash3 = HashFuncDJB>
class bloomfilter
{
public:
void set(const K& key)
{
size_t hash1 = Hash1()(key) % M;
size_t hash2 = Hash2()(key) % M;
size_t hash3 = Hash3()(key) % M;
_bs->set(hash1);
_bs->set(hash2);
_bs->set(hash3);
}
bool Test(const K& key)
{
size_t hash1 = Hash1()(key) % M;
if (_bs->test(hash1) == false)
return false;
size_t hash2 = Hash2()(key) % M;
if (_bs->test(hash2) == false)
return false;
size_t hash3 = Hash3()(key) % M;
if (_bs->test(hash3) == false)
return false;
return true; // 存在误判(有可能3个位都是跟别人冲突的,所以误判)
}
private:
static const size_t M = 10 * N;
std::bitset<M>* _bs = new std::bitset<M>;
};
布隆过滤器的优缺点
优点:文章来源地址https://www.toymoban.com/news/detail-848089.html
到了这里,关于C++哈希hash:位图、布隆过滤器的实现及应用的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!


![[C++]哈希应用之位图&布隆过滤器](https://imgs.yssmx.com/Uploads/2024/04/852662-1.gif)