Android OpenCV（三十七）：轮廓外接多边形

这篇具有很好参考价值的文章主要介绍了Android OpenCV（三十七）：轮廓外接多边形。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

参数四：closed，逼近曲线是否闭合的标志，true表示封闭，false，表示不封闭。

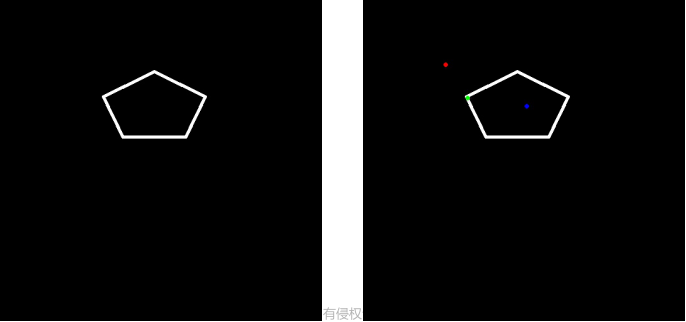
该方法使用的是Douglas-Peucker algorithm（道格拉斯-普克算法）。Douglas-Peukcer算法由D.Douglas和T.Peueker于1973年提出，也称为拉默-道格拉斯-普克算法、迭代适应点算法、分裂与合并算法、D-P算法)是将曲线近似表示为一系列点，并减少点的数量的一种算法，是线状要素抽稀的经典算法。用它处理大量冗余的几何数据点，既可以达到数据量精简的目的，又可以在很大程度上保留几何形状的骨架。现有的线化简算法中，有相当一部分都是在该算法基础上进行改进产生的。它的特点是具有平移和旋转不变性，给定曲线与阈值后，抽样结果一定。

算法的基本思路为：

对每一条曲线的首末点虚连一条直线，求所有点与直线的距离，并找出最大距离值dmax，用dmax与限差D相比：若dmax＜D，这条曲线上的中间点全部舍去；若dmax≥D，保留dmax对应的坐标点，并以该点为界，把曲线分为两部分，对这两部分重复使用该方法

操作

/**

轮廓外接多边形
author: yidong
2020/10/7
*/
class ContourPolyActivity : AppCompatActivity() {

private lateinit var mBinding: ActivityContourPolyBinding
private var mSource: Mat = Mat()
private var mGray: Mat = Mat()
private var mBinary: Mat = Mat()

override fun onCreate(savedInstanceState: Bundle?) {
super.onCreate(savedInstanceState)
mBinding = DataBindingUtil.setContentView(this, R.layout.activity_contour_poly)
mBinding.presenter = this
val bgr = Utils.loadResource(this, R.drawable.contourpoly)
Imgproc.cvtColor(bgr, mSource, Imgproc.COLOR_BGR2RGB)
Imgproc.cvtColor(bgr, mGray, Imgproc.COLOR_BGR2GRAY)
Imgproc.GaussianBlur(mGray, mGray, Size(5.0, 5.0), 2.0, 2.0)
Imgproc.threshold(
mGray,
mBinary,
20.0,
255.0,
Imgproc.THRESH_BINARY or Imgproc.THRESH_OTSU
)
mBinding.ivLena.showMat(mBinary)
}

fun findRect(flag: Int) {
val tmp = mSource.clone()
val contours = mutableListOf()
val hierarchy = Mat()
Imgproc.findContours(
mBinary,
contours,
hierarchy,
Imgproc.RETR_TREE,
Imgproc.CHAIN_APPROX_SIMPLE
)

for (i in 0 until contours.size) {
when (flag) {
0 -> {
title = “最大外接矩形”
val rect = Imgproc.boundingRect(contours[i])
Imgproc.rectangle(tmp, rect, Scalar(255.0, 255.0, 0.0), 4, Imgproc.LINE_8)
}
1 -> {
title = “最小外接矩形”
val source = MatOfPoint2f()
source.fromList(contours[i].toList())
val rect = Imgproc.minAreaRect(source)
val points = arrayOfNulls(4)
val center = rect.center
rect.points(points)
Log.d(App.TAG, “RotateRect: ${points.toList()}, Center：$ center”)
for (j in 0…3) {
Imgproc.line(
tmp,
points[j % 4],
points[(j + 1) % 4],
Scalar(255.0, 255.0, 0.0),
4,
Imgproc.LINE_8
)
}
}
else -> {
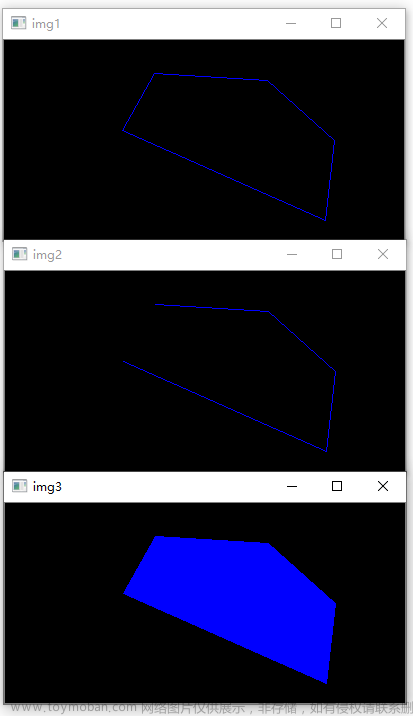
title = “轮廓多边形”
val result = MatOfPoint2f()
val source = MatOfPoint2f()
source.fromList(contours[i].toList())
Imgproc.approxPolyDP(source, result, 4.0, true)
Log.d(App.TAG, “Poly: ${result.dump()}”)
val points = result.toArray()
for (j in points.indices) {
Imgproc.line(
tmp,
points[j % points.size],
points[(j + 1) % points.size],
Scalar(255.0, 255.0, 0.0),
4,
Imgproc.LINE_8
)
}
}
}
}
mBinding.ivResult.showMat(tmp)
tmp.release()
hierarchy.release()
}