概率论与深度学习：从简单到复杂

这篇具有很好参考价值的文章主要介绍了概率论与深度学习：从简单到复杂。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1.背景介绍

深度学习是一种人工智能技术，它旨在让计算机模仿人类的智能。概率论是数学的一个分支，它用于描述不确定性和随机性。深度学习和概率论之间的关系非常紧密，因为深度学习模型需要处理大量的随机数据，并且需要使用概率论来描述和优化这些模型。

在这篇文章中，我们将从简单的概率论概念开始，逐步深入到深度学习的核心算法和实例。我们将讨论概率论和深度学习之间的关系，并探讨它们在实际应用中的挑战和未来发展趋势。

2.核心概念与联系

2.1 概率论基础

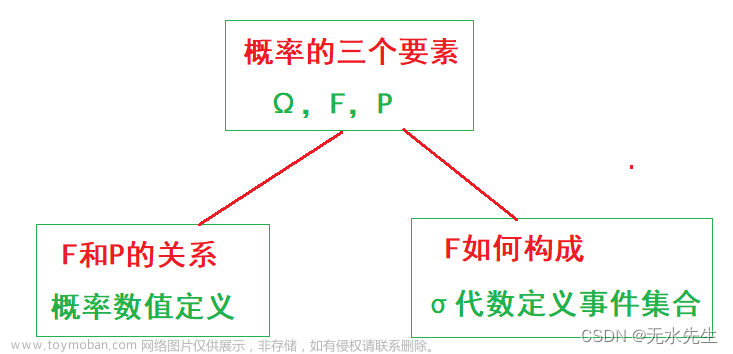
概率论是一种数学方法，用于描述和分析不确定性和随机性。概率论的基本概念包括事件、样本空间、事件的概率和条件概率。

2.1.1 事件和样本空间

事件是一个可能发生的结果，样本空间是所有可能结果的集合。例如，在一场六面骰子的掷子中，样本空间是{1, 2, 3, 4, 5, 6}，掷出“3”的事件是样本空间中的一个元素。

2.1.2 概率

概率是一个事件发生的可能性，通常用[0, 1]间的一个数来表示。例如，在一场六面骰子的掷子中，掷出“3”的概率是1/6。

2.1.3 条件概率

条件概率是一个事件发生的可能性，给定另一个事件已发生的情况下。例如，在一场六面骰子的掷子中，掷出“3”并且“偶数”的条件概率是1/3。

2.2 深度学习基础

深度学习是一种人工智能技术，它旨在让计算机模仿人类的智能。深度学习的核心概念包括神经网络、损失函数和梯度下降。

2.2.1 神经网络

神经网络是深度学习的基本结构，它由多个节点(神经元)和连接这些节点的权重组成。神经网络可以学习从输入到输出的映射关系，以便在新的输入数据上进行预测。

2.2.2 损失函数

损失函数是用于衡量模型预测与实际值之间差距的函数。损失函数的目标是最小化这个差距，以便优化模型的性能。

2.2.3 梯度下降

梯度下降是一种优化算法，用于最小化损失函数。梯度下降算法通过迭代地更新模型的参数，以便逐步减少损失函数的值。

3.核心算法原理和具体操作步骤以及数学模型公式详细讲解

3.1 概率论的核心算法

3.1.1 贝叶斯定理

贝叶斯定理是概率论的一个重要定理，它描述了给定新的信息后，原有概率的更新。贝叶斯定理的数学表达式为：

$$ P(A|B) = \frac{P(B|A)P(A)}{P(B)} $$

其中，$P(A|B)$ 是给定$B$已发生的情况下，$A$发生的概率；$P(B|A)$ 是给定$A$发生的情况下，$B$发生的概率；$P(A)$ 是$A$发生的概率；$P(B)$ 是$B$发生的概率。

3.1.2 条件独立性

条件独立性是概率论的一个重要概念，它描述了两个事件在给定其他事件已发生的情况下，是否相互独立。条件独立性的数学表达式为：

$$ P(A \cap B|C) = P(A|C)P(B|C) $$

其中，$P(A \cap B|C)$ 是给定$C$已发生的情况下，$A$和$B$发生的概率；$P(A|C)$ 是给定$C$已发生的情况下，$A$发生的概率；$P(B|C)$ 是给定$C$已发生的情况下，$B$发生的概率。

3.2 深度学习的核心算法

3.2.1 前向传播

前向传播是深度学习模型的一个核心操作，它用于计算输入数据通过神经网络的每个节点的输出。前向传播的数学表达式为：

$$ zj^{(l)} = \sum{i} w{ij}^{(l-1)}xi^{(l-1)} + b_j^{(l)} $$

$$ aj^{(l)} = f(zj^{(l)}) $$

其中，$zj^{(l)}$ 是第$l$层第$j$节点的输入；$w{ij}^{(l-1)}$ 是第$l-1$层第$i$节点到第$l$层第$j$节点的权重；$xi^{(l-1)}$ 是第$l-1$层第$i$节点的输出；$bj^{(l)}$ 是第$l$层第$j$节点的偏置；$a_j^{(l)}$ 是第$l$层第$j$节点的输出；$f$ 是一个激活函数。

3.2.2 后向传播

后向传播是深度学习模型的另一个核心操作，它用于计算输入数据通过神经网络的每个节点的梯度。后向传播的数学表达式为：

$$ \deltaj^{(l)} = \frac{\partial L}{\partial zj^{(l)}} \cdot f'(z_j^{(l)}) $$

$$ \frac{\partial w{ij}^{(l)}}{\partial L} = \deltaj^{(l)}x_i^{(l-1)} $$

$$ \frac{\partial b{j}^{(l)}}{\partial L} = \deltaj^{(l)} $$

其中，$\deltaj^{(l)}$ 是第$l$层第$j$节点的梯度；$f'$ 是一个激活函数的导数；$\frac{\partial w{ij}^{(l)}}{\partial L}$ 是第$l$层第$i$节点到第$l$层第$j$节点的权重关于损失函数的梯度；$\frac{\partial b_{j}^{(l)}}{\partial L}$ 是第$l$层第$j$节点的偏置关于损失函数的梯度；$L$ 是损失函数。

3.2.3 梯度下降

梯度下降是深度学习模型的一个核心操作，它用于优化模型的参数。梯度下降的数学表达式为：

$$ w{ij} = w{ij} - \eta \frac{\partial L}{\partial w_{ij}} $$

其中，$w{ij}$ 是第$i$节点到第$j$节点的权重；$\eta$ 是学习率；$\frac{\partial L}{\partial w{ij}}$ 是第$i$节点到第$j$节点的权重关于损失函数的梯度。

4.具体代码实例和详细解释说明

在这里，我们将通过一个简单的深度学习示例来解释上述算法的实际应用。我们将使用Python的TensorFlow库来实现这个示例。

```python import tensorflow as tf

定义一个简单的神经网络

class SimpleNet(tf.keras.Model): def init(self): super(SimpleNet, self).init() self.dense1 = tf.keras.layers.Dense(64, activation='relu') self.dense2 = tf.keras.layers.Dense(10, activation='softmax')

def call(self, inputs, training=False):
    x = self.dense1(inputs)
    return self.dense2(x)

创建一个简单的数据集

(xtrain, ytrain), (xtest, ytest) = tf.keras.datasets.mnist.loaddata() xtrain = xtrain / 255.0 xtest = x_test / 255.0

创建一个简单的神经网络实例

model = SimpleNet()

编译模型

model.compile(optimizer=tf.keras.optimizers.Adam(learningrate=0.001), loss='sparsecategorical_crossentropy', metrics=['accuracy'])

训练模型

model.fit(xtrain, ytrain, epochs=5)

评估模型

testloss, testacc = model.evaluate(xtest, ytest) print('Test accuracy:', test_acc) ```

在这个示例中，我们首先定义了一个简单的神经网络类SimpleNet，它包括一个relu激活函数的全连接层和一个softmax激活函数的输出层。然后，我们创建了一个简单的数据集mnist，并将其分为训练集和测试集。接下来，我们创建了一个SimpleNet实例，并使用Adam优化器和稀疏类别交叉Entropy损失函数来编译模型。最后，我们训练模型并评估其在测试集上的准确率。

5.未来发展趋势与挑战

深度学习和概率论的未来发展趋势包括更高效的优化算法、更强大的神经网络架构和更好的解释性和可解释性。挑战包括数据不可知性、模型复杂性和计算资源限制。

6.附录常见问题与解答

在这里，我们将列出一些常见问题和解答，以帮助读者更好地理解概率论和深度学习的相关概念。

问题1：什么是梯度下降？

答案：梯度下降是一种优化算法，用于最小化损失函数。梯度下降算法通过迭代地更新模型的参数，以便逐步减少损失函数的值。

问题2：什么是贝叶斯定理？

答案：贝叶斯定理是概率论的一个重要定理，它描述了给定新的信息后，原有概率的更新。贝叶斯定理的数学表达式为：

$$ P(A|B) = \frac{P(B|A)P(A)}{P(B)} $$

问题3：什么是条件独立性？

答案：条件独立性是概率论的一个重要概念，它描述了两个事件在给定其他事件已发生的情况下，是否相互独立。条件独立性的数学表达式为：

$$ P(A \cap B|C) = P(A|C)P(B|C) $$

问题4：什么是损失函数？

答案：损失函数是用于衡量模型预测与实际值之间差距的函数。损失函数的目标是最小化这个差距，以便优化模型的性能。

问题5：什么是激活函数？

答案：激活函数是深度学习模型中的一个重要组件，它用于引入非线性性。激活函数的常见类型包括relu、sigmoid和tanh等。

问题6：什么是过拟合？

答案：过拟合是深度学习模型的一个常见问题，它发生在模型过于复杂，导致在训练数据上的表现很好，但在新的数据上的表现很差。为了避免过拟合，可以使用正则化、减少模型的复杂性等方法。文章来源地址https://www.toymoban.com/news/detail-856754.html

到了这里，关于概率论与深度学习：从简单到复杂的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

Toy模板网