3.5.4、根据 Epic 近似假设进一步拆分积分项为两部分之积
通过之前的步骤,实际上以及得到了我们想要的镜面反射项的蒙特卡洛积分重要性采样的形式,并且根据我们的假设认为视方向等于法线方向,实际上以及可以编码实现这个积分计算过程,而且依据假设我们不再需要额外的参数了,那么这个积分项实际上也是可以进行预积分的,无非就是需要根据不同的粗糙度、以及菲涅尔系数,生成一系列的预积分贴图供后续的渲染循环中采样使用。
但是因为粗糙度系数是范围为 [ 0 , 1 ] [0,1] [0,1] 之间的连续数,而且菲涅尔系数是根据不同的材质有一个较大的向量表示的范围,所以这时预积分或者说为了把镜面反射项也像漫反射积分项那样简单的预积分的话,还是困难重重的。
所以为了进一步简化其计算,Epic Game 在 Unreal 引擎索性先做了如下的近似拆分:
L
o
s
(
p
⃗
,
ω
o
⃗
)
≈
1
N
∑
n
=
1
N
F
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
L
i
(
p
⃗
)
≈
1
N
∑
n
=
1
N
F
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
×
1
N
∑
n
=
1
N
L
i
(
p
⃗
)
\mathrm{L}_{o_s}(\vec{p},\vec{\omega_{o}}) \approx \cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{FG\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} \mathrm{L}_i(\vec{p}) \\[2ex] \approx \cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{FG\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} \times \cfrac{1}{N} \sum \limits_{n=1}^{N} \mathrm{L}_i(\vec{p})
Los(p,ωo)≈N1n=1∑N(ωo⋅n)×(n⋅h)FG×(ωo⋅h)Li(p)≈N1n=1∑N(ωo⋅n)×(n⋅h)FG×(ωo⋅h)×N1n=1∑NLi(p)
啊哈!真的是一个脑洞大开的假设!这样的近似,其实就是将所有的入射辐照度
L
i
(
p
⃗
)
L_i(\vec{p})
Li(p) 取平均,然后看做是一个单位大小的标准辐照度,然后剩下的前半部分的求和就是 BRDF 在标准单位辐照度情况下的响应系数。这就好像,我们买了很多菜,为了算出每种菜的花费,直接将所有的菜不加区分的先按重量求和然后按品种平均之后,再与所有菜价按种类取平均后相乘,就大致得到了每种菜的花费,它与每种菜的实际花费是比较相近的。希望你能看明白我在说什么。
这样拆分后,会有很多好处,主要是下面两点:
1、乘积的第1项可以依据 BRDF 的近似解析式进一步拆分出可以预计算的部分,从而经过前面的这些拆分预计算过程后,在真正的渲染循环中在物体表面每个点上的计算量就大大减少,最终可以实现质量和效率兼顾的 PBR 渲染!
2、乘积的第2项,基本就是环境映射贴图的一个简单采样而已,省却了很多复杂计算;和“漫反射项”一样基本上都可以被提出渲染循环,进行一次性计算(或称之为预计算)!
3.5.5、镜面反射预过滤积分贴图的重要性采样实现
这样做了之后的好处就是,可以先简单的按照重要性采样方法来计算其中的第二部分,此时我们观察下重要性采样时,我们需要生成的随机变量:
θ
h
=
arccos
(
1
−
μ
μ
(
α
2
−
1
)
+
1
)
,
ϕ
h
=
2
π
ν
\theta_h = \arccos \left( \sqrt{\cfrac{1-\mu}{\mu (\alpha^2 - 1 ) + 1}} \right) , \quad \phi_h = 2 \pi \nu
θh=arccos
μ(α2−1)+11−μ
,ϕh=2πν
此时我们发现,根据球坐标转换为笛卡尔坐标的公式,生成的随机向量实际是
h
⃗
\vec{h}
h ,而我们需要的采样的向量却是入射光的方向向量
ω
⃗
i
\vec{\omega}_i
ωi 。此时根据中间向量的定义,我们有
ω
⃗
i
=
2
×
(
ω
⃗
o
⋅
h
⃗
)
×
h
⃗
−
ω
⃗
o
\vec{\omega}_i = 2 \times (\vec{\omega}_o \cdot \vec{h}) \times \vec{h} - \vec{\omega}_o
ωi=2×(ωo⋅h)×h−ωo ,这个公式中我们还需要知道视见方向
ω
⃗
o
\vec{\omega}_o
ωo , 这在我们前面推导的过程中,假设
ω
⃗
o
\vec{\omega}_o
ωo 就等于平面的法线方向
n
⃗
\vec{n}
n,所以生成了中间向量
h
⃗
\vec{h}
h,就可以解算出入射光方向
ω
⃗
i
\vec{\omega}_i
ωi。
同时我们还发现,与预计算的漫反射辐照度贴图中用的随机变量不同,主要是 θ h \theta_h θh 变量有区别,其中还有与粗糙度相关的参数 α = r o u g h n e s s 2 , r o u g h n e s s ∈ [ 0.0 , 1.0 ] \alpha = roughness^2,roughness \in [0.0,1.0] α=roughness2,roughness∈[0.0,1.0] ,也就是与粗糙度的平方相关联,所以不能像漫反射辐照度贴图那样简单的生成 。
此时通常的做法就是取一些相对离散的粗糙度参数 (
r
o
u
g
h
n
e
s
s
roughness
roughness )的值,来生成多幅不同的环境映射贴图,然后根据最接近的粗糙度参数采样不同的贴图即可。通常这可以通过纹理的 Map Level 参数来做到,我们可以定义:
r
o
u
g
h
n
e
s
s
=
M
a
p
L
e
v
e
l
M
a
p
L
e
v
e
l
C
o
u
n
t
roughness = \cfrac{MapLevel}{MapLevelCount}
roughness=MapLevelCountMapLevel
来计算不同 MapLevel ,也就是不同 roughness 离散值的贴图。
当然如果你需要近可能高质量的镜面反射预过滤积分贴图的话,可以考虑使用 3D Texture 来做,此时3D纹理坐标(u,v,w)中的 w 坐标就可以被用作 roughness 参数。只是这样一来,需要的存储空间,以及计算量就增大了一个量级,而实际的效果可能比用MapLevel方式好不到哪里去,也就是很可能是得不偿失的。
在本章示例代码的 Shader 文件 GRSD3D12Sample/GRS_PBR_Function.hlsli 中实现的产生随机采样向量的方法如下:
float3 ImportanceSampleGGX(float2 Xi, float3 N, float roughness)
{
float a = roughness * roughness;
float phi = 2.0f * PI * Xi.x;
float cosTheta = sqrt((1.0f - Xi.y) / (1.0f + (a * a - 1.0f) * Xi.y));
float sinTheta = sqrt(1.0f - cosTheta * cosTheta);
float3 H;
H.x = cos(phi) * sinTheta;
H.y = sin(phi) * sinTheta;
H.z = cosTheta;
float3 up = abs(N.z) < 0.999 ? float3(0.0f, 0.0f, 1.0f) : float3(1.0f, 0.0f, 0.0f);
float3 tangent = normalize(cross(up, N));
float3 bitangent = cross(N, tangent);
float3 sampleVec = tangent * H.x + bitangent * H.y + N * H.z;
return normalize(sampleVec);
}
并且在生成镜面反射预过滤积分贴图的 Shader 文件中,实现如下:
float4 PSMain(ST_GRS_HLSL_PS_INPUT pin) : SV_Target
{
float3 N = normalize(pin.m_v4WPos.xyz);
float3 R = N;
float3 V = R;
uint SAMPLE_COUNT = GRS_INT_SAMPLES_CNT;
float3 prefilteredColor = float3(0.0f, 0.0f, 0.0f);
float totalWeight = 0.0f;
for (uint i = 0; i < SAMPLE_COUNT; ++i)
{
// 生成均匀分布的无偏序列(Hammersley)
float2 Xi = Hammersley(i, SAMPLE_COUNT);
// 进行有偏的重要性采样
float3 H = ImportanceSampleGGX(Xi, N, g_fRoughness);
float3 L = normalize(2.0f * dot(V, H) * H - V);
float NdotL = max(dot(N, L), 0.0f);
if ( NdotL > 0.0f )
{
prefilteredColor += g_texHDREnvCubemap.Sample(g_sapLinear, L).rgb * NdotL;
totalWeight += NdotL;
}
}
prefilteredColor = prefilteredColor / totalWeight;
return float4(prefilteredColor, 1.0f);
}
上面两段代码已经是严格按照我们数学推导的过程而实现的,如果数学推导过程搞明白了,那么这些代码就没有什么难以理解的了,甚至你应该有一种豁然开朗的感觉了。再去看 UE 的 Shader 实现也应该没什么难度了,一切都是 So easy!
上面代码中唯一需要注意的地方就是在最终采样的函数代码中计算了 NdotL 的值,并且以它的和作为最后积分平均的分母项,主要是因为在粗糙度比较大的时候,根据 h ⃗ \vec{h} h 解算的 ω ⃗ i \vec{\omega}_i ωi 有可能会到半球平面的背后去,这是因为此时我们假设的视见向量在法线方向。这对于我们现在计算的不透明物体表面的反射来说是不合理的,此时就用 NdotL 的值作为权重值,来最终平均求和的值。其原理就是我在博文 3D数学系列之——从“蒙的挺准”到“蒙的真准”解密蒙特卡洛积分! 中说的蒙特卡洛积分的第一种“数小点点”的方法,过滤后的NdotL值的和,正好是出现在反射面正面中的 ω ⃗ i \vec{\omega}_i ωi 的比例值。
在本章代码中,设定了镜面反射预过滤积分贴图的 MaxMapLevel = 5 , 然后因为是以CubeMap的形式存储最终结果,所以需要存储不同的6个面,最终就需要总共 5*6 = 30幅 2D Texture,这样整个预积分贴图需要的显存量还是巨大的。
当然如果只是 Demo 演示程序来说这不是问题,但是在正式工程项目中,场景不止一个,同时还需要按照不同的 probe 来生成多幅预积分贴图时,就不得不考虑纹理压缩以及简化存储的问题了。希望将来有机会我们可以继续探讨这个问题。
最终在示例代码运行后显示的小矩形中,完整的按MapLevel顺序优先的方式展现了这30幅纹理的样子:
这中间有个细节问题,就是说如果预积分过滤贴图是从最原始的高分辨率直接采样到对应低分辨率MapLevel贴图上时可能会产生一些高频噪声,但在本章示例中还没有遇到这种情况,所以就先不搭理了。那么更一般的做法是说先将环境纹理按照对应的MapLevel预生成一下MipMap,然后再来采样生成镜面反射的预积分贴图,因为我比较懒就没有这样做了。反正看上去是对的就行!
3.5.6、菲涅尔近似项 F S c h l i c k F_{Schlick} FSchlick 中菲涅尔常数 F 0 F_0 F0 的分离
处理完镜面反射项的预过滤积分贴图后,我们接着来看被分离出的 BRDF 项:
1
N
∑
n
=
1
N
F
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
\cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{FG\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})}
N1n=1∑N(ωo⋅n)×(n⋅h)FG×(ωo⋅h)
其中 F 和 G 函数除了与参与整个计算的向量
h
⃗
,
n
⃗
,
ω
⃗
i
,
ω
⃗
o
\vec{h},\vec{n},\vec{\omega}_i,\vec{\omega}_o
h,n,ωi,ωo 有关外,还与两个常数参数
F
0
,
r
o
u
g
h
n
e
s
s
F_0,roughness
F0,roughness 有关,如果要进行预计算,那么就还需要一些简化工作,尤其是对菲涅尔系数
F
0
F_0
F0 来说,我们基本上不太可能预生成它全部的取值。因为实际中,我们将颜色表示为 RGB 分量的形式(或者说辐射能量被我们以RGB向量的形式给离散化了),导致菲涅尔系数也被离散向量化了,所以要枚举它全部可能的取值,是不太现实的。
此时在 Unreal 引擎中,对函数 F 项做了进一步的拆分。首先我们来回顾下 “Cook-Torrance” 模型 BRDF 函数中的菲涅尔项的近似表达式(Scklinck近似):
F
=
F
S
c
h
l
i
c
k
(
h
⃗
,
v
⃗
,
F
0
)
=
F
0
+
(
1
−
F
0
)
(
1
−
(
h
⃗
⋅
v
⃗
)
)
5
F = F_{Schlick}(\vec{h},\vec{v},F_0) = F_0 + ( 1 - F_0 )(1 - (\vec{h} \cdot \vec{v}))^5
F=FSchlick(h,v,F0)=F0+(1−F0)(1−(h⋅v))5
式中 “
F
0
F_0
F0 ” 项对于要渲染的物体上的一点
p
⃗
\vec{p}
p 来说往往是个常数,并且这个表达式是个和形式,此时我们考虑将这个常数项从其中提取出来并做一下整理(基本就是初中数学知识的应用):
F
=
F
S
c
h
l
i
c
k
(
h
⃗
,
v
⃗
,
F
0
)
=
F
0
+
(
1
−
F
0
)
(
1
−
(
h
⃗
⋅
v
⃗
)
)
5
=
F
0
+
(
1
−
(
h
⃗
⋅
v
⃗
)
)
5
−
F
0
(
1
−
(
h
⃗
⋅
v
⃗
)
)
5
=
F
0
(
1
−
(
1
−
(
h
⃗
⋅
v
⃗
)
)
5
)
+
(
1
−
(
h
⃗
⋅
v
⃗
)
)
5
F = F_{Schlick}(\vec{h},\vec{v},F_0) = F_0 + ( 1 - F_0 )(1 - (\vec{h} \cdot \vec{v}))^5 \\[2ex] = F_0 + (1 - (\vec{h} \cdot \vec{v}))^5 - F_0(1 - (\vec{h} \cdot \vec{v}))^5 \\[2ex] = F_0 ( 1- (1 - (\vec{h} \cdot \vec{v}))^5 ) + (1 - (\vec{h} \cdot \vec{v}))^5
F=FSchlick(h,v,F0)=F0+(1−F0)(1−(h⋅v))5=F0+(1−(h⋅v))5−F0(1−(h⋅v))5=F0(1−(1−(h⋅v))5)+(1−(h⋅v))5
然后将上式中这个结果再代回到镜面反射蒙特卡洛积分拆分后的 BRDF 积分项中有:
1
N
∑
n
=
1
N
F
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
=
1
N
∑
n
=
1
N
(
F
0
(
1
−
(
1
−
(
h
⃗
⋅
v
⃗
)
)
5
)
+
(
1
−
(
h
⃗
⋅
v
⃗
)
)
5
)
×
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
=
F
0
1
N
∑
n
=
1
N
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
(
1
−
(
1
−
ω
o
⃗
⋅
h
⃗
)
5
)
⏟
P
a
r
t
(
1
)
+
1
N
∑
n
=
1
N
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
(
1
−
ω
o
⃗
⋅
h
⃗
)
5
⏟
P
a
r
t
(
2
)
\cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{FG\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} \\[2ex] = \cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{\Bigl(F_0 ( 1- (1 - (\vec{h} \cdot \vec{v}))^5 ) + (1 - (\vec{h} \cdot \vec{v}))^5 \Bigr) \times G \times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} \\[2ex] = F_0 \underbrace{\cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{G\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} (1 - ( 1-\vec{\omega_o} \cdot \vec{h} ) ^5) }_{Part(1)} \\[2ex] + \underbrace{\cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{G\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} ( 1-\vec{\omega_o} \cdot \vec{h} ) ^5 }_{Part(2)}
N1n=1∑N(ωo⋅n)×(n⋅h)FG×(ωo⋅h)=N1n=1∑N(ωo⋅n)×(n⋅h)(F0(1−(1−(h⋅v))5)+(1−(h⋅v))5)×G×(ωo⋅h)=F0Part(1)
N1n=1∑N(ωo⋅n)×(n⋅h)G×(ωo⋅h)(1−(1−ωo⋅h)5)+Part(2)
N1n=1∑N(ωo⋅n)×(n⋅h)G×(ωo⋅h)(1−ωo⋅h)5
从上面的推导过程可以看出,不但
F
0
F_0
F0 被我们从求和中提取了出来,而且最终求和又变成了两个很相似的部分。回忆一下整个过程,这正如《道德经》中所说:“道生一,一生二,二生三,三生万物。万物负阴而抱阳,冲气以为和。” 负阴而抱阳正好就是我们开初的假设:渲染的是不透明的物体,所有的反射都在其表面发生。
而上式中的这个拆分,尤其是提取出了菲涅尔系数的结果,恰恰反过来说明,为什么实时 PBR 在一开始设计近似 BRDF 函数时,选择了菲涅尔函数的 Scklinck 近似的原因,就是为了最后能把这个恼人的 F 0 F_0 F0 系数从积分求和的过程中完全提取出来,成为一个参数,使得最后的蒙特卡洛积分的 BRDF 部分也能够变成预计算项,而不用出现在渲染循环中,这使得整个实时 PBR 渲染可以高效运行,并且保持一定的质量精度成为可能。
3.5.7、预积分 BRDF-LUT贴图
至此镜面反射蒙特卡洛积分项中,就只剩下一个被称之为微表面几何函数的项
G
G
G ,它的最终表达式如下:
G
S
c
h
l
i
c
k
G
G
X
(
n
⃗
,
ω
⃗
,
κ
)
=
n
⃗
⋅
ω
⃗
(
n
⃗
⋅
ω
⃗
)
(
1
−
κ
)
+
κ
κ
d
i
r
e
c
t
=
(
α
+
1
)
2
8
κ
I
B
L
=
α
2
2
G
(
n
⃗
,
ω
o
⃗
,
ω
i
⃗
,
κ
)
=
G
S
c
h
l
i
c
k
G
G
X
(
n
⃗
,
ω
o
⃗
,
κ
)
G
S
c
h
l
i
c
k
G
G
X
(
n
⃗
,
ω
i
⃗
,
κ
)
上列式子中:
α
=
r
o
u
g
h
n
e
s
s
2
r
o
u
g
h
n
e
s
s
∈
[
0.0
,
1.0
]
(粗糙度系数)
G_{SchlickGGX}(\vec{n},\vec{\omega},\kappa) = \frac{\vec{n} \cdot \vec{\omega}}{(\vec{n} \cdot \vec{\omega})(1-\kappa) + \kappa } \\[2ex] \kappa_{direct} = \frac{(\alpha + 1)^2}{8} \\[2ex] \kappa_{IBL} = \frac{\alpha^2}{2} \\[2ex] G(\vec{n},\vec{\omega_o},\vec{\omega_i},\kappa) = G_{SchlickGGX}(\vec{n},\vec{\omega_o},\kappa) G_{SchlickGGX}(\vec{n},\vec{\omega_i},\kappa) \\[2ex] 上列式子中:\alpha = roughness^2 \qquad roughness \in [ \ 0.0,1.0 \ ] (粗糙度系数)
GSchlickGGX(n,ω,κ)=(n⋅ω)(1−κ)+κn⋅ωκdirect=8(α+1)2κIBL=2α2G(n,ωo,ωi,κ)=GSchlickGGX(n,ωo,κ)GSchlickGGX(n,ωi,κ)上列式子中:α=roughness2roughness∈[ 0.0,1.0 ](粗糙度系数)
结合前面推出的结果,现在我们知道下面这些量是可以计算的:
θ
h
=
arccos
(
1
−
μ
μ
(
α
2
−
1
)
+
1
)
ϕ
h
=
2
π
ν
h
⃗
=
[
sin
(
θ
h
)
cos
(
ϕ
h
)
sin
(
θ
h
)
sin
(
θ
h
)
cos
(
θ
h
)
]
ω
⃗
i
=
2
×
(
ω
⃗
o
⋅
h
⃗
)
×
h
⃗
−
ω
⃗
o
\theta_h = \arccos \left( \sqrt{\cfrac{1-\mu}{\mu (\alpha^2 - 1 ) + 1}} \right) \\[2ex] \quad \phi_h = 2 \pi \nu \\[2ex] \vec{h} = \begin{bmatrix} \sin(\theta_h)\cos(\phi_h) \\ \sin(\theta_h) \sin(\theta_h) \\ \cos(\theta_h) \end{bmatrix} \\[2ex] \vec{\omega}_i = 2 \times (\vec{\omega}_o \cdot \vec{h}) \times \vec{h} - \vec{\omega}_o
θh=arccos
μ(α2−1)+11−μ
ϕh=2πνh=
sin(θh)cos(ϕh)sin(θh)sin(θh)cos(θh)
ωi=2×(ωo⋅h)×h−ωo
同时根据我们在推导
θ
h
,
θ
\theta_h,\theta
θh,θ 关系时的假设
ω
⃗
o
=
n
⃗
\vec{\omega}_o = \vec{n}
ωo=n,此时仔细观察我们已经知道的东西,会发现最终 BRDF 蒙特卡洛积分项:
B
R
D
F
i
n
t
=
F
0
1
N
∑
n
=
1
N
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
(
1
−
(
1
−
ω
o
⃗
⋅
h
⃗
)
5
)
⏟
P
a
r
t
(
1
)
+
1
N
∑
n
=
1
N
G
×
(
ω
⃗
o
⋅
h
⃗
)
(
ω
o
⃗
⋅
n
⃗
)
×
(
n
⃗
⋅
h
⃗
)
(
1
−
ω
o
⃗
⋅
h
⃗
)
5
⏟
P
a
r
t
(
2
)
BRDF_{int}= F_0 \underbrace{\cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{G\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} (1 - ( 1-\vec{\omega_o} \cdot \vec{h} ) ^5) }_{Part(1)} \\[2ex] + \underbrace{\cfrac{1}{N} \sum \limits_{n=1}^{N} \cfrac{G\times (\vec{\omega}_o \cdot \vec{h})} {( \vec{\omega_o} \cdot \vec{n} ) \times (\vec{n} \cdot \vec{h})} ( 1-\vec{\omega_o} \cdot \vec{h} ) ^5 }_{Part(2)}
BRDFint=F0Part(1)
N1n=1∑N(ωo⋅n)×(n⋅h)G×(ωo⋅h)(1−(1−ωo⋅h)5)+Part(2)
N1n=1∑N(ωo⋅n)×(n⋅h)G×(ωo⋅h)(1−ωo⋅h)5
中,几乎所有的向量都可以计算出来,并且从这些计算推导过程可以发现,几乎所有的向量都与我们最初定位的点
p
⃗
\vec{p}
p 毫无关系,或者说这些向量的计算根本就没有点
p
⃗
\vec{p}
p 的参与。
其实这从本质上来说是合理的,因为 BRDF 函数就是抽象物理光照反射过程而得到的一个通用的模型,所以它肯定是与具体的点
p
⃗
\vec{p}
p 本身无关的。基于这样的结果,在 Epic 中就做了一个更加普适性的一个假设,那就是:
n
⃗
=
(
0.0
,
0.0
,
1.0
)
\vec{n} = (0.0,0.0,1.0)
n=(0.0,0.0,1.0)
即法向量始终是正Z轴方向,这样一来所有的计算都简化了,唯一剩下的需要积分的量就是点积
ω
⃗
o
⋅
h
⃗
\vec{\omega}_o \cdot \vec{h}
ωo⋅h 了,因为它与
n
⃗
\vec{n}
n 无关,同时它还是
G
S
c
h
l
i
c
k
G_{Schlick}
GSchlick 函数中需要计算的一项。此时似乎我们又绕回了需要知道
ω
⃗
o
\vec{\omega}_o
ωo ,也就是需要知道视方向的问题,其实如果我们了解向量计算的话就会发现,无论向量
ω
⃗
o
,
h
⃗
\vec{\omega}_o ,\vec{h}
ωo,h 为何值,其点积都必然在
[
0
,
1
]
[0,1]
[0,1] 之间,因为都是单位向量,点积结果就是
cos
(
x
)
\cos(x)
cos(x) 函数的值。
这时再结合粗糙度系数 roughness 参数取值范围在 [ 0 , 1 ] [0,1] [0,1] 之间的事实,可以考虑使用这两个参数作为横纵坐标轴,然后预计算每一个点的值作成一副贴图。因为所有需要计算的变量综合前面的推导都已经可以计算了,而不需要延迟到渲染循环中。这是非常好的特性,而且对于预积分的 BRDF 贴图来说,它甚至跟场景都是无关,完全可以一次性生成,反复在任何需要的地方使用即可。
在实际使用时,根据实际的 ω ⃗ o ⋅ h ⃗ \vec{\omega}_o \cdot \vec{h} ωo⋅h 值和 roughness 值查找这个纹理即可得到我们预计算的 BRDF 积分值,因此这个预计算的BRDF贴图也被称为 2D LUT(2D 查找纹理,Lookup Texture),然后代入最开初镜面反射积分计算中,就可以得到一点 p ⃗ \vec{p} p 上的镜面反射值,最终再与我们计算的预积分辐照度贴图的采样值,按照完整的反射方程进行计算,就得到了一点上的最终光照效果。
从前面的进一步拆分可以看出,实际上需要计算两个值,即公式中标识的 Part(1)和Part(2),一般这两个值被放在纹理的 Red 和 Green 颜色通道中,所以最终它计算出来的样子是如下图: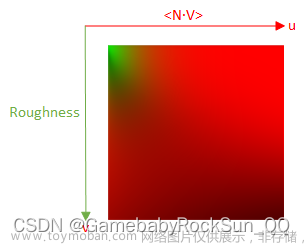
上图中已经标识清楚了纹理坐标轴的含义,需要注意的是,这与通常在 OpenGL 资料中看到的图上下是颠倒的,因为 D3D 的纹理坐标和 OpenGL 的纹理坐标是上下颠倒的。当然这也验证我们用D3D生成出来的LUT图是正确的。
在本章示例代码 Shader 文件GRSD3D12Sample/GRS_IBL_BRDF_Integration_LUT.hlsl 中最终实现的生成方法如下:
float2 IntegrateBRDF(float NdotV, float roughness)
{
float3 V;
V.x = sqrt(1.0f - NdotV * NdotV);
V.y = 0.0f;
V.z = NdotV;
float A = 0.0f;
float B = 0.0f;
float3 N = float3(0.0f, 0.0f, 1.0f);
uint SAMPLE_COUNT = GRS_INT_SAMPLES_CNT;
for (uint i = 0; i < SAMPLE_COUNT; ++i)
{
float2 Xi = Hammersley(i, SAMPLE_COUNT);
float3 H = ImportanceSampleGGX(Xi, N, roughness);
float3 L = normalize(2.0 * dot(V, H) * H - V);
float NdotL = max(L.z, 0.0); // N = (0.0f, 0.0f, 1.0f);
float NdotH = max(H.z, 0.0); // N = (0.0f, 0.0f, 1.0f);
float VdotH = max(dot(V, H), 0.0);
if ( NdotL > 0.0 )
{
float G = GeometrySmith_IBL(N, V, L, roughness);
float G_Vis = (G * VdotH) / (NdotH * NdotV);
float Fc = pow(1.0 - VdotH, 5.0);
A += (1.0 - Fc) * G_Vis;
B += Fc * G_Vis;
}
}
A /= float(SAMPLE_COUNT);
B /= float(SAMPLE_COUNT);
return float2(A, B);
}
float2 PSMain(ST_GRS_HLSL_VS_OUT pin) :SV_TARGET
{
return IntegrateBRDF(pin.m_v2UV.x, pin.m_v2UV.y);
}
代码思路已经很清晰了,就是按照我们之前拆分简化后的 BRDF 的蒙特卡洛积分形式进行编码。这段代码中需要注意的就是对于视见向量 V 的处理,其实使用了一个技巧即:
float3 V;
V.x = sqrt(1.0f - NdotV * NdotV);
V.y = 0.0f;
V.z = NdotV;
可以看出随着 n ⃗ ⋅ ω ⃗ o \vec{n} \cdot \vec{\omega}_o n⋅ωo 的值从 0 变化到 1,V的方向也从 X轴 方向旋转到了 Z轴方向,因为我们之前就假设 ω ⃗ o = n ⃗ \vec{\omega}_o = \vec{n} ωo=n ,所以这个旋转变化的技巧保证了视见向量是逐步在一个平面内旋转靠近法向量的,最终我们也按照假设认为法向量 N就是Z轴。
接着代码中依然使用了 Hammersley 版本的均匀分布随机数发生算法来生成随机数。并且使用了和预积分过滤贴图同样的重要性采样函数 ImportanceSampleGGX ,生成了指定概率分布的随机向量 h ⃗ \vec{h} h 。与镜面反射预积分过滤贴图一样,代码中依旧使用了 NdotL 来判断计算出的入射光线是否位于半球平面的正面,使用的方法也是一样的,就不在赘述了。
最后在 PSMain函数中直接使用纹理的 u,v 坐标作为参数计算了LUT 贴图上每一点的 BRDF 预积分值。
3.6、最终光照合成
至此,整个基于微表面理论的“Cook-Torrance” 模型的蒙特卡洛积分重要性采样的分析和预计算就完成了,最后在实际的实时渲染循环中,使用前面的预积分纹理并使用合适的 PBR材质参数进行采样合成计算即可得到物体在场景中的 PBR 光照渲染结果。
在本章示例的 Shader 文件 GRSD3D12Sample/GRS_PBR_IBL_PS_Without_Texture.hlsl 中的 PSMain 函数中合成光照实现代码如下(注意文件名中的 Without Texture是说没有使用PBR的材质纹理,而不是说不使用 IBL 的预积分贴图):
SamplerState g_sapLinear : register(s0);
TextureCube g_texSpecularCubemap : register(t0);
TextureCube g_texDiffuseCubemap : register(t1);
Texture2D g_texLut : register(t2);
struct ST_GRS_HLSL_PBR_PS_INPUT
{
float4 m_v4HPos : SV_POSITION;
float4 m_v4WPos : POSITION;
float4 m_v4WNormal : NORMAL;
float2 m_v2UV : TEXCOORD;
float4x4 m_mxModel2World : WORLD;
float3 m_v3Albedo : COLOR0; // 反射率
float m_fMetallic : COLOR1; // 金属度
float m_fRoughness : COLOR2; // 粗糙度
float m_fAO : COLOR3; // 环境遮挡因子
};
float4 PSMain(ST_GRS_HLSL_PBR_PS_INPUT stPSInput): SV_TARGET
{
float3 N = stPSInput.m_v4WNormal.xyz;
float3 V = normalize(g_v4EyePos.xyz - stPSInput.m_v4WPos.xyz);
float3 R = reflect(-V, N);
float3 F0 = float3(0.04f, 0.04f, 0.04f);
F0 = lerp(F0, stPSInput.m_v3Albedo, stPSInput.m_fMetallic);
float3 Lo = float3(0.0f,0.0f,0.0f);
// .......省略点光源直接光照计算部分
// 接着开始利用前面的预积分结果计算IBL光照的效果
// IBL漫反射环境光部分
float3 F = FresnelSchlickRoughness(max(dot(N, V), 0.0), F0, stPSInput.m_fRoughness);
float3 kS = F;
float3 kD = 1.0 - kS;
kD *= 1.0 - stPSInput.m_fMetallic;
// 采样漫反射辐照度贴图
float3 irradiance = g_texDiffuseCubemap.Sample(g_sapLinear, N).rgb;
// 与物体表面点P的颜色值相乘
float3 diffuse = irradiance * stPSInput.m_v3Albedo;
// IBL镜面反射环境光部分
const float MAX_REFLECTION_LOD = 5.0; // 与镜面反射预积分贴图的 Max Map Level 保持一致
// 采样镜面反射预积分辐照度贴图
float3 prefilteredColor = g_texSpecularCubemap.SampleLevel(g_sapLinear, R, stPSInput.m_fRoughness * MAX_REFLECTION_LOD).rgb;
// 采样 BRDF 预积分贴图
float2 brdf = g_texLut.Sample(g_sapLinear, float2(max(dot(N, V), 0.0), stPSInput.m_fRoughness)).rg;
// 合成计算镜面反射光辐射度,注意使用的是 F0 参数,与公式保持一致
float3 specular = prefilteredColor * (F0 * brdf.x + brdf.y);
// IBL 光照合成,注意用 kD 参数再衰减下漫反射成分,与最开初的渲染方程中保持一致
// m_fA0 是环境遮挡因子,目前总是设置其为 1
float3 ambient = (kD * diffuse + specular) * stPSInput.m_fAO;
// 直接光照 + IBL光照
float3 color = ambient + Lo;
// Gamma
//return float4(color, 1.0f);
return float4(LinearToSRGB(color),1.0f);
}
首先代码中直接使用点坐标的xyz分量当做了点 p ⃗ \vec{p} p 处的法线 N,这样就与我们在做几个预积分贴图时假设法线方向总是点 p ⃗ \vec{p} p 处的”正上方“相一致了。
其次代码中直接使用视见向量 V 的关于法线 N 的负反射向量 R 作为理想的入射光主方向来采样预积分辐照度贴图。这与我们在基本的几何光学中的反射定理是一致的。
最后漫反射光和镜面反射光都计算完毕后,就按照反射方程(渲染方程)一步步合成计算出了最终的光照颜色值。整个过程是比较清晰的了,就不在赘述了。
这里提醒大家注意的地方是,请注意:
// 合成计算镜面反射光辐射度,注意使用的是 F0 参数,与公式保持一致
float3 specular = prefilteredColor * (F0 * brdf.x + brdf.y);
这里应该使用原始的菲涅尔系数 F0 来计算镜面反射的效果,而不是使用已经用 F S c h l i c k F_{Schlick} FSchlick 函数计算后的 F 值,否则计算结果就是错误的。这个错误最先见于教程 [镜面IBL - LearnOpenGL CN (learnopengl-cn.github.io)](https://learnopengl-cn.github.io/07 PBR/03 IBL/02 Specular IBL/) 的代码中。在 UE 引擎中使用的也是 F0 值,当然需要进行金属度修正。
另外从整个合成光照的过程中可以看出,整个 PBR 渲染过程中,唯一受物体表面自身颜色影响的地方就是漫反射光分量,而且这个分量按照“金属工作流”的处理还会被进一步衰减,看似好像物体自身表面颜色不是很重要了。其实不然,这正是我们观察现实世界中各种物体表面真实反射效果后的很好的模拟,因为越接近金属材质的光滑表面,越是会反射环境光的部分,最终看上去实际很像一面镜子,而不会反映出其自身真实的颜色,但是会反应出其菲涅尔系数 F0 的效果。所以最终金属表面的颜色主要受菲涅尔系数 F0 的影响,而非金属表面的颜色就主要受其自身漫反射颜色的影响。
这一点从光照过程本身的原理上也很好理解,因为我们知道所谓镜面反射光,更多的时候就像是光直接被从物体表面反弹出来一样,所以受物体表面影响就很小,基本会保持光源的能量属性,也就是颜色属性。而漫反射光则是可能被物体表面吸收或不断的透射折射然后再折回物体表面发射出来的光线,其过程必然与物体表面甚至表面以下发生了复杂的交互作用,甚至有光子被电子吸收再释放的过程,所以漫反射光就像被物体表面“污染”了一样,带有更多的物体表面的颜色属性,而本身光源的颜色属性就非常弱了。
4、总结
至此总算在历时将近一个月之后,我将这篇教程全部编写整理完毕了,期间翻阅了很多资料,查证了很多公式,通过推演梳理整个IBL渲染过程中的数学原理,终于将整个 IBL过程搞清楚也能讲清楚了。
其实 PBR 中的有些理论最早都可以追溯到上个世纪的60年代,整个过程中有很多知名的不知名的大咖们奉献了很多方法和理论,而实时 PBR 更是迟到 2012 年因迪士尼的几篇论文而兴起,再经过 Epic 中众多大佬的打磨提炼,直至今天,实时 PBR 的应用才是方兴未艾之时。古语云:为天地立心、为生民立命、为往圣继绝学,为万世开太平!笔者整理这篇文章廖算做为先贤们继绝学吧。
最终 PBR IBL 的数学原理搞懂了,代码其实一下子就简单了,基本都是公式的直译,并不需要太多的编程技巧。而反之,我更加赞叹于在 PBR IBL 整个数学计算推导过程中,由 Epic 公司在 UE 引擎的具体实现中使用的大量数学技巧,感叹于自己之前的那点可怜的数学基础,至今也还只能停留在看懂整个过程的水平上。往后还是要加强数学方面的深入学习,尤其是应用方面要积累更多的经验,期盼早日能够完成从必然王国到自由王国的跃迁。文章来源:https://www.toymoban.com/news/detail-402062.html
当然这些数学技巧最终的目的都是在渲染质量和效率之间做了个折中,并且很多的近似和折中处理甚至都导致重要性采样本身已经失去了意义,也就是变成了所谓有偏的估计,尤其是最后为了能实现几个积分项的预计算,甚至使用了一些不严格的计算过程。这些方法虽然在数学上是很不严谨的,但在实际计算上,以及最终令人惊艳的渲染效果上,这点问题已经算不上什么了。正如我们反复强调的图形学第一定律所说,如果他看上去是正确的,那么他就是正确的!文章来源地址https://www.toymoban.com/news/detail-402062.html
5、参考资料
- 蒙特卡罗方法详解 - 知乎 (zhihu.com)
- 深入理解微表面模型 - 知乎 (zhihu.com)
- [理论 - LearnOpenGL CN (learnopengl-cn.github.io)](https://learnopengl-cn.github.io/07 PBR/01 Theory/)
- [光照 - LearnOpenGL CN (learnopengl-cn.github.io)](https://learnopengl-cn.github.io/07 PBR/02 Lighting/)
- [漫反射辐照 - LearnOpenGL CN (learnopengl-cn.github.io)](https://learnopengl-cn.github.io/07 PBR/03 IBL/01 Diffuse irradiance/)
- [镜面IBL - LearnOpenGL CN (learnopengl-cn.github.io)](https://learnopengl-cn.github.io/07 PBR/03 IBL/02 Specular IBL/)
到了这里,关于DirectX12(D3D12)基础教程(二十一)—— PBR:IBL 的数学原理(5/5)镜面反射积分项2及光照合成的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!










