线段树的学习(2023.4.5)-Toy模板网

这篇具有很好参考价值的文章主要介绍了线段树的学习(2023.4.5)。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

今天我来学习线段树

首先它是树有着'树'的结构,线段树由于本身是专门用来处理区间问题的

它的作用可以处理区间的问题拥有更快的速度.

对于每一个子节点而言，都表示整个序列中的一段子区间；对于每个叶子节点而言，都表示序列中的单个元素信息；子节点不断向自己的父亲节点传递信息，而父节点存储的信息则是他的每一个子节点信息的整合(信息的整合可能是求和,也可能是最大值,也可能是最小值)。

就是一个分块的思想.

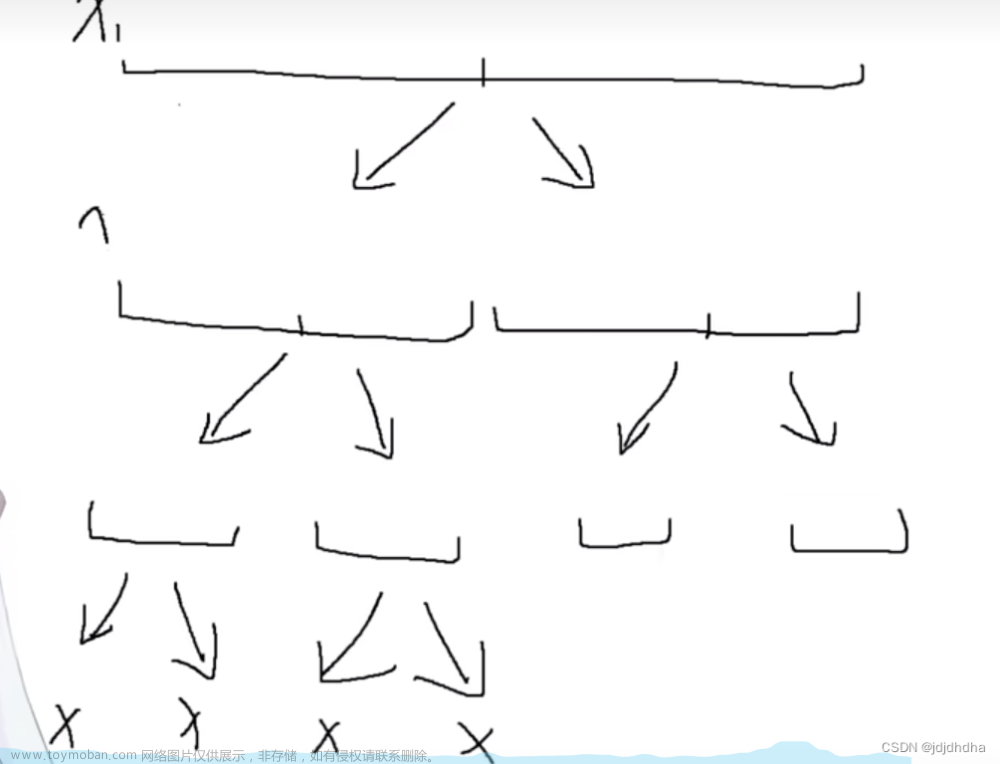
线段树的学习(2023.4.5)

一个大的区间不断的被二分找到区间的长度为1,

如上图每一个区间就是一个节点.

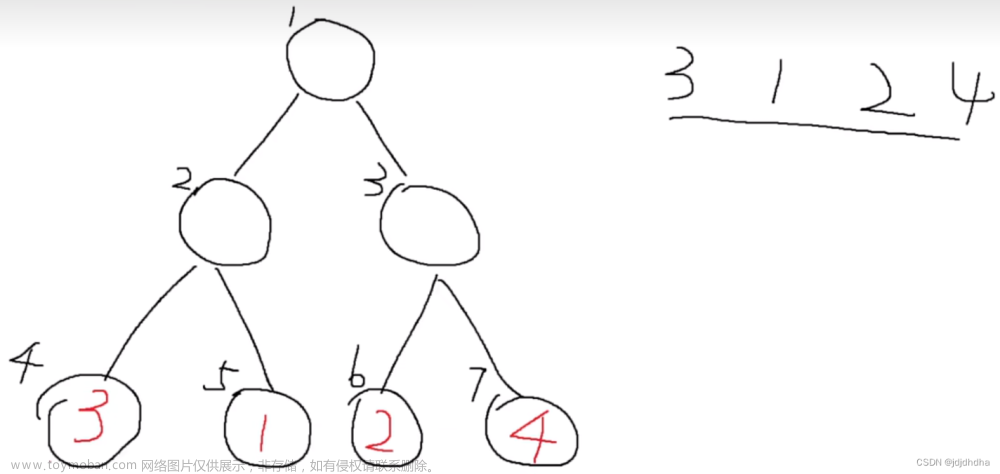
线段树的学习(2023.4.5)

数组3 1 2 4 就如上图一般

1节点代表区间1到4

2为1到2 3表示3到4

由于线段树满足完全二叉树,

节点x的左子节点为2x

右子节点为2x+1

用数组非长好的就可以实现.

以下的代码我一求区间的和为样例,用数组来模拟树的节点

int lchid(int x){//找左兒子
return 2*x;}

int rchid(int x){//找右兒子
return 2*x+1;}

这两函数就是直接找到你的二子的下标的. (其实也可以不写的,但是有的话调用就好了完全不用想).

这里选定的是求和的关系

tree数组的树的节点

void sum(int p){//向上维护(求和)
tree[p]=tree[lchid(p)]+tree[rchid(p)];
}

然后就是建树

p是当前节点的下标,l和r是p节点的区间标

void build(int p,int l,int r){
if(r==l){
    tree[p]=a[l];
    return ;
}
int mid=(l+r)/2;
build(lchid(p),l,mid);//向左边的区间递归
build(rchid(p),mid+1,r);//向右区间进行递归
sum(p);//对当前的节点进行维护(赋值);
}
//区间建树

到了区间长度为一的节点就赋值(给叶子节点赋值)

用到是是递归,一直递归下去要是出现赋值的数目超过了比如区间为3但是会有4个叶子节点

直接赋值为0即可

有时我们要修改某个区间的值

void updata(int ll,int rr,int l,int r,int p,int k){
//ll,rr是要修改的区间
//l,r是当前节点的区间p是当前节点的编号
//k是要修改的值(可能是加,也可能是减)

if(ll<=l&&rr>=r){//修改的区间完全包含当前区间
  lazyr(l,r,p,k);
        return ;
}
donm(p,l,r);
//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) updata(ll,rr,l,mid,lchid(p),k);

if(rr>mid) updata(ll,rr,mid+1,r,rchid(p),k);

sum(p);//对当前的节点要更新的

}
//区间修改

void lazyr(int l,int r,int p,int k){//改变区间的和,并打上lazy标记
lazy[p]+=k;
tree[p]+=k*(r-l+1);
}

void donm(int p,int l,int r){//k就是p节点的lazy值,向下传递lazy值
    int mid=(l+r)/2;
    lazyr(l,mid,lchid(p),lazy[p]);
    lazyr(mid+1,r,rchid(p),lazy[p]);
    lazy[p]=0;//把lazy向下传递后自己的lazy清空

}

你会问为啥要这样写

1,线段树在对区间处理时是用当前的区间与要处理的区间的包含关系来处理的

2类情况

1操作的区间包含当前的区间,就直接返回当前节点的区间值

2只有左或者右区间的端点包含,那就递归下去知道包含为止

2.为何要用到lazy数组以及donm函数

注意重点来了!

如果我们要对区间的值进行修改,非要递归到区间长度为一的时候进行修改,那线段树比起简单的数组处理区间就完全没有优势了,复杂度还会略高一点

所以就有了,每个节点的lazy值

lazy值就是要改的区间与包含当前的区间

那就不用继续往下更新了,直接把此节点的区间的值改了并且给一个lazy值表示这个节点,的子节点还未更新,要更新的值就是p的lazy值

我们不更新下面的值那下面的值不是错了吗?

当然有方法的,下次当我们要递归到本节点的子节点是

要判断当前的节点的lazy值(>0就是存在)

那就更新两个子节点的值即可,也不用再往下了.

这样就不会一修改就直接到叶子节点了

要用到了再修改

思想就是延迟更新

区间求和

ll find(int ll,int rr,int l,int r,int p){
    if(ll<=l&&rr>=r){//修改的区间完全包含当前区间
            ans+=tree[p];
        return 0;
    }
donm(p,l,r);

//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) find(ll,rr,l,mid,lchid(p));

if(rr>mid) find(ll,rr,mid+1,r,rchid(p));

return ans;
}

依旧是递归遍历

要是要用到子节点就以lazy判断要不要更新(我没判断,lazy=0,在函数中不会对数据有改变,但是判断了运行速度会快一点点)

ok讲了这摩多

来个板子吧!

复制Markdown 展开

题目描述

如题，已知一个数列，你需要进行下面两种操作：

将某区间每一个数加上 �k。
求出某区间每一个数的和。

输入格式

第一行包含两个整数 �,�n,m，分别表示该数列数字的个数和操作的总个数。

第二行包含 �n 个用空格分隔的整数，其中第 �i 个数字表示数列第 �i 项的初始值。

接下来 �m 行每行包含 33 或 44 个整数，表示一个操作，具体如下：

1 x y k：将区间 [�,�][x,y] 内每个数加上 �k。
2 x y：输出区间 [�,�][x,y] 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

输入输出样例

输入 #1复制

输出 #1复制

11
8
20

说明/提示

对于 30%30% 的数据：�≤8n≤8，�≤10m≤10。
对于 70%70% 的数据：�≤103n≤103，�≤104m≤104。
对于 100%100% 的数据：1≤�,�≤1051≤n,m≤105。

保证任意时刻数列中所有元素的绝对值之和 ≤1018≤1018。

【样例解释】

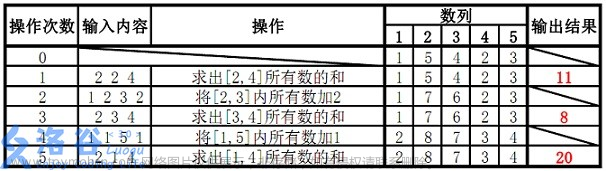
线段树的学习(2023.4.5)

出自洛谷:p3372

#include<stdio.h>
#define maxsize 100000
typedef long long ll;//long long 麻烦好长的就用ll
ll tree[maxsize*4];//用數字模擬樹
int lazy[maxsize*4]={0};//lazy數組
int a[100050];
ll ans=0;

int lchid(int x){//找左兒子
return 2*x;}

int rchid(int x){//找右兒子
return 2*x+1;}

void sum(int p){//向上维护(求和)
tree[p]=tree[lchid(p)]+tree[rchid(p)];
}

void lazyr(int l,int r,int p,int k){//改变区间的和,并打上lazy标记
lazy[p]+=k;
tree[p]+=k*(r-l+1);
}

void donm(int p,int l,int r){//k就是p节点的lazy值,向下传递lazy值
    int mid=(l+r)/2;
    lazyr(l,mid,lchid(p),lazy[p]);
    lazyr(mid+1,r,rchid(p),lazy[p]);
    lazy[p]=0;//把lazy向下传递后自己的lazy清空

}
//lazy下传的函数

void build(int p,int l,int r){
if(r==l){
    tree[p]=a[l];
    return ;
}
int mid=(l+r)/2;
build(lchid(p),l,mid);//向左边的区间递归
build(rchid(p),mid+1,r);//向右区间进行递归
sum(p);//对当前的节点进行维护(赋值);
}
//区间建树

void updata(int ll,int rr,int l,int r,int p,int k){
//ll,rr是要修改的区间
//l,r是当前节点的区间p是当前节点的编号
//k是要修改的值(可能是加,也可能是减)

if(ll<=l&&rr>=r){//修改的区间完全包含当前区间
  lazyr(l,r,p,k);
        return ;
}
donm(p,l,r);
//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) updata(ll,rr,l,mid,lchid(p),k);

if(rr>mid) updata(ll,rr,mid+1,r,rchid(p),k);

sum(p);//对当前的节点要更新的

}
//区间修改

ll find(int ll,int rr,int l,int r,int p){
    if(ll<=l&&rr>=r){//修改的区间完全包含当前区间
            ans+=tree[p];
        return 0;
    }
donm(p,l,r);

//要是当前的区间没有匹配的话就要对下面的节点进行更新了
int mid=(r+l)/2;
if(ll<=mid) find(ll,rr,l,mid,lchid(p));

if(rr>mid) find(ll,rr,mid+1,r,rchid(p));

return ans;
}
//区间求和

int main(){

int n,m;
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);

build(1,1,n);//起始点为1,区间为1到n的建树
while(m--){
    int q,w,e,r;
    scanf("%d",&q);
    if(q==1){
        scanf("%d%d%d",&w,&e,&r);
        updata(w,e,1,n,1,r);
    }
    else{
           ans=0;
        scanf("%d%d",&w,&e);

        printf("%lld\n",find(w,e,1,n,1));
    }
}
return 0;
}

没得解释,就是板子题,算法的每一行都有我的理解和注释

该算法刚学不熟悉,看着大佬的题解来的

每一行都尽量的去理解

这就是我的忍道!

ok 撒花谢幕!!!!!文章来源地址https://www.toymoban.com/news/detail-411318.html

到了这里，关于线段树的学习(2023.4.5)的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！