一、什么是字典树?
Trie 树,也叫“字典树”。顾名思义,它是一个树形结构。它是一种专门处理字符串匹配的数据结构,用来解决在一组字符串集合中快速查找某个字符串的问题。
Trie 树的本质,就是利用字符串之间的公共前缀,将重复的前缀合并在一起。
举个例子,现在我们要存储一些字符串。
1️⃣ 只要前缀相同的我们就不需要两个节点来存储,但是要注意ABCD和ATCD这两个字符串从B和T就分开了,所以后面的CD就不会存到一起。
2️⃣ 有可能一个字符串是另一个字符串的前缀。所以我们需要一个变量来标志一个字符串的结尾,也能标识有多少个这个字符串。
二、字典树的相关操作
2.1 插入
const int N = 1e6 + 10;
int son[N][26];// 记录下一个节点在第几层
int cnt[N];// 标识字符串结尾
int idx;// 记录下一个要存节点的层数
son数组的作用是记录储存子节点的位置,而26则代表了26个字符,类似于26叉树。
而cnt的作用就是标志一个字符串的结尾,顺便记录有多少个该字符串。idx表示当前要插入的节点(新建节点)。
void insert(const string& s)
{
int p = 0;// 从根开始找,如果没有说明需要新的根
for(int i = 0; i < s.size(); i++)
{
int u = s[i] - 'a';
if(!son[p][u])// 没有就创建
{
son[p][u] = ++idx;
}
p = son[p][u];
}
cnt[p]++;
}
用一张图理解一下,假设现在要插入"ac"和"bc":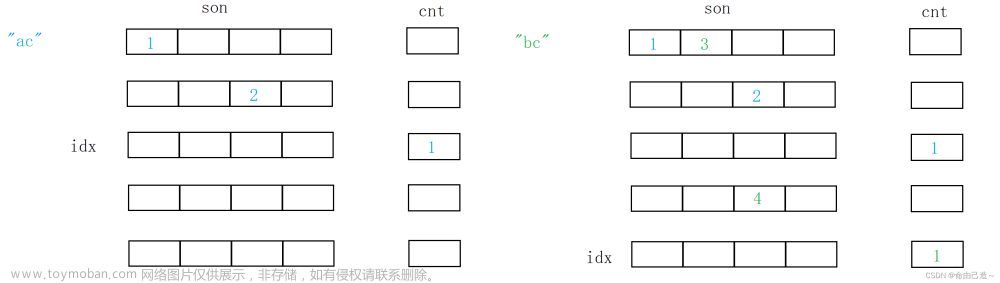
这也说明了不管是插入还是查找,第一个字符都是在第0层,所以初始化p = 0。
2.2 查找
查找的操作就类似于插入,如果不存在直接返回0即可。
int search(const string& s)
{
int p = 0;
for(int i = 0; i < s.size(); i++)
{
int u = s[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
2.3 例题:Trie字符串统计
题目链接
题目描述
维护一个字符串集合,支持两种操作:
I x向集合中插入一个字符串 x;Q x询问一个字符串在集合中出现了多少次。
共有 N个操作,所有输入的字符串总长度不超过 1e5,字符串仅包含小写英文字母。
输入格式
第一行包含整数 N,表示操作数。接下来 N行,每行包含一个操作指令,指令为 I x 或 Q x 中的一种。
输出格式
对于每个询问指令 Q x,都要输出一个整数作为结果,表示 x在集合中出现的次数。
每个结果占一行。
数据范围
1≤N≤2∗1e4
输入样例:
5
I abc
Q abc
Q ab
I ab
Q ab
输出样例:
1
0
1
#include <iostream>
#include <string>
using namespace std;
const int N = 1e6 + 10;
int son[N][26];// 记录下一个节点在第几层
int cnt[N];// 标识字符串结尾
int idx;// 记录下一个要存节点的层数
void insert(const string& s)
{
int p = 0;// 从根开始找,如果没有说明需要新的根
for(int i = 0; i < s.size(); i++)
{
int u = s[i] - 'a';
if(!son[p][u])// 没有就创建
{
son[p][u] = ++idx;
}
p = son[p][u];
}
cnt[p]++;
}
int search(const string& s)
{
int p = 0;
for(int i = 0; i < s.size(); i++)
{
int u = s[i] - 'a';
if(!son[p][u]) return 0;
p = son[p][u];
}
return cnt[p];
}
int main()
{
int n;
cin >> n;
string s1, s2;
while(n--)
{
cin >> s1 >> s2;
if(s1 == "I")
{
insert(s2);
}
else
{
cout << search(s2) << endl;
}
}
return 0;
}
三、应用:最大异或对
题目链接
题目描述
在给定的 N个整数 A1,A2……AN中选出两个进行 xor(异或)运算,得到的结果最大是多少?
输入格式
第一行输入一个整数 N。第二行输入 N个整数 A1~AN。
输出格式
输出一个整数表示答案。
数据范围
1≤N≤105, 0≤Ai<231
输入样例:
3
1 2 3
输出样例:
3
思路分析:
首先我们要知道什么时候两个数字异或值最大?
答案是当两个数的二进制位每一位都不相同的时候最大。
我们知道一个数有32个比特位,最高位不用管(符号位),所以我们就要看第0 ~ 30位。
因为比特位有原子性(只有两态),我们可以分两种情况:一种是比特位相同,一种是不同,而为了保证最大,从最高位开始,如果两种情况的话每次尽量往不同的方向走,只有一种情况就没有办法。我们边查找边统计总和,走到最后即可得到异或的值,所以我们边查找就能边统计最大的异或对。
#include <iostream>
using namespace std;
const int N = (1e5 + 10) * 31;
int son[N][2], idx;
void insert(int x)
{
int p = 0;
for(int i = 30; i >= 0; i--)
{
int u = (x >> i) & 1;
if(!son[p][u]) son[p][u] = ++idx;
p = son[p][u];
}
}
int search(int x)
{
int p = 0, res = 0;
for(int i = 30; i >= 0; i--)
{
int u = (x >> i) & 1;
// 尽量往不在的那一边走
// 另一边存在就异或
if(son[p][!u])
{
res = res * 2 + 1;
p = son[p][!u];
}
else
{
res = res * 2;
p = son[p][u];
}
}
return res;
}
int main()
{
int n;
cin >> n;
int res = 0;
while(n--)
{
int x;
cin >> x;
insert(x);
int tmp = search(x);
res = max(res, tmp);
}
cout << res << endl;
return 0;
}
四、总结
我们上面的题目也可以使用哈希来解决,但是trie树在某些方面它的用途更大,比如说对于某一个单词,我们要询问它的前缀是否出现过。这样hash就不好搞了,而用trie还是很简单。
上面我们使用数组模拟出来的,当然也可以用链式结构:文章来源:https://www.toymoban.com/news/detail-416120.html
#define MAX 26
typedef struct trie {
struct trie* node[MAX];
int v;
} Trie;
用一道leetcode的例题举例:
题目链接
代码:文章来源地址https://www.toymoban.com/news/detail-416120.html
class Trie {
public:
vector<Trie*> son;
bool flag;
Trie* searchend(string s)
{
Trie* node = this;
for(int i = 0; i < s.size(); i++)
{
int u = s[i] - 'a';
if(!node->son[u])
{
return nullptr;
}
node = node->son[u];
}
return node;
}
Trie()
: son(26)
, flag(false)
{}
void insert(string word) {
Trie* node = this;
for(int i = 0; i < word.size(); i++)
{
int u = word[i] - 'a';
if(!node->son[u])
{
node->son[u] = new Trie;
}
node = node->son[u];
}
node->flag = true;
}
bool search(string word) {
Trie* node = searchend(word);
if(node && node->flag)
{
return true;
}
return false;
}
bool startsWith(string prefix) {
Trie* node = searchend(prefix);
if(node)
{
return true;
}
return false;
}
};
/**
* Your Trie object will be instantiated and called as such:
* Trie* obj = new Trie();
* obj->insert(word);
* bool param_2 = obj->search(word);
* bool param_3 = obj->startsWith(prefix);
*/
到了这里,关于【数据结构与算法】深刨Trie树(字典树)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!













