赫夫曼编码树（图解+完整代码）

这篇具有很好参考价值的文章主要介绍了赫夫曼编码树（图解+完整代码）。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

在我学习离散数学的时候，就已经接触了赫夫曼树与赫夫曼编码，于是在数据结构的课程中，竟然直接跳过了！但我仍记得构造赫夫曼树，是当时离散数学期末考试的12分大题，足以见其重要性！那这次不仅要把其构造算法讲清楚，还要把代码给理清楚。

⚽1.相关概念

🏐2.赫夫曼树

🏀3.赫夫曼编码

🥎4.完整代码

4.1存储结构

4.2创建赫夫曼树

4.3创建赫夫曼编码

4.4完整代码

⚽1.相关概念

在介绍赫夫曼树之前，我们先介绍4个相关概念，帮助我们更好的来定义哈夫曼树

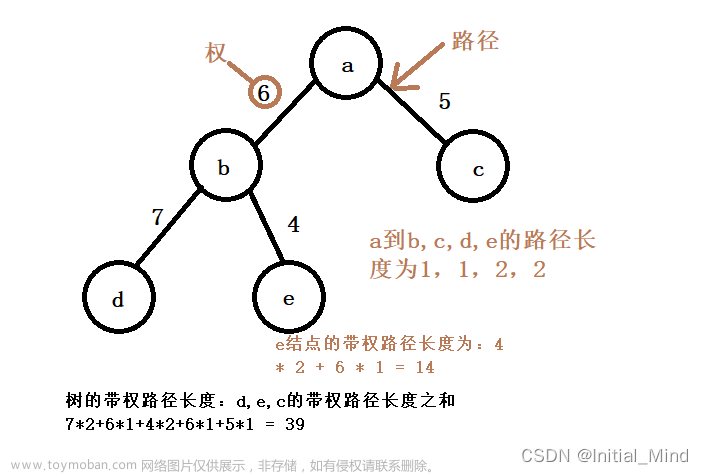
结点的路径长度：从根结点到该结点的路径上分支的数目

树的路径长度：树中每个结点的路径长度之和

结点的带权路径长度：从根结点到该结点的路径长度与结点上权的乘积

树的带权路径长度：树中所有叶子结点的带权路径长度之和

🏐2.赫夫曼树

定义：在所有含 n 个叶子结点、并且叶子结点带相同权值的二叉树中，其带权路径长度WPL最小的那棵二叉树称为赫夫曼树，也叫最优二叉树。

那如何构造赫夫曼树呢？

输入：n 和n 个权值 {w1 , w2 , …, wn }

输出：赫夫曼树

步骤：

根据给定的 n 个权值 {w1 , w2 , …, wn }，构造 n 棵二叉树的集合 F = {T1 , T2 , … , Tn }，其中每棵二叉树中均只含一个带权值为 wi 的根结点，其左、右子树为空树

在F 中选取其根结点的权值为最小和次小的两棵二叉树，分别作为左、右子树构造一棵新的二叉树，并置这棵新的二叉树根结点的权值为其左、右子树根结点的权值之和

从F中删去这两棵树，同时加入刚生成的新树

重复 2 和 3 两步，直至 F 中只含一棵树为止

我们以例子说明，输入：已知n=5，权值集合 W={ 5, 6, 2, 9, 7 }。

赫夫曼编码树（图解+完整代码）

就这样，一棵赫夫曼树就构建好了，我们可以发现：

赫夫曼算法采用的是贪心策略，贪心策略不是对所有问题都能得到最优解，但赫夫曼算法得到的是最优解

n个叶子结点的赫夫曼树共有2n-1个结点

赫夫曼树中不会有度为1的结点

此时，有同学就要问了，哈夫曼树有啥用呢？别着急，下面接着讲。

🏀3.赫夫曼编码

背景：在数据膨胀、信息爆炸的今天，数据压缩的意义不言而喻。谈到数据压缩，就不能不提赫夫曼（Huffman）编码，赫夫曼编码是首个实用的压缩编码放案，即使在今天的许多知名压缩算法里，依然可以见到赫夫曼编码的影子。

另外，在数据通信中，用⼆进制给每个字符进行编码时不得不面对的⼀个问题是如何使电文总长最短且不产生二义性。根据字符出现频率，利用赫夫曼编码可以构造出⼀种不等长的二进制，使编码后的电文长度最短，且保证不产生二义性。

同样，我们先介绍几个相关概念

定长编码：

ASCII编码、Unicode编码：ASCII编码每⼀个字符使用8个bit，能够编码256个字符；Unicode 编码每个字符占16个bit，能够编码65536个字符，包含所有ASCII编码的字符。

假设我们要使用定长编码对由符号A，B，C，D和E构造的消息进行编码，对每个字符编码需要多少位呢？至少需要3位，2个bit位不够表示五个字符，只能表示4个字符。

如果对DEAACAAAAABA进⾏编码呢？总共12个字符，每个字符需要3bit，总共需要36位

而定长编码有一定的缺陷：浪费空间。我们希望出现频率高的字符编码短一些，出现频率低的字符编码长一些，这样就可以尽可能使用较少的空间就传递了同样的信息，于是就产生了变长编码。

变长编码：

单个编码的长度不⼀样，可以根据整体出现的频率来调节，出现的频率越高，编码长度越短。

变长编码优于定长编码：变长编码可以将短编码赋予平均出现频率较高的字符，同⼀消息的编码长度小于定长编码。

这时，又产生了一个问题：字符有长有短，我们怎么知道⼀个字符从哪里开始，⼜从哪里结束呢？如果位数固定，就没这个问题了。

前缀属性：

字符集当中的⼀个字符编码不是其他字符编码的前缀，则这个字符编码具有前缀属性

所谓前缀，⼀个编码可以被解码为多个字符，表示不唯⼀

我们不妨来看个例子，我们随意对字符进行二进制编码：

字符	编码
P	000
Q	11
R	01
S	001
T	10

可以看出：以上编码都具有前缀属性，于是编码不会产生二义性。比如01001101100010 可以翻译为RSTQPT，不会翻译成其他的字符串。

而下面这个编码，就会产生歧义：10到底是S还是QP呢？显然，这种编码就不行。

字符	编码
P	0
Q	1
R	01
S	10
T	11

前缀码：所谓的前缀码，就是没有任何码字是其他码字的前缀。

铺垫了这么久，终于要讲到赫夫曼编码了：赫夫曼编码就是一种前缀码，在构造编码时，就是用一棵赫夫曼树来进行构造的。于是，我们可以称其为赫夫曼编码树。

它的方法是什么呢？我们直接上赫夫曼编码树的特征。

赫曼编码树是⼀颗二叉树

每片叶子结点都包含⼀个字符

从结点到其左孩子的路径上标记0

从结点到其右孩子的路径上标记1

从根结点到包含字符的叶⼦结点的路径上获得的叶结点的编码

编码均具有前缀属性

我们继续用上面构造的赫夫曼树来举例：

赫夫曼编码树（图解+完整代码）

显然，权重越大，即出现频率越高的字符，他们的编码相对更短；并且，他们都是前缀码，不会产生二义性。

🥎4.完整代码

上述过程都了解后，我们就可以开始想代码实现了。每个人的方法都不同，下面仅给出我的方法。

4.1存储结构

首先，我们应该思考用什么来存储赫夫曼树的结构。赫夫曼树是一棵二叉树，所以应该用二叉树的存储结构，包括顺序存储与链式存储。

深入剖析二叉树https://blog.csdn.net/weixin_54186646/article/details/124099967?spm=1001.2014.3001.5501由于赫夫曼树不会出现斜树的极端情况，故可用数组来存储。

/*哈夫曼树结构*/
//可以用数组连续存储，不会浪费空间
//故用数组下标存储左右孩子、父亲结点
typedef struct
{
	int weight;
	int left;
	int right;
	int parent;
}Node, * HuffmanTree;

4.2创建赫夫曼树

现在开始创建赫夫曼树。

叶子结点一共有n个，那总结点数为2n-1个

对前n个结点初始化，赋上权重，此时还没有父节点、孩子结点，均设为0；

对其他结点进行初始化，暂时都为0

挑选出无父节点的两最小结点

以这两个结点构建他们的父节点

不断循环，直到第2n-1个结点构建结束

void CreateHuffmanTree(HuffmanTree* T, int w[], int n)
{
	int m = 2 * n - 1;//n个叶子结点，共m个结点
	int m1, m2;//用于建立下一个结点的两结点，值为最小的两个
	*T = (HuffmanTree)malloc((m + 1) * sizeof(Node));
	//初始化前n个结点（叶子结点），权重赋值，暂时没有左右孩子与父亲
	for (int i = 1; i <= n; i++)
	{
		(*T)[i].weight = w[i];
		(*T)[i].left = 0;
		(*T)[i].right = 0;
		(*T)[i].parent = 0;
	}

	//初始化[n+1,m]个结点(非叶子结点)
	for (int i = n + 1; i <= m; i++)
	{
		(*T)[i].weight = 0;
		(*T)[i].left = 0;
		(*T)[i].right = 0;
		(*T)[i].parent = 0;
	}

	//开始建树，第i个结点的两孩子为m1,m2，权重为两孩子结点权重之和
	for (int i = n + 1; i <= m; i++)
	{
		select(T, i - 1, &m1, &m2);
		(*T)[i].left = m1;
		(*T)[i].right = m2;
		(*T)[m1].parent = i;
		(*T)[m2].parent = i;
		(*T)[i].weight = (*T)[m1].weight + (*T)[m2].weight;

		printf("%d (%d %d)\n", (*T)[i].weight, (*T)[m1].weight, (*T)[m2].weight);
	}
	printf("\n");
}

在上述代码中，出现了select函数，其作用就是筛选出无父节点的最小和此小结点。

/*选取得到n个无父节点的两最小结点*/
void select(HuffmanTree* T, int n, int* m1, int* m2)
{
	int m;//存储最小值的数组下标

	//给m赋初值
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0)
		{
			m = i;
			break;
		}
	}
	//找到当前最小的权重（叶子结点）
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && (*T)[i].weight < (*T)[m].weight)
		{
			m = i;
		}
	}
	//先赋给m1保存一个，再去寻找第二小的值
	*m1 = m;
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && i != *m1)
		{
			m = i;
			break;
		}
	}
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && i != *m1 && (*T)[i].weight < (*T)[m].weight)
		{
			m = i;
		}
	}
	//保存第二小的数
	*m2 = m;
}

4.3创建赫夫曼编码

/*创建哈夫曼编码*/
//从n个叶子结点到根节点逆向求解
void CreateHuffmanCode(HuffmanTree* T, HuffmanCode* C, int n)
{
	//编码长度为s-1,第s位为\0
	int s = n - 1;
	//当前结点的父节点数组下标
	int p = 0;
	//为哈夫曼编码分配空间
	C = (HuffmanCode*)malloc((n + 1) * sizeof(char*));
	//临时保存当前叶子结点的哈夫曼编码
	char* cd = (char*)malloc(n * sizeof(char));
	//最后一位为\0
	cd[n - 1] = '\0';

	for (int i = 1; i <= n; i++)
	{
		s = n - 1;
		//c指向当前结点,p指向此结点的父节点,两者交替上升，直到根节点
		for (int c = i, p = (*T)[i].parent; p != 0; c = p, p = (*T)[p].parent)
		{
			//判断此结点为父节点的左孩子还是右孩子
			if ((*T)[p].left == c)
				cd[--s] = '0';//左孩子就是编码0
			else
				cd[--s] = '1';//右孩子就是编码1
		}
		//为第i个编码分配空间
		C[i] = (char*)malloc((n - s) * sizeof(char));
		//将此编码赋值到整体编码中
		strcpy(C[i], &cd[s]);
	}
	//释放
	free(cd);
	//打印编码序列
	for (int i = 1; i <= n; i++)
	{
		printf("%d %s", (*T)[i].weight, C[i]);
		printf("\n");
	}
}

4.4完整代码

#include<stdlib.h>
#include<stdio.h>
/*哈夫曼树结构*/
//可以用数组连续存储，不会浪费空间
//故用数组下标存储左右孩子、父亲结点
typedef struct
{
	int weight;
	int left;
	int right;
	int parent;
}Node, * HuffmanTree;

//存储哈夫曼编码
typedef char* HuffmanCode;
void CreateHuffmanTree(HuffmanTree* T, int w[], int n);
void select(HuffmanTree* T, int n, int* m1, int* m2);
void CreateHuffmanCode(HuffmanTree* T, HuffmanCode* C, int n);
/*创建哈夫曼树*/
//传入n个权重，作为哈夫曼树的n个叶子结点
void CreateHuffmanTree(HuffmanTree* T, int w[], int n)
{
	int m = 2 * n - 1;//n个叶子结点，共m个结点
	int m1, m2;//用于建立下一个结点的两结点，值为最小的两个
	*T = (HuffmanTree)malloc((m + 1) * sizeof(Node));
	//初始化前n个结点（叶子结点），权重赋值，暂时没有左右孩子与父亲
	for (int i = 1; i <= n; i++)
	{
		(*T)[i].weight = w[i];
		(*T)[i].left = 0;
		(*T)[i].right = 0;
		(*T)[i].parent = 0;
	}

	//初始化[n+1,m]个结点(非叶子结点)
	for (int i = n + 1; i <= m; i++)
	{
		(*T)[i].weight = 0;
		(*T)[i].left = 0;
		(*T)[i].right = 0;
		(*T)[i].parent = 0;
	}

	//开始建树，第i个结点的两孩子为m1,m2，权重为两孩子结点权重之和
	for (int i = n + 1; i <= m; i++)
	{
		select(T, i - 1, &m1, &m2);
		(*T)[i].left = m1;
		(*T)[i].right = m2;
		(*T)[m1].parent = i;
		(*T)[m2].parent = i;
		(*T)[i].weight = (*T)[m1].weight + (*T)[m2].weight;

		printf("%d (%d %d)\n", (*T)[i].weight, (*T)[m1].weight, (*T)[m2].weight);
	}
	printf("\n");
}

/*选取得到n个无父节点的两最小结点*/
void select(HuffmanTree* T, int n, int* m1, int* m2)
{
	int m;//存储最小值的数组下标

	//给m赋初值
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0)
		{
			m = i;
			break;
		}
	}
	//找到当前最小的权重（叶子结点）
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && (*T)[i].weight < (*T)[m].weight)
		{
			m = i;
		}
	}
	//先赋给m1保存一个，再去寻找第二小的值
	*m1 = m;
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && i != *m1)
		{
			m = i;
			break;
		}
	}
	for (int i = 1; i <= n; i++)
	{
		if ((*T)[i].parent == 0 && i != *m1 && (*T)[i].weight < (*T)[m].weight)
		{
			m = i;
		}
	}
	//保存第二小的数
	*m2 = m;
}

/*创建哈夫曼编码*/
//从n个叶子结点到根节点逆向求解
void CreateHuffmanCode(HuffmanTree* T, HuffmanCode* C, int n)
{
	//编码长度为s-1,第s位为\0
	int s = n - 1;
	//当前结点的父节点数组下标
	int p = 0;
	//为哈夫曼编码分配空间
	C = (HuffmanCode*)malloc((n + 1) * sizeof(char*));
	//临时保存当前叶子结点的哈夫曼编码
	char* cd = (char*)malloc(n * sizeof(char));
	//最后一位为\0
	cd[n - 1] = '\0';

	for (int i = 1; i <= n; i++)
	{
		s = n - 1;
		//c指向当前结点,p指向此结点的父节点,两者交替上升，直到根节点
		for (int c = i, p = (*T)[i].parent; p != 0; c = p, p = (*T)[p].parent)
		{
			//判断此结点为父节点的左孩子还是右孩子
			if ((*T)[p].left == c)
				cd[--s] = '0';//左孩子就是编码0
			else
				cd[--s] = '1';//右孩子就是编码1
		}
		//为第i个编码分配空间
		C[i] = (char*)malloc((n - s) * sizeof(char));
		//将此编码赋值到整体编码中
		strcpy(C[i], &cd[s]);
	}
	//释放
	free(cd);
	//打印编码序列
	for (int i = 1; i <= n; i++)
	{
		printf("%d %s", (*T)[i].weight, C[i]);
		printf("\n");
	}
}

int main()
{
	HuffmanTree T;
	HuffmanCode C;
	int n, w1, * w;
	scanf_s("%d", &n);
	w = (int*)malloc((n + 1) * sizeof(int));
	for (int i = 1; i <= n; i++)
	{
		scanf_s("%d", &w1);
		w[i] = w1;
	}
	printf("\n");
	CreateHuffmanTree(&T, w, n);
	CreateHuffmanCode(&T, &C, n);
	return 0;
}

我们来看看运行结果：