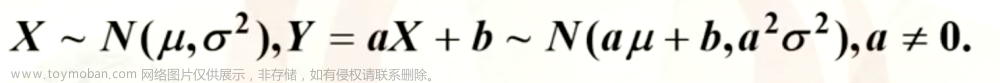正态分布t个标准差范围内的概率-Toy模板网

这篇具有很好参考价值的文章主要介绍了正态分布t个标准差范围内的概率。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

如果一个随机变量具有概率密度函数

$\begin{aligned} f(x)=\frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}, \quad -\infty < x < \infty \end{aligned}$

则称X为正态随机变量并记为 $\sim N(\mu, \sigma^2)$ ．这里N 为"Normal"
一词的首字母． $\mu, \sigma$ 都是常数， $\mu$ 为均值，可以取任何实数值,
而 $\sigma^2 < \infty$ 为方差， $\sigma$
称为标准差。这种分布我们称之为正态分布，德国数学家Gauss率先将其应用于天文学研究，故正态分布又叫高斯分布。

下面是 $\mu=1, \sigma=1$ 和 $\mu=1,\sigma=\frac{1}{2}$
的正态分布概率密度函数图像：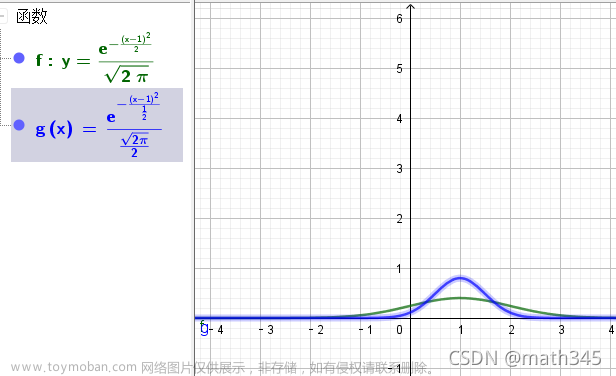
正态分布t个标准差范围内的概率

我们知道 $x=\mu$ 均值时，概率密度值最大，比如当标准差 $\sigma=1$
时的概率密度值为 $f(\mu) = \frac{1}{\sqrt{2\pi} \sigma} = 0.3989$

问题1： t个标准差范围内的概率 $P(u-t\sigma \le x \le u+t\sigma)$
是一个定值吗？和参数 $\sigma$ 有没有关系？其中 t 为大于0的实数。

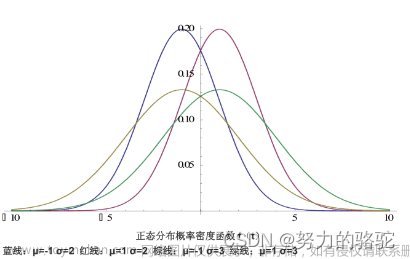
下图在很多关于概率的书本中都可以找到，它形象的展示了正态分布下，值离均值的距离为-1个标准差到1个标准差的概率约为68%(即曲线从-1到1围成的面积)，-2个标准差时概率约为95%，-3个标准差时概率约为99.7%
。但是大部分教材没有告诉我们为什么就是一个定值，这个值是怎么计算出来的？

正态分布t个标准差范围内的概率

其实我们做下下面的变换，就可以断定：不论是什么参数下的正态分布，t个标准差范围内的概率 $P(u-t\sigma \le x \le u+t\sigma)$ 都是一个定值，和参数 $\sigma$
无关，这真是一件神奇的事情。

$\begin{aligned} &P(u-t\sigma \le x \le u+t\sigma) \\ &= \int_{u-t\sigma}^{u+t\sigma} \frac{1}{\sqrt{2\pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}} dx \\ &= \frac{1}{\sqrt{2\pi} \sigma} \int_{u-t\sigma}^{u+t\sigma} e^{-(\frac{x-\mu}{\sqrt{2}\sigma})^2} dx \\ &=\frac{\sqrt{2}\sigma}{\sqrt{2\pi} \sigma} \int_{u-t\sigma}^{u+t\sigma} e^{-(\frac{x-\mu}{\sqrt{2}\sigma})^2} d\frac{x-\mu}{\sqrt{2}\sigma} \\ &=\frac{2}{\sqrt{\pi}} \int_{0}^{\frac{t}{\sqrt{2}}} e^{-y^2} d y \qquad (1) \end{aligned}$

问题2：如何计算(1)式？

如果我们直接去求不定积分 $\int e^{-x^2} dx$
的初等函数表达式，那我们就会掉进坑里。因为 $e^{-x^2}$ 这个函数的原函数不是初等函数！

为了解决上面的问题，这里先介绍下 $e^{-x^2-y^2}$ 函数的二重积分，转成极坐标的形式计算。下面面积D是一个半径 $\rho=a$ 的圆。

$\begin{aligned} \int\int_D e^{-x^2-y^2} dx dy &= \int_0^{2\pi} \int_0^a e^{-\rho^2} \rho d\rho d\theta \\ &= \int_0^{2\pi} -\frac{1}{2}e^{-\rho^2}\Big|_0^a d\theta \\ &= \int_0^{2\pi} -\frac{1}{2}(e^{-a^2} -1) d\theta \\ &= \frac{1}{2}(1-e^{-a^2})\theta \Big|_0^{2\pi}\\ &= \pi(1-e^{-a^2}) \qquad (2) \end{aligned}$

不难想象这个函数的图形，首先考虑一元函数 $e^{-x}$ 的图形，然后注意到
$-(x^2+y^2) \le 0$ , 即 $e^{-(x^2+y^2)}$ 的最大值为 $e^0=1$ , 其次 $x^2+y^2$
可以看成半径从 0 到 $+\infty$ 变化的圆, 半径越大 $e^{-(x^2+y^2)}$
越小，所以它的图像应该长下面的样子：

正态分布t个标准差范围内的概率

那么如何建立起 $\int_0^{+\infty} e^{-x^2} dx$ 和
$\int\int_D e^{-x^2-y^2} dx dy$ 的关系？不难想到
$\int_0^{+\infty} e^{-y^2} dy = \int_0^{+\infty} e^{-x^2} dx$

那么

$\begin{aligned} (\int_0^{+\infty} e^{-x^2} dx )^2 &= \int_0^{+\infty} e^{-x^2} dx \int_0^{+\infty} e^{-y^2} dy \\ &= \int_0^{+\infty} \int_0^{+\infty} e^{-x^2-y^2} dx dy \\ &= \frac{1}{4} \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} e^{-x^2-y^2} dx dy \\ &=\frac{1}{4}\lim_{a \to \infty} \pi(1-e^{-a^2}) \\ &=\frac{\pi}{4} \end{aligned}$

于是得到
$\int_0^{+\infty} e^{-x^2} dx = \frac{\sqrt{\pi}}{2} \qquad (3)$

但是上面计算的是0到无穷的积分，(1)式中我们要计算的是0到某个固定值的积分。具体的讲，我们要求的积分区域如下图，正方形
S 是 $\int_0^{R} \int_0^{R} e^{-x^2-y^2} dy dx$ 的积分区域，
$\int\int_D e^{-x^2-y^2} dx dy = \pi(1-e^{-a^2})$ 中的 D
是由中心在原点、半径为 a 的圆周所围成的闭区域, 下图中 $D_1,D_2$ 是
$a=\sqrt{2}R$ 时相应 D 区域的 $\frac{1}{4}$ 。

正态分布t个标准差范围内的概率

因此

$\begin{aligned} \int\int_{D_1} e^{-x^2-y^2} dx dy < \int\int_S e^{-x^2-y^2} dx dy < \int\int_{D_2} e^{-x^2-y^2} dx dy \end{aligned}$

于是上面的不等式可以写成
$\frac{\pi}{4}(1-e^{-R^2}) < (\int_0^R e^{-x^2} dx)^2 < \frac{\pi}{4}(1-e^{-2R^2}) \qquad (4)$
但是上面这个不等式比较粗糙，我们可以构造更加精确的上下界。

对于上界，我们可以找到1/4圆面积恰好等于正方形 $R^2$ 的面积，如下图

正态分布t个标准差范围内的概率

此时圆的半径 $r_1$ 为
$\frac{\pi r_1^2}{4} = R^2 \Rightarrow r_1^2 = \frac{4R^2}{\pi}$
由于 $e^{-x^2-y^2}$ 是单调递减函数，因此必定有此上界：
$(\int_0^R e^{-x^2} dx)^2 < \frac{\pi}{4}(1-e^{-4R^2/\pi}) \qquad (5)$

对于下界，如下图，我们可以找到
$r_2 \text{到} \sqrt{2}R \text{的阴影面积}S_1 = \text{正方形面积} S-D_1$

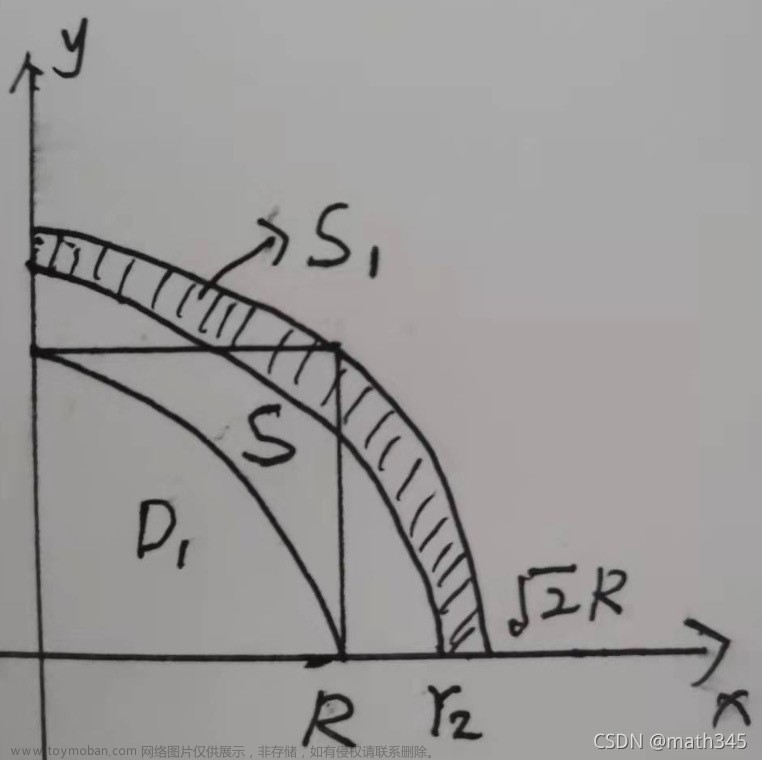
正态分布t个标准差范围内的概率

由于 $e^{-x^2-y^2}$ 是单调递减函数，因此有
$(\int_0^R e^{-x^2} dx)^2 > \int_{D_1+S_1} e^{-x^2-y^2} dx dy$
此时圆的半径 $r_2$ 为

$\begin{aligned} &R^2-\frac{\pi R^2}{4} = \frac{2\pi R^2}{4} - \frac{\pi r_2^2}{4} \\ \Rightarrow &r_2^2 = 3R^2 - \frac{4}{\pi}R^2 \end{aligned}$

因此必定有此下界：

$\begin{aligned} (\int_0^R e^{-x^2} dx)^2 &> \frac{\pi}{4}(1-e^{-R^2}) + \frac{\pi}{4}(1-e^{-2R^2}) - \frac{\pi}{4}(1 - e^{-3R^2 + \frac{4}{\pi}R^2}) \\ &> \frac{\pi}{4}(1-e^{-R^2} - e^{-2R^2} + e^{-3R^2 + \frac{4}{\pi}R^2}) \qquad (6) \end{aligned}$

合并(5)(6)式，得到了比(4)式更加精确的不等式(7)

$\begin{aligned} \frac{\pi}{4}(1-e^{-R^2} - e^{-2R^2} + e^{-3R^2 + \frac{4}{\pi}R^2}) <& (\int_0^R e^{-x^2} dx)^2 < \frac{\pi}{4}(1-e^{-4R^2/\pi}) \qquad (7)\\ \frac{\sqrt{\pi}}{2}\sqrt{(1-e^{-R^2} - e^{-2R^2} + e^{-3R^2 + \frac{4}{\pi}R^2})} <& \int_0^R e^{-x^2} dx < \frac{\sqrt{\pi}}{2}\sqrt{1-e^{-4R^2/\pi}} \qquad (8) \end{aligned}$

回到(1)式

$\begin{aligned} P(u-t\sigma \le x \le u+t\sigma) =\frac{2}{\sqrt{\pi}} \int_{0}^{\frac{t}{\sqrt{2}}} e^{-x^2} d x \end{aligned}$

在不等式(8)中，取 $R=\frac{t}{\sqrt{2}}$ ，得

$\begin{aligned} \sqrt{1-e^{-t^2/2} - e^{-t^2} + e^{-3t^2/2 + 2t^2/\pi}} < P(u-t\sigma \le x \le u+t\sigma) < \sqrt{1-e^{-2t^2/\pi}} \qquad (9) \end{aligned}$

于是写个python程序计算下

def normal_prop_lowerbound(t):
    return math.sqrt(1-math.exp(-t*t/2)-math.exp(-t*t)+math.exp(-1.5*t*t+2/math.pi * t*t))

def normal_prop_upperbound(t):
    return math.sqrt(1-math.exp(-2*t*t/math.pi))

if __name__ == '__main__':
    print(normal_prop_lowerbound(1), "< 均值为中心1个标准差范围内的概率 <", normal_prop_upperbound(1))
    print(normal_prop_lowerbound(2), "< 均值为中心2个标准差范围内的概率 <", normal_prop_upperbound(2))
    print(normal_prop_lowerbound(3), "< 均值为中心3个标准差范围内的概率 <", normal_prop_upperbound(3))

程序输出：

0.6688228555159094 < 均值为中心1个标准差范围内的概率 <
0.6862377078915619

0.9370075438591285 < 均值为中心2个标准差范围内的概率 <
0.9600223595773711

0.9945801268713956 < 均值为中心3个标准差范围内的概率 <
0.998374454827675

另外，注意到，在(9)不等式中，当我们令 R
趋于正无穷，上式两端同时趋于极限1，
从而我们也验证了正态分布的概率密度函数的积分即概率确实为1.
当然在比较粗糙的(4)不等式中，令 R
趋于正无穷，也可以验证了正态分布的概率密度函数的积分即概率确实为1.

应用场景一:
有一堆数据我们想知道是否服从正态分布，我们可以通过统计1、2、3个标准差范围内的数据的概率是否大致符合0.68，0.95，0.997的概率来校验。如果不太符合这些概率，那么就不太可能是正态分布。

应用场景二:
有一堆数据假设服从正态分布，我们想知道那些数据是异常的，那么我们就可以设定t个标准差范围内的数据是正常的，即超过t个标准差的数据即 $t\sigma$ 是异常的，取t为多少是合适的，就看我们的应用场景下的异常数据的概率有多大。