2023年祝大家兔年快乐,新年新气象,万事如意。
1.介绍
1.popCount是计算一个整数的二进制表示有多少位是1的一种算法,java有一种方法叫bitCount,也是popCount.
2.本人最近频繁遇到一些popCount的应用,所以想写一篇文章用于分享我了解的popCount.
3.本文使用Go语言进行测试,故用Go语言编写代码.
2.方法
1.暴力计算
func popCount1(num int) int {
var count int //go语言会自动初始化
for num != 0 {
if num&1 == 1 {
count++
}
num >>= 1
}
return count
}直接进行暴力循环,查找每个bit位是否是1,时间复杂度是O(n),这种方法运行的次数取决于num的位数,虽然由于是int类型,最大循环32次,但还是有很大的浪费.
2.优化循环
func popCount2(num int) int{
var count int
for num != 0 {
num &= num - 1
count++
}
return count
}解析:
假设num为7,那么二进制数值就是0111,num-1为7,二进制数值就是0110,对于&,有:
0110 & 0111 =0110
,将最后一位的1去除掉了,所以num失去了二进制的一位1,
由此循环
0101 & 0110 = 0100 , num的二进制每次失去最后一位1,直至num变为0.这种方法是我做leetcode时学到的,理解简单,使用方便,对于一些特殊的判断情况有很好的效果.leetcode相关题目地址:https://leetcode.cn/problems/two-out-of-three/
这种方法的循环次数取决于num二进制形式中1的个数,时间复杂度为O(n).
3.小修改
func popCount3(n int) int {
var count int = 32
n ^= 0xFFFFFFFF
for n != 0 {
count--
n &= n - 1
}
return count
}解析
该方法是popCount2()的变种.
0xffffffff的二进制为:11111111111111111111111111111111
n ^ 0xffffffff的作用是: 将n的0和1互换.
然后按照popCount2()的方法获取1的个数(即原本0的个数),最后按照本类型最大可能的1的数目减去获取的个数,就是原本n中1的个数注意
该方法n一开始异或的值是随类型变化的,应是本类型二进制下具有最大数量1的值.4.查表
// pc[i] is the population count of i.
var pc [256]byte
func init() {
for i := range pc {
pc[i] = pc[i/2] + byte(i&1)
}
}
// PopCount 每个8bit宽度的数字含二进制的1bit的bit个数,
// 这样的话在处理64bit宽度的数字时就没有必要循环64次,
// 只需要8次查表就可以了。
// returns the population count (number of set bits) of x.
func PopCount(x uint64) int {
return int(pc[byte(x>>(0*8))] +
pc[byte(x>>(1*8))] +
pc[byte(x>>(2*8))] +
pc[byte(x>>(3*8))] +
pc[byte(x>>(4*8))] +
pc[byte(x>>(5*8))] +
pc[byte(x>>(6*8))] +
pc[byte(x>>(7*8))])
}该方法是我在go语言圣经里学习到的,出自2.6.2. 包的初始化,这是一个汉化文本地址https://books.studygolang.com/gopl-zh/ch2/ch2-06.html
解析:
该方法将256范围内(不包括256)每个数字所有的1的个数存储起来
255的二进制为1111 1111,uint64可以拆分为8个256处理.5. bitCount(重点)
func bitCount(n uint) int {
n = n - ((n >> 1) & 0x55555555)
n = (n & 0x33333333) + ((n >> 2) & 0x33333333)
n = (n + (n >> 4)) & 0x0f0f0f0f
n = n + (n >> 8)
n = n + (n >> 16)
return int(n & 0x3f)
}第一次看见是在java的java.lang.Integer 和 java.lang.Long 类中里面,这是java里popCount的实现,而且根据我的查询,该方法出自来 Hacker's Delight第5章(如果有误望指出),
解析:
第一行
的 n = n - ((n >> 1) & 0x55555555)开始
1.1处理方法(只有2个bit的(一个单位)):
n -> 第一位为((n >> 1) & 0x1),所以 n - ((n >> 1) & 0x1)
00 -> 第一位为0,所以 00 - 00 = 00 ,有0个1
01 -> 第一位为0,所以 01 - 00 = 01 ,有1个1
10 -> 第一位为1, 所以 10 - 01 = 01 ,有1个1
11 -> 第一位为1,所以 11 - 01 = 10 ,有2个1
1.2 n >> 1 把数字向右移动一位
1.3 0x55555555 的二进制为0101 0101 0101 0101 0101 0101 0101 0101
1.4 ((n >> 1) & 0x55555555) 以2bit为一个单位,将n每一个单位上第一个bit的值清空.
1.5 n - ((n >> 1) & 0x55555555) 每个单位代表的数字就是该单位上1的数量
1.6该行的作用就是计算出一个单位所具有的1的数量,并将其存储在单位中.
1.7举例,假设n为5
0101 -> 0010 -> (0010 & 0101 = 0000) -> 0000 -> (0101 - 0000 = 0101) //得到两个单位,每个单位1的数量为1第二行
n = (n & 0x33333333) + ((n >> 2) & 0x33333333)
该操作将4个bit视为一个单位
2.1 0x33333333的二进制为0011 0011 0011 0011 0011 0011 0011 0011
2.2 (n & 0x33333333) 得到每个单位后面2个bit的1的个数
2.3 ((n >> 2) & 0x33333333) 得到每个单位前面2个bit的1的个数
2.4 (n & 0x33333333) + ((n >> 2) & 0x33333333) 将前后两个bit的1的个数相加
2.5 这行代码的目的则是为了将一单位中的1的个数加起来.一个单位中的每两个bit相加,相加的结果在储存到这一个单位二进制数中.
2.6 举例,复用上面例子:
0101 -> ((0101 & 0011) + (0001 & 0011)) -> (0001 + 0001) -> 0010 //得到一个单位,该单位1的数量为2第三行
n = (n + (n >> 4)) & 0x0f0f0f0f
将8个bit视为一个单位,
3.1 0x0f0f0f0f的二进制为0000 1111 0000 1111 0000 1111 0000 1111
3.2 (n + (n >> 4)) & 0x0f0f0f0f = (n & 0x0f0f0f0f) + ((n>>4) & 0x0f0f0f0f) 等效与第二行的内容
3.3 将数字8个bit视为一个单位,并计算每单位有多少个1
3.4 举例,继续复用上面例子:
0010 -> ((0010 + 0000) & 1111) -> 0010 //得到一个单位,该单位1的数量为2第四行
n = n + (n >> 8)
将16个bit视为一个单位,但是没有进行&运算,只有最后8位有效
4.1 举例,继续复用上面例子:
0010 - >(0010 + 0000) -> 0010
假设有第三行得到0000 0001 0000 0001
0000 0001 0000 0001 -> (0000 0001 0000 0001 + 0000 0000 0000 0001) -> 0000 0001 0000 0010第五行
n = n + (n >> 16)
将32个bit视为一个单位,同理,只有最后8位有效第六行
int(n & 0x3f)
6.1 0x3f为63,二进制为0011 1111
6.2 上面两行没有进行&(与运算),所以只有最后8位是有效的,而uint类型最大也只能有32个1,32小于63,所以只用0x3f(最后6位)即可表示
6.3最后将uint强转为int类型
6.4对于第四行和第五行为什么不& : uint类型最大1的数量不可能超过8bit表示的范围,无论是否&,都不会对最后结果产生影响,最后结果只取最后6bit的数据,若有疑问,可以自行尝试将前两行的&去除,测试并查看变化.-
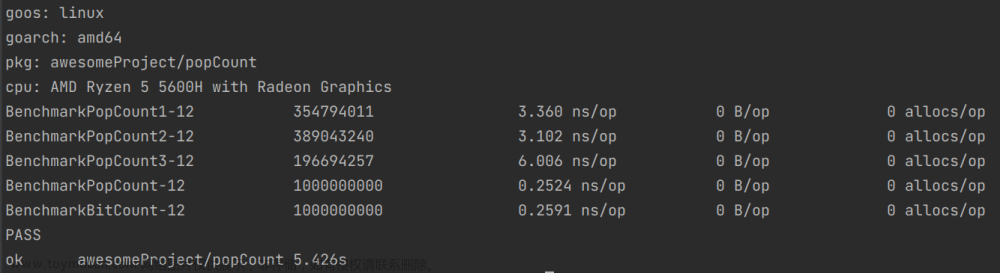
测试运行速度
ns/op 就是运行一次消耗的时间 , ns/op 列前面的一列是测试运行次数
1.测试数据:0b11111011111
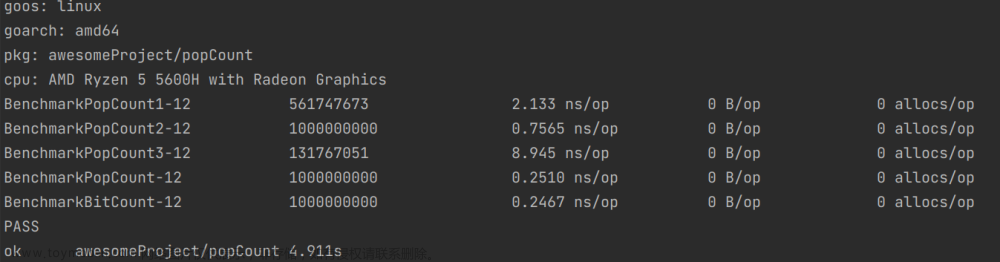
2.测试数据:0b000100000
3.测试数据:0b1

4.测试数据:0b111111111111111111111111111111111111111111111111111111111111111
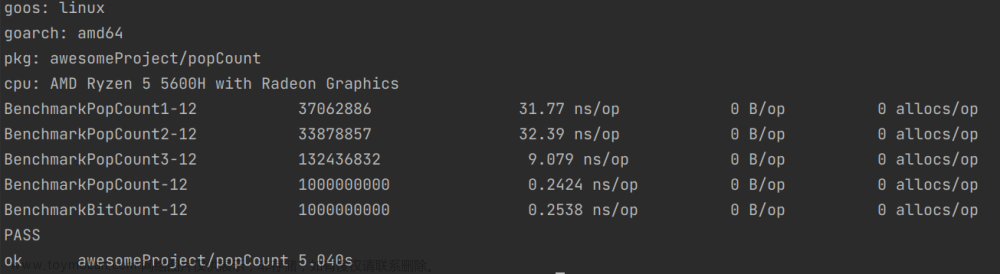
5.随机数值(0~math.MaxInt)
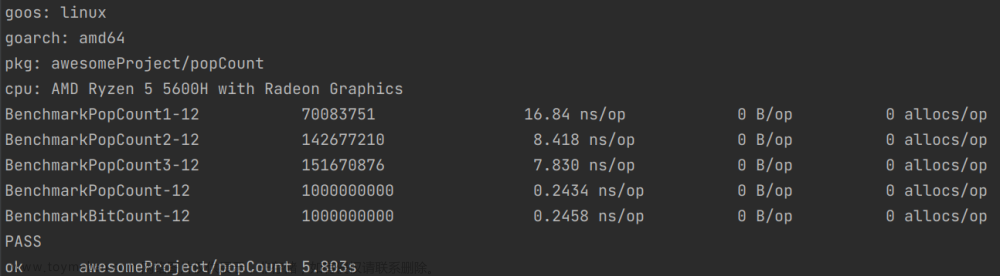
6.总结
从上述情况可以看出,一般情况下,第一种方法是最差的,第二种方法优于第一种方法,当1的数量很多时,第一种方法和第二种方法的差距就会缩小,第三种方法会优于第一种方法和第二种方法.
第四种方法和第五种方法运行速度始终相差不大,但是第四种方法占用的内存较大.
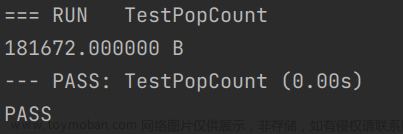
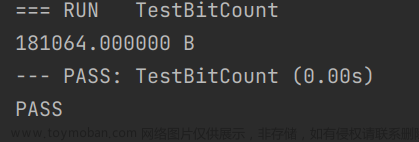
综上所述,无论什么情况下,第五种方法总是最优的
4.其他
bitCount(popCount)也是Redis的一个命令.
第五种方法也叫variable-precision SWAR算法,他的计算过程很像一棵二叉树.
还有许多其他的计算方法,但由于本人对此了解不是很多,其他方法不再讲解.
3.测试代码:
var num int
func init() {
rand.Seed(time.Now().UnixNano())
num = rand.Intn(math.MaxInt)
//num = math.MaxInt
}
func BenchmarkPopCount1(b *testing.B) {
for i := 0; i < b.N; i++ {
popCount1(num)
}
}
func BenchmarkPopCount2(b *testing.B) {
for i := 0; i < b.N; i++ {
popCount2(num)
}
}
func BenchmarkPopCount3(b *testing.B) {
for i := 0; i < b.N; i++ {
popCount3(num)
}
}
func BenchmarkPopCount(b *testing.B) {
for i := 0; i < b.N; i++ {
PopCount(uint64(num))
}
}
func BenchmarkBitCount(b *testing.B) {
for i := 0; i < b.N; i++ {
bitCount(uint(num))
}
}
func TestPopCount(t *testing.T) {
PopCount(uint64(num))
PrintMem()
}
func TestBitCount(*testing.T) {
bitCount(uint(num))
PrintMem()
}
func PrintMem() {
var mem runtime.MemStats
runtime.ReadMemStats(&mem)
fmt.Printf("%f B\n", float64(mem.Alloc))
}5.参考资料
https://www.cnblogs.com/inmoonlight/p/9301733.html
https://books.studygolang.com/gopl-zh/ch2/ch2-06.html
https://www.chessprogramming.org/Population_Count文章来源:https://www.toymoban.com/news/detail-536120.html
https://juejin.cn/post/7124182175985401863文章来源地址https://www.toymoban.com/news/detail-536120.html
到了这里,关于简单介绍popCount的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!