Leetcode：684. 冗余连接（并查集C++）

目录

684. 冗余连接

题目描述：

实现代码与解析：

并查集

原理思路：

684. 冗余连接

题目描述：

        树可以看成是一个连通且 无环 的 无向 图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：

输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：

输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

实现代码与解析：

并查集

class Solution {
public:
    int p[1010];
    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }
    vector<int> findRedundantConnection(vector<vector<int>>& edges) {

        for (int i = 0; i < edges.size() + 1; i++)  p[i] = i; // 初始化
        for (int i = 0; i < edges.size(); i++)
        {
            int a = edges[i][0];
            int b = edges[i][1];
            if(find(a) == find(b)) return edges[i];
            else p[find(a)] = find(b); // 让a的根节点的父亲节点为b的根节点，当然反过来也可以
            
        }
        return {};
    }
};

原理思路：

        并查集是看起来很难，但是是非常简单的算法，，核心代码几行就能搞定，掌握并查集算法，我们只需要了解 p数组的含义 和 find寻根函数 就差不多已经会了。

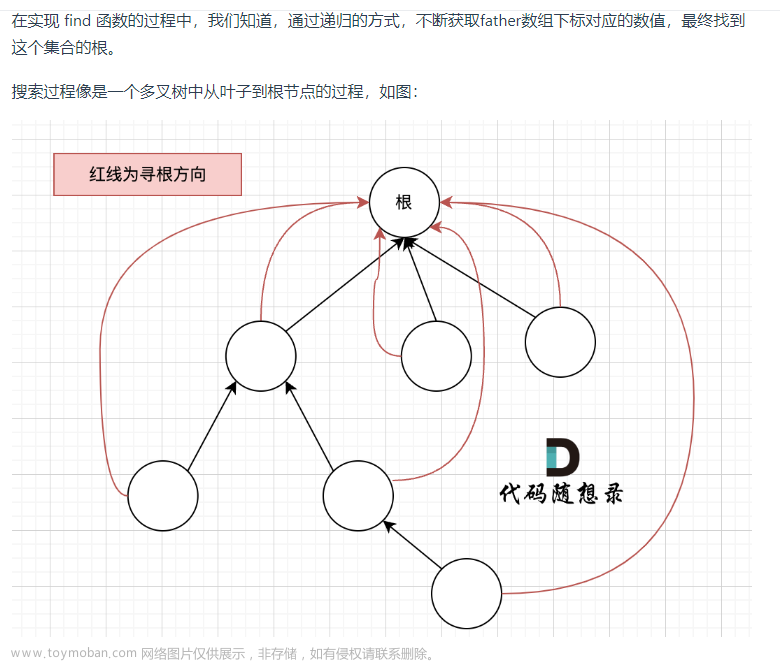
        我们把并查集的关系抽象成一颗树，相互连接的节点在一颗树上。

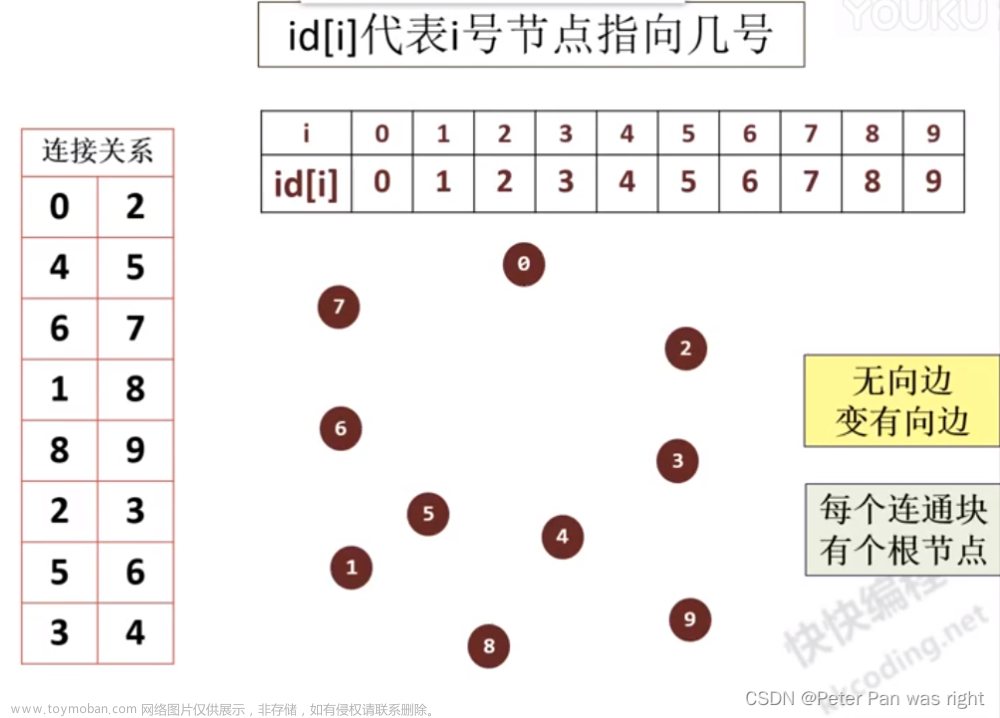
        首先 p[x] 数组的含义就是 x 节点的父亲。当 x = p[x] 时，说明其父亲节点就是自己（单独一个节点,没有相连的边），还没有去连接其关系，所以我们在初始化的时候就令其都先指向自己，也就是:

for (int i = 0; i < edges.size() + 1; i++)  p[i] = i; // 初始化

        然后就是 find(x) 函数，是用来寻找 x 节点的根节点（祖宗），并且在寻找根节点时，优化路径，使下次寻找变得非常非常快，是很关键的部分，但是代码却非常短，短短几行代码做到两件事，太优雅了。

    int find(int x)
    {
        if (p[x] != x) p[x] = find(p[x]);
        return p[x];
    }

        具体这个代码是怎么做到的，大家画个图模拟一下就知道了，这里不再讲述。

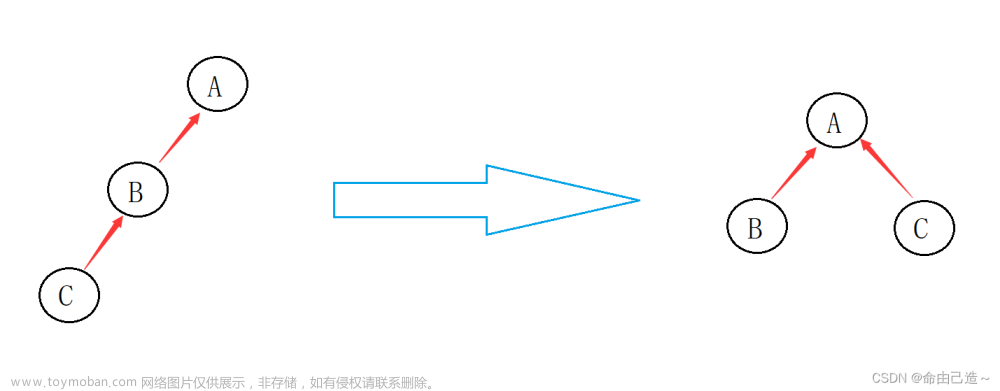
        假设一条边连接 a 和 b 节点，我们想要这两个含有 a, b节点的部分连接，只需要将a, b其中一个的根节点，作为另一个的父亲节点即可。代码如下：

p[find(a)] = find(b);

当然反过来也是可以的。

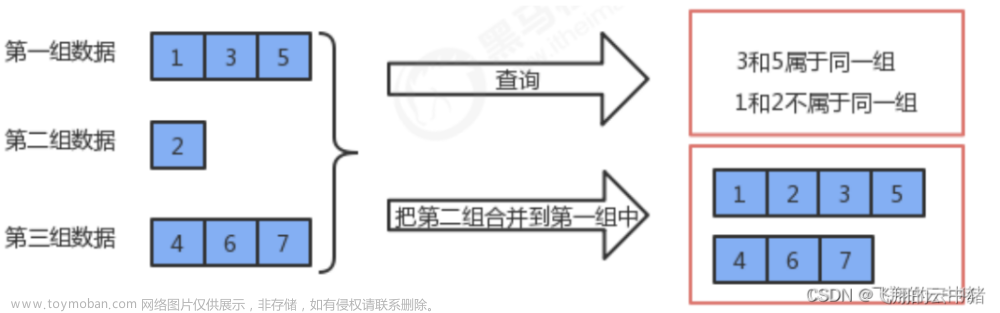
        想要判断 a, b两个节点是否联通，只需要看其根节点是否为同一个即可。代码如下：

find(a) == find(b)

        这样这道题就很简单了，我们循环遍历给的edges，若此边加入前，其相连的a, b已经联通，则此边是可以去除的。若a ,b并不联通，我们将a, b联通，进行下一次寻找，直到找到答案。文章来源地址https://www.toymoban.com/news/detail-545224.html

        for (int i = 0; i < edges.size(); i++)
        {
            int a = edges[i][0];
            int b = edges[i][1];
            if(find(a) == find(b)) return edges[i];
            else p[find(a)] = find(b); // 让a的根节点的父亲节点为b的根节点，当然反过来也可以
            
        }

到了这里，关于Leetcode：684. 冗余连接（并查集C++）的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！