leetcode 684. 冗余连接

这篇具有很好参考价值的文章主要介绍了leetcode 684. 冗余连接。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

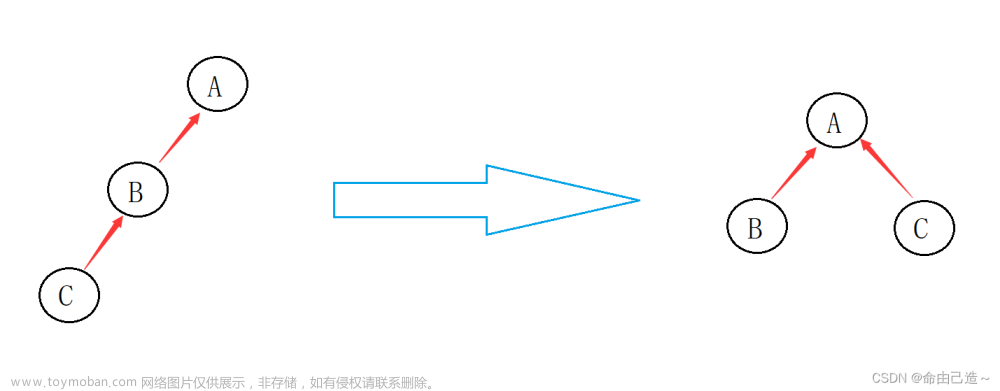
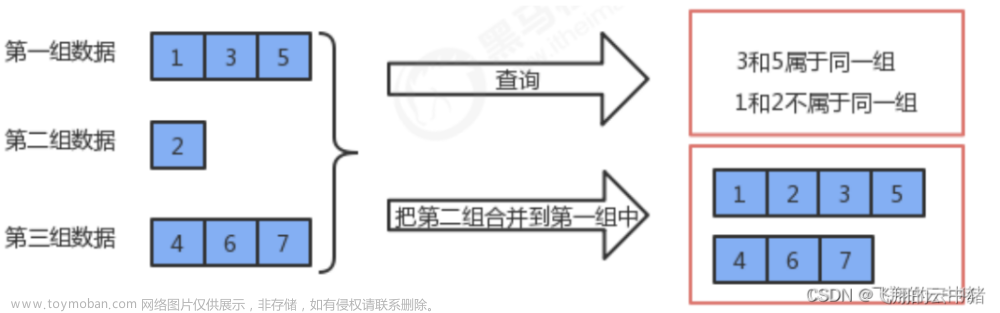
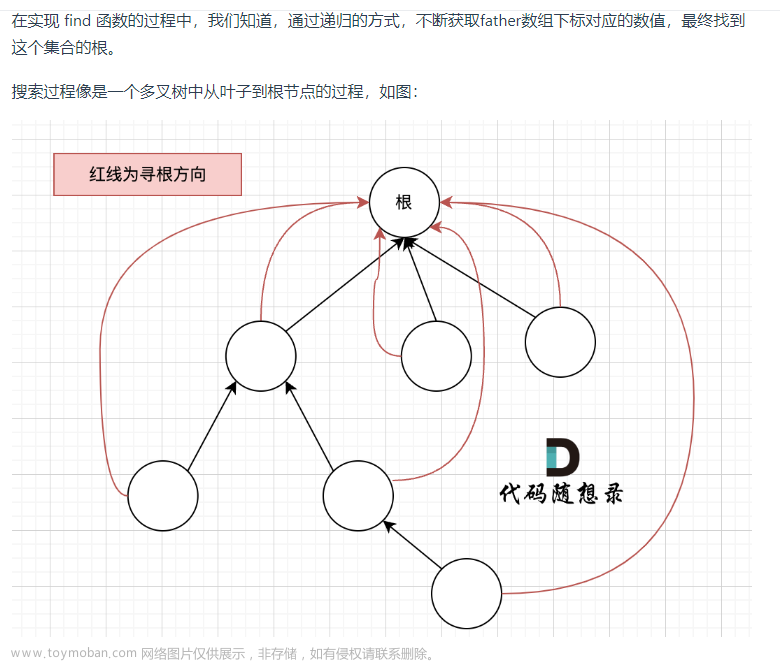
树可以看成是一个连通且无环的无向图。

给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的那个。

示例 1：
leetcode 684. 冗余连接,图,LeetCode,并查集,leetcode,算法,数据结构
输入: edges = [[1,2], [1,3], [2,3]]
输出: [2,3]

示例 2：
leetcode 684. 冗余连接,图,LeetCode,并查集,leetcode,算法,数据结构
输入: edges = [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]

提示:
n == edges.length
3 <= n <= 1000
edges[i].length == 2
1 <= ai < bi <= edges.length
ai != bi
edges 中无重复元素
给定的图是连通的
题目链接：leetcode 684

思路，可以采用并查集实现，记录每个节点的对用的最终 parent 节点，加入一条边为 (a, b)，则赋值 a 的 parent 节点为 b 的 parent 节点，如果一条边的 parent 对应节点相同，那么说明这俩节点已经在图中了。

class Solution:
    def getParent(self, parent, key):
        if parent[key] != key:
            return self.getParent(parent, parent[key])
        return key
    
    def union(self, parent, key1, key2):
        parent[self.getParent(parent, key1)] = self.getParent(parent, key2)

    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        parent = [i for i in range(len(edges)+1)]
        for x in edges:
            node1, node2 = x 
            if self.getParent(parent, node1) == self.getParent(parent, node2):
                return x
            else:
                self.union(parent, node1, node2)

方法二，直接暴力计算文章来源地址https://www.toymoban.com/news/detail-743297.html

class Solution:
    def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
        node, visited = set(), set()
        for x in edges:
            node.add(x[0])
            node.add(x[1])  
        current = set()
        visited.add(edges[0][0])
        visited.add(edges[0][1])
        vis = [0 for i in range(len(edges))]
        vis[0] = 1
        res = []
        for i in range(len(node)):
            ## 每次循环只加一个顶点进去，最后的肯定是答案
            for j in range(len(edges)):
                if vis[j] == 0:
                    x = edges[j]
                    if x[0] in visited and x[1] in visited:
                        vis[j] = 1
                        res.append(x)
                        break
                    elif x[0] in visited:
                        vis[j] = 1
                        visited.add(x[1])
                        break
                    elif x[1] in visited:
                        vis[j] = 1
                        visited.add(x[0])
                        break
            if len(res) > 0:
                return res[-1]
        return res