数学建模血管的三维重建

这篇具有很好参考价值的文章主要介绍了数学建模血管的三维重建。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

血管的三维重建

断面可用于了解生物组织、器官等的形态。例如，将样本染色后切成厚约1m m的切片，在显微镜下观察该横断面的组织形态结构。如果用切片机连续不断地将样本切成数十、成百的平行切片，可依次逐片观察。根据拍照并采样得到的平行切片数字图象，运用计算机可重建组织、器官等准确的三维形态。

假设某些血管可视为一类特殊的管道，该管道的表面是由球心沿着某一曲线（称为中轴线）的球滚动包络而成。例如圆柱就是这样一种管道，其中轴线为直线，由半径固定的球滚动包络形成。

现有某管道的相继100张平行切片图象，记录了管道与切片的交。图象文件名依次为0.bmp、1.bmp、…、99.bmp，格式均为BMP，宽、高均为512个象素（pixel）。为简化起见，假设：管道中轴线与每张切片有且只有一个交点；球半径固定；切片间距以及图象象素的尺寸均为1。

取坐标系的Z轴垂直于切片，第1张切片为平面Z=0，第100张切片为平面Z=99。Z=z切片图象中象素的坐标依它们在文件中出现的前后次序为

（-256，-256，z），（-256，-255，z），…（-256，255，z），

（-255，-256，z），（-255，-255，z），…（-255，255，z），

……

（255，-256，z），（255，-255，z），…（255，255，z）。

试计算管道的中轴线与半径，给出具体的算法，并绘制中轴线在XY、YZ、ZX平面的投影图。可能的话，利用你们的结果重新模拟切片，并评价你们模型及结果的优劣。

第2页是100张平行切片图象中的6张，全部图象请从网上（http://mcm.edu.cn）下载。

关于BMP图象格式可参考：

1.《Visual C++数字图象处理》第12页2.3.1节。何斌等编著，人民邮电出版社，2001年4月。

2.http://www.dcs.ed.ac.uk/home/mxr/gfx/2d/BMP.txt

A题：血管的三维重建

摘要

基于血管断面切片进行血管三维重建在医学领域有极为重要的意义，本文基于100张血管断面切片，采用MATLAB图像处理技术、曲线拟合方法、相似度算法等，探讨了医学血管切片的重建问题。

在中轴线与半径的确定中，本文采用寻找最大内切圆的方法，以100张血管切片作为依据，利用MATLAB对图片进行图像处理，提取出血管的轮廓、骨架，并将提取的轮廓转换为01矩阵，遍历每张图片轮廓内点到轮廓的最短距离，取最大值并求均值后得到血管内切圆半径及100个圆心坐标。计算得血管半径约为：。

在中轴线方程的求解中，本文利用100组圆心坐标数据，使用MATLAB的cftool工具箱，采用n阶多项式最小二乘方法拟合出血管中轴线方程，考虑到拟合残差、拟合系数（R2）等，确定基于LAR稳健拟合6次多项式拟合时有较好的优度，所得中轴线方程为：

$血管的三维重建数学建模,matlab,算法$

基于中轴线方程可建立三维图像及投影图像。

在血管重建相似度检验中，本文对建立的三维图像等分切割与原图对应的01矩阵进行对比，建立舍去无效像素点位的相似度算法提高计算精度，得到100组新原切片的相似度。可以发现，在0.bmp～56.bmp中相似度均达到了80%以上，在57.bmp～81.bmp中相似度均达到了70%以上，在82.bmp～91.bmp中相似度均达到了60%以上，其中第21张切片与原切片之间的相似度最高，为86.26%，第99张切片与原切片之间的相似度最低，为47.56%。整体相似度呈递减趋势。

在误差分析中，对最小二乘法的精准度进行了分析，对影响血管建模精准行性的外在影响进行了猜想，提出相性的解决方案，优化模型。

关键词：血管三维重建　　MATLAB图像处理　　最大内切圆　　稳健拟合　　多项式拟合　　相似度算法

1、问题的重述与分析

1.1问题重述

1.1.1 问题一

假设血管是由一颗球体沿一中轴线滚动包络而成的一类特殊管道，通过所提供的100张血管切面图片进行该血管的中轴线与半径的求解，并绘制中轴线在XOY、YOZ、ZOX面的投影图。

1.1.2问题二

基于问题一所求解的中轴线及半径，进行该血管的三维重建，并且结合题目所给的原信息进行重建优度的检验，比较重建血管模型与原血管模型的相似度。

1.2问题分析

1.2.1 问题一

该血管是由一颗球体滚动包络而成，那么容易知道的是在每一张切片的截面中必然存在一个最大的内切圆是该球体的直径所在截面，即每张切片中的最大内切圆圆心即为该切片与中轴线的交点，而该内切圆的半径即为该血管的半径。我们通过计算切片的最大内切圆便可进一步获得血管半径和中轴线躲在离散点集，基于曲线拟合方法对中轴线所在的离散点集进行拟合便可获得中轴线方程。获得中轴线方程后便可以直接通过MATLAB的plot函数进行投影图的绘制。

1.2.2 问题二

获得中轴线方程后，通过连续绘制离散的球体，模拟滚动包络过程，即可绘制出血管的近似三维模型，再通过分割将拟合的血管模型转换为100组01矩阵，与原血管模型的01矩阵进行比较，计算相似度，检验模型优度。

2、模型假设

（1）该血管是由一颗规则球体沿一中轴线滚动包络而成的特殊管道；

（2）血管无严重扭曲；

（3）中轴线与每个切面有且只有一个交点；

（4）血管壁的厚度忽略不计。

3、名词解释与符号说明

3.1 名词解释

（1）轮廓：图像处理中所提取图像以像素点构成的边界；

（2）robust稳健拟合：指此回归方法相对于其他回归方法而言，受异常值的影响较小。在回归分析中，自动剔除异常值，得到更为稳健的回归系数；

（3）LAR最小绝对残差拟合：LAR就是Least Absolute Residual，是一种尽可以降低残差的稳健拟合方法；

（4）二值化矩阵：即本文中提到的01矩阵，由MATLAB中的imread函数导入bmp文件所产生的一种元素只有0和1的矩阵，矩阵的每一个元素都为一个像素点，黑色为0、白色为1。

3.2 符号说明

符号	说明
R	最大内切圆半径
	血管半径
S	相似度
B	黑色像素点数
W	白色像素点数

4、模型的建立与求解

问题一：计算血管管道的中轴线与半径

4.1 对问题一的分析

由原题可知假设血管为一类特殊的管道，该管道的表面是由球心沿某一曲线（称为中轴线）的球滚动包络而成，并且管道中轴线与每张切片有且只有一个交点。因此可以得出结论：切片中最大内切圆圆心即为切片与中轴线的交点，最大内切圆半径即为血管半径。于是需要找100张图片的最大内切圆圆心，通过方法得出中轴线方程。

4.2 对问题一的求解

（1）将图片转化为数据

使用MATLAB软件调用imread、imshow函数将100张切片的bmp图像录入到MATLAB中,并将其转化为512*512*100的三维0-1矩阵，其中1代表黑色像素点，0代表白色像素点。在每一个512*512像素的图像中，每一个像素都有一个确定的坐标，可以找出这100张图片的像素矩阵；

（2）求切片的轮廓与骨架

调用MATLAB中的内部函数edge可以得到所有切片的轮廓线；

（3）求出每个切片最大内切圆的半径

对切片内部任意一个点，求出它到轮廓线上所有点的距离，并取其最小值，由于所有内点都对应一个最小值，在这些最小值中取最大值，即为：最大内切圆的半径；

假设切片内部有P个点，第i个点的坐标为，切片轮廓线上有个q点，第j个点的坐标为,则切片内部第点到轮廓线上第点的距离为：

第j个点对应的最小距离：

其中，j=1,2,3.....

即最大内切圆的半径为：

其中，i=1,2,3,....

（4）求最大内切圆平均值

将100个切片所对应的最大内切圆半径求取平均值，即为：血管的半径

（5）使用n次多项式最小二乘拟合中轴线方程

在此前的步骤中我们已经获得了血管的近似半径及中轴线所在离散点集（即圆心），针对这100组圆心我们计划使用拟合方法进行中轴线方程的建立。进行了1～9阶的多项式拟合后发现其拟合优度均不太好（残差平方和SSE>10000），考虑到血管结构是一个客观已知的具象事物而非数据走势，我们需要尽可能多的降低残差来提高与原血管的一致程度，所以我们在原先的n次多项式二乘拟合的基础上，使用了LAR稳健拟合（LAR：Least Absolute Residual（最小绝对残差）），通过使用这种方法，我们发现6次多项式的SSE降至3000左右，相较来说拟合优度较高。

拟合的中轴线参数方程为：

$血管的三维重建数学建模,matlab,算法$

4.3 MATLAB求解

4.3.1 最大内切圆圆心及半径求解

首先在MATLAB中利用imread函数和imshow函数画出切片的轮廓点（具体程序见附录），接着调用内部函数edge得到所有切片的轮廓线，求出了切片内部的点到轮廓上点的最小距离，在这些最小值中取最大值，即为最大内切圆的半径。（具体程序见附录二）100张切片最大内切圆的圆心坐标及半径如表一所示：

表1：100张切片最大内切圆的圆心坐标及半径

切片序号	最大内切圆圆心坐标			最大内切圆半径	切片序号	最大内切圆圆心坐标			最大内切圆半径
	x	y	z			x	y	z
0	-160	1	1	29.06888371	51	-114	117	52	29.69848481
1	-160	0	2	28.28427125	52	-113	118	53	29.69848481
2	-160	2	3	29.01723626	53	-112	119	54	29.69848481
3	-160	2	4	29.06888371	54	-111	120	55	29.68164416
4	-160	2	5	29.06888371	55	-111	120	56	29.20616373
5	-160	2	6	29.06888371	56	-63	151	57	29.41088234
6	-160	1	7	29	57	-75	145	58	29.52964612
7	-160	4	8	29.01723626	58	-81	142	59	29.52964612
8	-160	1	9	29	59	-51	156	60	29.54657341
9	-160	1	10	28.86173938	60	-51	156	61	29.54657341
10	-160	7	11	28.86173938	61	-31	162	62	29.61418579
11	-160	8	12	28.86173938	62	-31	162	63	29.61418579
12	-160	9	13	28.86173938	63	-31	162	64	29.61418579
13	-160	10	14	29.01723626	64	-35	161	65	29.61418579
14	-160	12	15	29.01723626	65	-35	161	66	29.61418579
15	-160	13	16	29.01723626	66	-26	163	67	29.42787794
16	-160	14	17	29.01723626	67	-35	161	68	29.41088234
17	-160	16	18	29.01723626	68	-26	163	69	29.27456234
18	-160	17	19	29.01723626	69	46	163	70	29.42787794
19	-160	18	20	29.01723626	70	46	163	71	29.61418579
20	-160	19	21	29.01723626	71	46	163	72	29.61418579
21	-160	20	22	29.01723626	72	46	163	73	29.61418579
22	-160	21	23	29.01723626	73	65	158	74	29.61418579
23	-160	22	24	29.01723626	74	68	157	75	29.73213749
24	-160	21	25	29.06888371	75	65	158	76	29.73213749
25	-160	21	26	29.06888371	76	81	152	77	29.54657341
26	-160	21	27	29.06888371	77	81	152	78	29.52964612
27	-159	30	28	29.15475947	78	81	152	79	29.52964612
28	-159	30	29	29.27456234	79	135	118	80	29.41088234
29	-159	29	30	29.27456234	80	136	117	81	29.69848481
30	-158	35	31	29.42787794	81	136	117	82	29.69848481
31	-157	40	32	29.61418579	82	137	116	83	29.69848481
32	-157	40	33	29.61418579	83	138	115	84	29.69848481
33	-157	40	34	29.61418579	84	138	115	85	29.69848481
34	-156	44	35	29.61418579	85	139	114	86	29.69848481
35	-153	55	36	29.73213749	86	139	114	87	29.69848481
36	-153	55	37	29.73213749	87	139	114	88	29.69848481
37	-153	55	38	29.73213749	88	140	113	89	29.69848481
38	-152	58	39	29.73213749	89	140	113	90	29.68164416
39	-152	58	40	29.61418579	90	172	67	91	29.52964612
40	-150	63	41	29.54657341	91	172	67	92	29.52964612
41	-149	66	42	29.54657341	92	172	67	93	29.52964612
42	-148	68	43	29.52964612	93	172	67	94	29.52964612
43	-148	68	44	29.52964612	94	182	43	95	29.73213749
44	-143	78	45	29.52964612	95	187	24	96	29.61418579
45	-137	88	46	29.41088234	96	187	24	97	29.61418579
46	-137	88	47	29.41088234	97	187	24	98	29.61418579
47	-116	115	48	29.69848481	98	187	24	99	29.61418579
48	-115	116	49	29.69848481	99	188	18	100	29.42787794

即血管的半径为：

4.3.2 中轴线拟合

在3.1中我们已经获得了每张切片照片中最大内切圆的圆心，即中轴线所在离散点集，通过对这组离散点集进行拟合就可以获得近似的中轴线方程。

我们借助cftool工具箱对z-x、z-y分别进行n次多项式拟合，并观察SSE与R2考察拟合的优度。

表2：z-x多项式拟合优度比较

多项式拟合阶数	稳健拟合（LAR）	R-square	SSE	多项式拟合阶数	稳健拟合（LAR）	R-square	SSE
2	否	0.9634	6.28e+04	6	否	0.9934	1.126e+04
2	是	0.997	5196	6	是	0.9978	3704
3	否	0.9739	4.483e+04	7	否	0.9939	1.041e+04
3	是	0.9709	4.985e+04	7	是	0.9976	4062
4	否	0.9912	1.504e+04	8	否	0.994	1.022e+04
4	是	0.9982	3009	8	是	0.9973	4574
5	否	0.9913	1.498e+04	9	否	0.9946	9323
5	是	0.9977	3965	9	是	0.9973	4661

表3：y-z多项式拟合优度比较

多项式拟合阶数	稳健拟合（LAR）	R-square	SSE	多项式拟合阶数	稳健拟合（LAR）	R-square	SSE
2	否	0.7154	9.532e+04	6	否	0.9819	6055
2	是	0.7066	9.828e+04	6	是	0.9941	1991
3	否	0.968	1.072e+04	7	否	0.9837	5473
3	是	0.966	1.137e+04	7	是	0.9936	2136
4	否	0.969	1.038e+04	8	否	0.9837	5451
4	是	0.9645	1.191e+04	8	是	0.9927	2439
5	否	0.9817	6122	9	否	0.9847	5127
5	是	0.9814	6232	9	是	0.9923	2564

对比上述几种多项式拟合的R方与SSE可以发现，在6次多项式的LAR稳健拟合中，拟合优度相对最好，使用MATLAB的cftool工具箱输出其多项式系数并整理成x与y关于z的参数方程。

图1、2：cftool工具箱进行基于LAR的6阶多项式拟合

血管的三维重建数学建模,matlab,算法

则6次多项式拟合得到的近似中轴线方程为：

$血管的三维重建数学建模,matlab,算法$

使用MATLAB作图可得计算所得的中轴线所在点集与拟合曲线关系，可以发现拟合效果较好。

图3：拟合中轴线与圆心点对比图

血管的三维重建数学建模,matlab,算法

4.3.3 中轴线投影

通过MATLAB的polyval函数对多项式进行求值绘图，然后使用plot函数直接绘制投影图即可：

图4、5、6、7：拟合中轴线的三维图与投影图

血管的三维重建数学建模,matlab,算法

问题二：血管管道的三维重建与相似度分析

4.4 对问题二的分析

在问题一中我们已经拟合出了中轴线的近似方程，根据该方程以及血管半径进行血管的三维重建，然后根据还原后的血管三维图像进行模拟切片操作，输出一系列新的血管切片图片，得到在本模型下的100张拟合血管切片，与原血管切片进行相似度分析。

4.5 对问题二的求解

4.5.1 血管三维重建

基于题目假设，该血管是由一个球体滚动包络而成，而该球体的半径及球心轨迹线方程（中轴线方程）已经求得，我们将该球体沿着中轴线滚动绘图，即可获得拟合血管的三维重建图。

图8、9：血管三维重建图

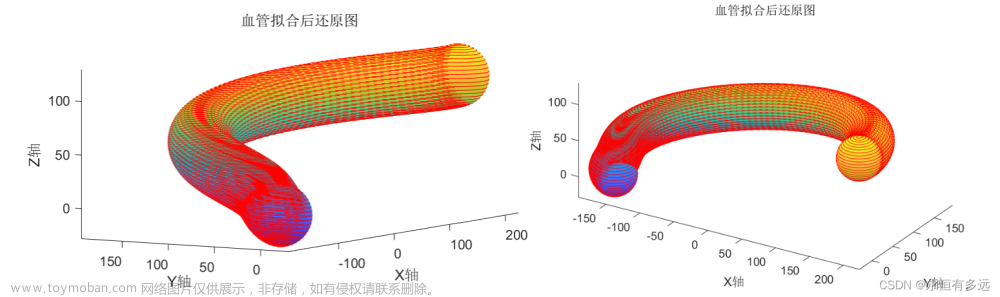
血管的三维重建数学建模,matlab,算法

4.5.2 复原血管切片

在重新进行血管切片时，我们考虑到重建的血管模型是由一颗半径确定的球体沿着中轴线滚动形成的包络面，那么该血管具有的一项特征就是中轴线上的点与血管壁之间的最短距离应为所求的血管半径，那么就可以通过遍历该512*512*100的像素单位空间内所有的像素点距离中轴线的最短距离以寻找到处于血管壁的像素点，寻找到血管壁以后其内部的所有像素点均为血管内部结构，使用1表示白色，0表示黑色，将对应血管壁内外使用0、1填充，转换为图像结即可得到复原的血管切片。

4.5.3 相似性检验

检验相似性主要基于对于原血管切片与重建血管切片的像素点位进行对比分析，我们通过输出两组切片的二值化矩阵，对比对应点位等值情况进行相似度的计算。

设相似度为S，黑色像素点数为B,白色像素点数为W，则：

$血管的三维重建数学建模,matlab,算法$

其中B+W=512x512。

在实际考察中，我们发现黑白像素点的数量差较大，这种情况会一定程度上影响相似度的计算，所以我们从算法上考虑将在切片中无关区域进一步消除。

改进方法为将两组血管切片的二值化矩阵相加，产生一组新的矩阵，这组矩阵由0、1、2组成，其中：

当像素点位值为0时，表示原血管切片与重建血管切片的对应位置均为黑色，是构成血管模型的点位，该点有效，记该点数量为True；
当像素点位值为1时，表示原血管切片与重建血管切片的对应位置黑色与白色各有一项，这意味着重建的血管模型与原血管模型存在误差，是模型的误差点，该点有效,记该点数量为False；
当像素点位值为2时，表示原血管切片与重建血管切片的对应位置均为白色，是不影响血管模型的无关点位，应舍去不考虑。

此时，相似度表示为：

$血管的三维重建数学建模,matlab,算法$

注：这里的公式当时思考有偏差，应该优化为01对比，（ture为相同个数，n为总数量）

将本算法代入MATLAB对两组切片编程求解，得到以下每张切片对应的相似度分布。

表4：100组切片的相似度比较表

切片序号	相似度	切片序号	相似度	切片序号	相似度	切片序号	相似度
0	0.8081	25	0.8429	50	0.8202	75	0.7460
1	0.8242	26	0.8360	51	0.8182	76	0.7399
2	0.8375	27	0.8306	52	0.8137	77	0.7345
3	0.8425	28	0.8249	53	0.8105	78	0.7282
4	0.8495	29	0.8190	54	0.8066	79	0.7213
5	0.8541	30	0.8152	55	0.8038	80	0.7141
6	0.8578	31	0.8110	56	0.8002	81	0.7068
7	0.8600	32	0.8063	57	0.7976	82	0.6991
8	0.8579	33	0.8048	58	0.7934	83	0.6915
9	0.8588	34	0.8038	59	0.7923	84	0.6825
10	0.8592	35	0.8029	60	0.7884	85	0.6737
11	0.8580	36	0.8038	61	0.7862	86	0.6650
12	0.8592	37	0.8063	62	0.7852	87	0.6552
13	0.8586	38	0.8089	63	0.7833	88	0.6452
14	0.8575	39	0.8127	64	0.7806	89	0.6341
15	0.8589	40	0.8166	65	0.7780	90	0.6225
16	0.8584	41	0.8221	66	0.7764	91	0.6103
17	0.8592	42	0.8258	67	0.7736	92	0.5969
18	0.8608	43	0.8285	68	0.7701	93	0.5825
19	0.8611	44	0.8301	69	0.7678	94	0.5672
20	0.8611	45	0.8305	70	0.7666	95	0.5505
21	0.8626	46	0.8310	71	0.7633	96	0.5316
22	0.8615	47	0.8294	72	0.7603	97	0.5133
23	0.8591	48	0.8257	73	0.7561	98	0.4948
24	0.8519	49	0.8230	74	0.7514	99	0.4756

可以发现，在0.bmp～56.bmp中相似度均达到了80%以上，在57.bmp～81.bmp中相似度均达到了70%以上，在82.bmp～91.bmp中相似度均达到了60%以上，其中第21张切片与原切片之间的相似度最高，为86.26%，第99张切片与原切片之间的相似度最低，为47.56%。

显然，该模型的拟合程度在血管中前段具有较好的拟合效果，但是在尾段的拟合效果越来越差。

5、模型评价

5.1 优点

①本模型较好地利用到题设给出的小球滚动包络形成地血管这一特点，使用MATLAB中的edge函数、imread函数、imshow函数等对题目给出的血管切片图进行二值化、轮廓化，通过计算内点至轮廓的最短距离，极大地简化了寻找最大内切圆圆心和半径的过程；

②在拟合中轴线方程时，充分考虑到血管这一具体事物的客观性，在进行拟合时应尽可能多的降低残差，以充分接近原模型，本模型使用6次多项式LAR稳态拟合，充分降低了残差平方和，使模型与原血管的契合度提高；

③在计算相似性时充分考虑到无关像素点会对相似度的影响性，舍去无关区域在计算中的部分，充分提高了相似度计算的精确度和客观性。

5.2 缺点

①虽然拟合优度有进一步提高，但是实际的重建相似度仍有较大出入，尤其在重建血管的尾段，误差逐渐增大，如何寻找到更好的拟合方法进一步提高血管重建的精度，这是需要进一步探讨和研究的；

②血管的重建模型虽然直观地表现出来了，但是并没能通过一组具体的数学方程进行表示，实际上血管模型仍然是离散的而非连续的，如何找到合适的方法基于中轴线和滚动球体建立曲面方程，这是有待学习的。

6、参考文献

[1] David Kincaid, Ward Cheney,王国荣,俞耀明,徐兆亮,[数值分析],机械工业出版社.

[2] 司守奎,孙兆亮,[数学建模算法与应用],国防工业出版社,第二版.

[3] 胡小峰,赵辉,[Visual C+++/MATLAB图像处理与识别使用案例精选],人民邮电出版社.

7、附录

7.1 轮廓提取

%轮廓提取

clc;

clear all;

image = dir('C:\Users\math\Desktop\A01bmp\');% 路径为原切片存储路径

files = dir(fullfile('C:\Users\math\Desktop\A01bmp\','*.bmp'));% 处理的图片格式为bmp

lengthFiles = length(files);

A=cell(lengthFiles,1);% 用cell来存储每个图片所对应的矩阵

for i = 1:lengthFiles

Img = imread(strcat('C:\Users\math\Desktop\A01bmp\',files(i).name));%文件所在路径

A{i,1}=Img;

disp(strcat('C:\Users\math\Desktop\A01bmp\',files(i).name)) %打印文件路径

imshow(Img)

end文章来源地址https://www.toymoban.com/news/detail-599919.html

for tt=1:lengthFiles

if length(size(A{tt,1}))==3

A{tt,1}=A{tt}(:,:,1);

end

7.2 求解半径

%求半径

%创建一个101*4的矩阵

tx=zeros(101,4);

for d=0:99

%将整形转换成字符串函数，并用字符串连接函数将两个字符串连接起来

k=strcat('C:\Users\math\Desktop\A01bmp\',int2str(d),'.bmp');

A=imread(k);%A变量表示每一个图片

for i=1:1:512

for j=1:1:512

A(i,j)=1-A(i,j);% 变为灰度图片

end

BW=edge(A,'sobel');%自动选择阈值用Sobel算子进行边缘检测

BW2=bwmorph(A,'skel',inf);% 提取图像A的骨架，n = Inf时，移除目标边界孤立像素，保留下来的像素组合成图像的骨架

[x,y,z]=find(BW);% 找到非0元素

[a,b,c]=find(BW2);

m=length(a);%BW2

n=length(x);%BW

e=zeros(m,n);

f=zeros(m,2);

for i=1:m

for j=1:n

p1=a(i);%BW2

q1=b(i);

p2=x(j);%BW

q2=y(j);

e(i,j)=sqrt((p1-p2)^2+(q1-q2)^2);% 内部点到边缘轮廓线上点的距离

end

[zr,zxh]=min(e(i,:)); %内部点到边缘点的距离中取最小值

f(i,1)=zr; %重新赋值给f变量

f(i,2)=zxh;

end

[zR,zxxh]=max(f(:,1));% 这些最小值中取最大值，即为最大内切圆的半径

x=a(zxxh)-256; %默认以图片中间为圆心坐标

y=b(zxxh)-256;

tx(d+1,1)=x;% 圆心横坐标

tx(d+1,2)=y;% 圆心纵坐标

tx(d+1,3)=d+1; %第几幅图片

tx(d+1,4)=zR; %最大内切圆的半径

end

7.3 中轴线及投影绘制

clear;

clc;

x=[-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-160;-159;-159;-159;-158;-157;-157;-157;-156;-153;-153;-153;-152;-152;-150;-149;-148;-148;-143;-137;-137;-116;-115;-115;-114;-114;-113;-112;-111;-111;-63;-75;-81;-51;-51;-31;-31;-31;-35;-35;-26;-35;-26;46;46;46;46;65;68;65;81;81;81;135;136;136;137;138;138;139;139;139;140;140;172;172;172;172;182;187;187;187;187;188;];

y=[1;0;2;2;2;2;1;4;1;1;7;8;9;10;12;13;14;16;17;18;19;20;21;22;21;21;21;30;30;29;35;40;40;40;44;55;55;55;58;58;63;66;68;68;78;88;88;115;116;116;117;117;118;119;120;120;151;145;142;156;156;162;162;162;161;161;163;161;163;163;163;163;163;158;157;158;152;152;152;118;117;117;116;115;115;114;114;114;113;113;67;67;67;67;43;24;24;24;24;18;];

z=[1;2;3;4;5;6;7;8;9;10;11;12;13;14;15;16;17;18;19;20;21;22;23;24;25;26;27;28;29;30;31;32;33;34;35;36;37;38;39;40;41;42;43;44;45;46;47;48;49;50;51;52;53;54;55;56;57;58;59;60;61;62;63;64;65;66;67;68;69;70;71;72;73;74;75;76;77;78;79;80;81;82;83;84;85;86;87;88;89;90;91;92;93;94;95;96;97;98;99;100;];

format long

px = [1.094e-08 -3.426e-06 0.0003765 -0.0172 0.3513 -2.961 -152.8];

py = [9.575e-09 -2.31e-06 0.0001792 -0.005143 0.07317 0.3531 -0.9604];

x1=polyval(px,z);

y1=polyval(py,z);

figure(1);

plot3(x1,y1,z)

grid on

xlabel('X轴');

ylabel('Y轴');

zlabel('Z轴');

title('中轴线图');

figure(2);

plot(z,x1,'-r')

ylabel('Z轴');

xlabel('X轴');

title('中轴线XOZ平面投影图');

grid on

figure(3);

plot(z,y1,'-b')

xlabel('Z轴');

ylabel('Y轴');

title('中轴线YOZ平面投影图');

grid on

figure(4);

plot(x1,y1,'-')

xlabel('X轴');

ylabel('Y轴');

title('中轴线XOY平面投影图');

grid on

7.4 血管重建

plot3(x,y,z,'+');

hold on

px = [1.094e-08 -3.426e-06 0.0003765 -0.0172 0.3513 -2.961 -152.8];

py = [9.575e-09 -2.31e-06 0.0001792 -0.005143 0.07317 0.3531 -0.9604];

x1=polyval(px,z);

y1=polyval(py,z);

ball=zeros(100,3);

ball(:,1)=x1; ball(:,2)=y1; ball(:,3)=z;

t=linspace(0,pi,25);

p=linspace(0,2*pi,25);

[theta,phi]=meshgrid(t,p);

for i=1:100

x=29.4166*sin(theta).*sin(phi)+ball(i,1);

y=29.4166*sin(theta).*cos(phi)+ball(i,2);

z=29.4166*cos(theta)+ball(i,3);

hold on

surf(x,y,z);

plot3(x,y,z,'red')

axis equal;

end

xlabel('X轴');

ylabel('Y轴');

zlabel('Z轴');

title('血管拟合后还原图');

hold off

shading interp

7.5 重建血管切片

R=29.4166;

z=1:100;

x=1.094e-08.*(z-1).^6-3.426e-06.*(z-1).^5+0.0003765.*(z-1).^4-0.0172.*(z-1).^3+0.3513.*(z-1).^2-2.961.*(z-1)-152.8;

% x与t的函数关系式

y=9.575e-09.*(z-1).^6-2.31e-06.*(z-1).^5+0.0001792.*(z-1).^4-0.005143.*(z-1).^3+0.07317.*(z-1).^2+0.3531.*(z-1)-0.9604;

% y与t的函数关系式

for m=0:99 % m代表切片层数

a=ones(512,512);%存储截面图象灰度矩阵，全1纯白

for i=1:512%通过遍历i、j、p来遍历空间所有点

for j=1:512

for p=1:100

%空间点的坐标位置遍历，血管内部的点肯定大于（黑），外部（白）

b(p)=sqrt(((i-257)-x(p))^2+((j-257)-y(p))^2+(m+1-p)^2);

end

if min(b)<=R %当该点到同高度下中轴点的距离小于R时，即在血管内部

a(i,j)=0; %染成黑色

end

imwrite(a,strcat('C:\Users\Regulus\Desktop\数模训练\切片',int2str(m),'.bmp'));

%输出切片后的图像

end

7.6 相似性检验

clear;

clc;

str1='C:\Users\Regulus\Desktop\数模训练\切片比较\老切片\ ';

str2='C:\Users\Regulus\Desktop\数模训练\切片比较\新切片\ ';

for o = 1:1:100

p=o-1;

P1=imread([str1,num2str(p),'.bmp']); %读取原切片

P2=imread([str2,num2str(p),'.bmp']); %读取新切片

P=P1+im2bw(P2); %二值化（矩阵相加）

Ture=0; %记录像素为0的点（黑点）

False=1; %记录像素为1的点（白点）

[h,w]=size(P); %读取新矩阵的尺寸

%遍历比较

for i=1:h

for j=1:w

if P(i,j)==0

Ture=Ture+1;

elseif P(i,j)==1

False=False+1;

end

S(o,1)=double(Ture)/(Ture+False);

end

到了这里，关于数学建模血管的三维重建的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

Toy模板网

数学建模血管的三维重建

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

微信扫一扫打赏

支付宝扫一扫领取红包，优惠每天领

二维码1

二维码2