1. Toy模板网首页
  2. > Toy博客

第5章：神经网络

6月前 作者：why151 分类：Toy博客 阅读(3) 违法举报

这篇具有很好参考价值的文章主要介绍了第5章：神经网络。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

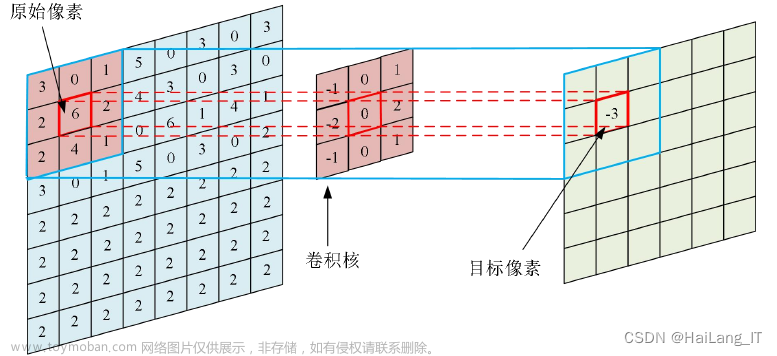
神经元模型

第5章：神经网络,机器学习,神经网络,人工智能,深度学习
上述定义的简单单元即为神经元模型。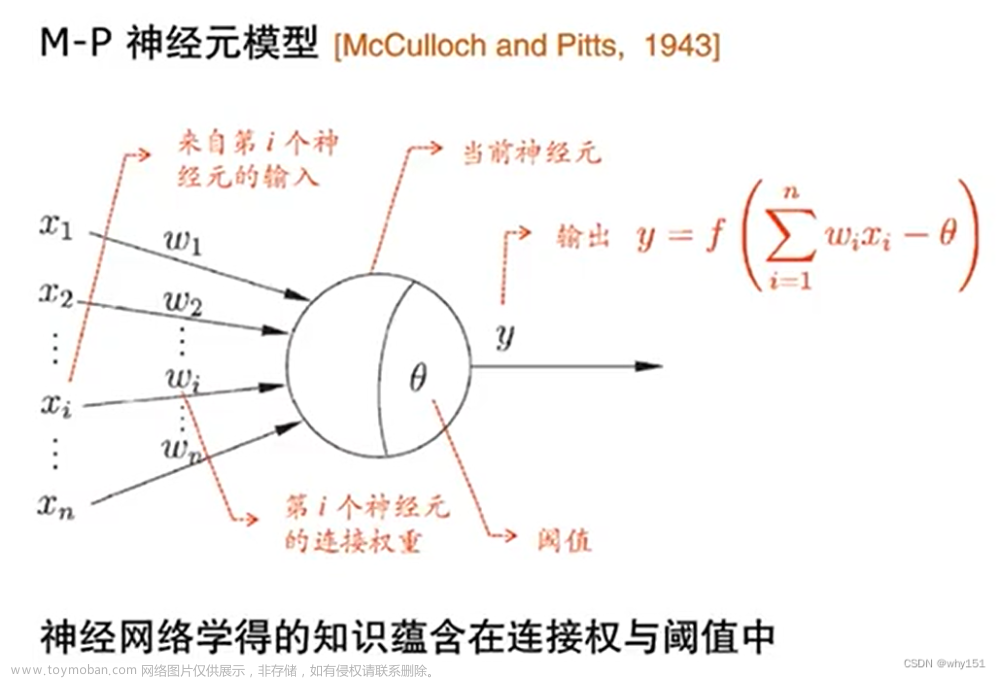
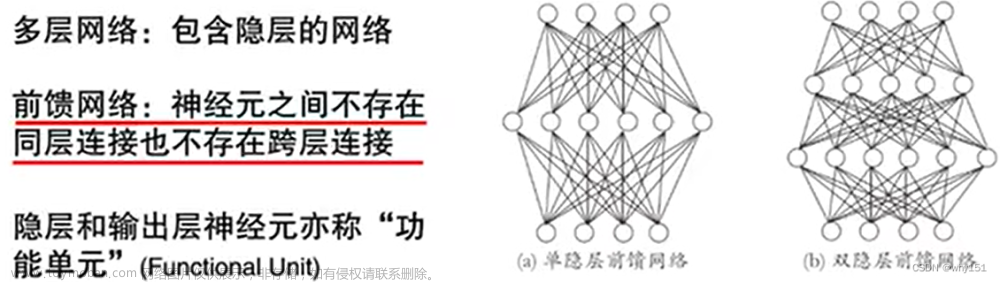
第5章：神经网络,机器学习,神经网络,人工智能,深度学习
第5章：神经网络,机器学习,神经网络,人工智能,深度学习

多层网络

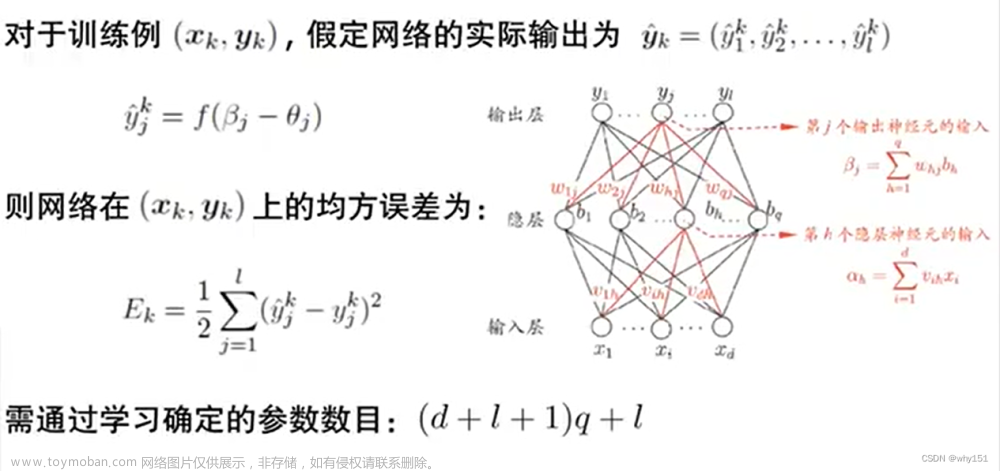
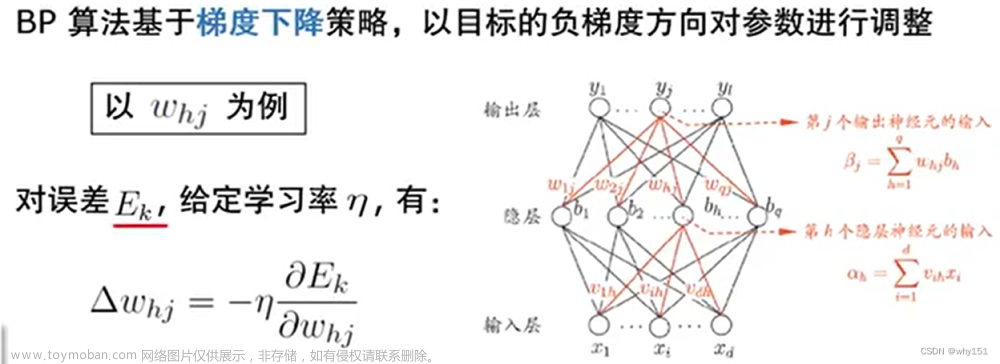
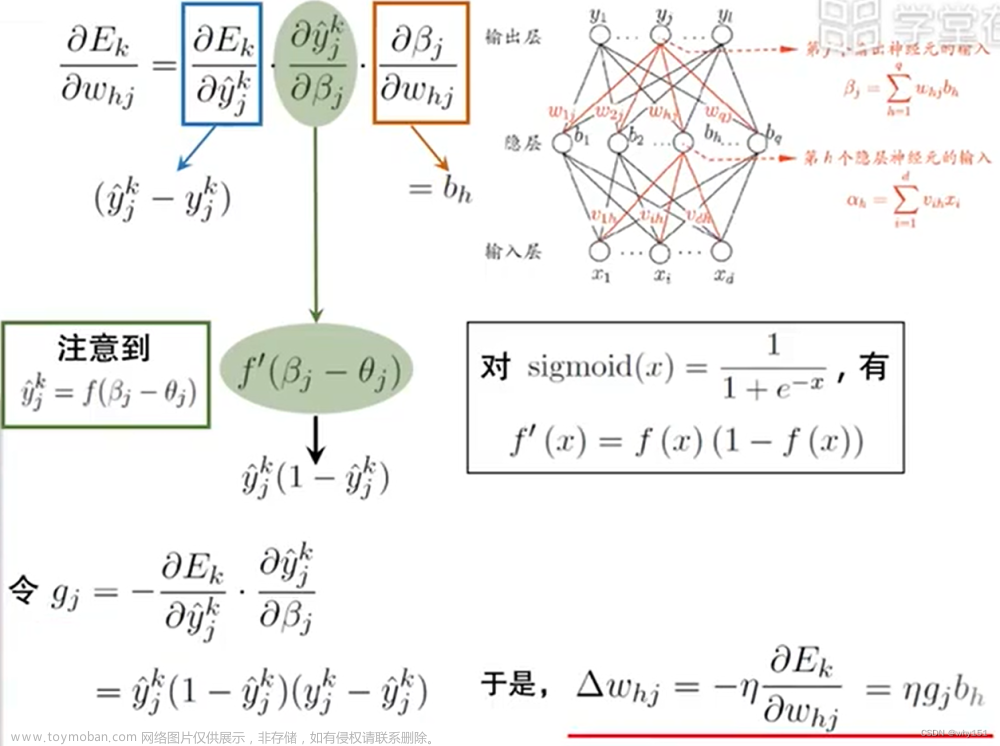
第5章：神经网络,机器学习,神经网络,人工智能,深度学习
第5章：神经网络,机器学习,神经网络,人工智能,深度学习
第5章：神经网络,机器学习,神经网络,人工智能,深度学习

误差逆传播算法

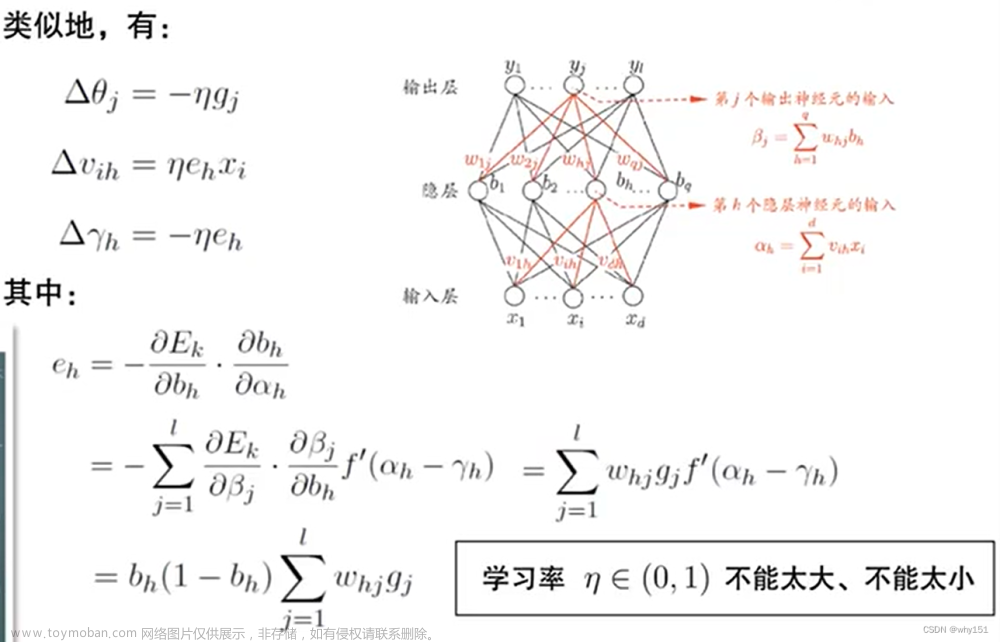
第5章：神经网络,机器学习,神经网络,人工智能,深度学习
第5章：神经网络,机器学习,神经网络,人工智能,深度学习
第5章：神经网络,机器学习,神经网络,人工智能,深度学习
第5章：神经网络,机器学习,神经网络,人工智能,深度学习
第5章：神经网络,机器学习,神经网络,人工智能,深度学习

  • 标准BP算法：参数更新非常频繁，可能出现抵消现象。
  • 积累BP算法：下降到一定程度上，进行下一步会非常缓慢。

过拟合

  • 早停：划分训练集和验证集，若训练集误差降低而验证集升高则停止训练。
  • 正则化：在误差目标函数中加入一个用于描述网络复杂度的部分， E = λ 1 m ∑ k = 1 m E k + ( 1 − λ ) ∑ i w i 2 E=\lambda\frac{1}{m}\sum_{k=1}^mE_k+(1-\lambda)\sum_iw_i^2 E=λm1​∑k=1m​Ek​+(1−λ)∑i​wi2​

全局最小与局部极小

  • 局部极小解：是参数空间的某个点，其邻域点的误差函数值均不小于该点的误差函数值，可能存在多个。
  • 全局极小解：是指参数空间中所有点的误差函数值均不小于该点的误差函数值，只存在一个。

如何跳出局部极小值点？文章来源地址https://www.toymoban.com/news/detail-647894.html

  • 以多组不同参数值初始化多个神经网络，取误差最小的解。
  • 使用模拟退火，在每一步都有一定概率接受比当前解更差的算法。
  • 使用随机梯度下，即便陷入局部极小点，它计算出来的梯度仍然可能不为0。
    第5章：神经网络,机器学习,神经网络,人工智能,深度学习

到了这里，关于第5章：神经网络的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处： 如若内容造成侵权/违法违规/事实不符，请点击违法举报进行投诉反馈，一经查实，立即删除！

分享到：
领支付宝红包 赞助服务器费用

相关文章

觉得文章有用就打赏一下文章作者

支付宝扫一扫打赏

博客赞助

微信扫一扫打赏

请作者喝杯咖啡吧~博客赞助

支付宝扫一扫领取红包，优惠每天领

二维码1

领取红包

二维码2

领红包