【Python】scipy稀疏矩阵的奇异值分解svds

这篇具有很好参考价值的文章主要介绍了【Python】scipy稀疏矩阵的奇异值分解svds。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

基本原理

当 $A$ 是方阵时，可以很容易地进行特征分解： $A=W\Sigma W^{-1}$ ，其中 $\Sigma$ 是 $A$ 的特征值组成的对角矩阵。如果 $W$ 由标准正交基组成，则 $W^{-1}=W^T$ ，特征分解可进一步写成 $W^T\Sigma W$ 。

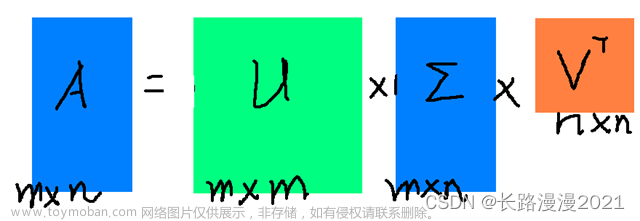
然而，当 $A$ 不是方阵时，情况大不一样了，但仍然可以将 $A$ 表示成 $A=U\Sigma V^T$ 的形式，其中 $\Sigma$ 也是对角矩阵，对角线上的每个元素被称作奇异值。

奇异值的求解过程和特征值息息相关，因为把 $A$ 变成方阵很简单，只要乘以转置就行。故令 $L=AA^T$ ， $R=A^TA$ ，则 $L, R$ 都可以求特征值 $\lambda_i$ 和特征向量，其中 $L$ 的特征向量为 $A$ 的左奇异向量， $R$ 的特征向量为右奇异向量。对应的奇异值 $\sigma_i=\sqrt{\lambda_i}$ 。

scipy实现

scipy.sparse.linalg中实现了稀疏矩阵奇异值分解算法，其参数列表如下

svds(A, k=6, ncv=None, tol=0, which='LM', v0=None, maxiter=None, return_singular_vectors=True, solver='arpack', random_state=None, options=None)

各参数含义如下

A 待分解矩阵
k 奇异值个数，必须在 $k, k_{\max}]$ 之间，当solver='propack'时， $k_{max}=\min(M,N)$ ，否则 $k_{max}=\min(M,N)-1$
ncv solver='arpack'时，此为Lanczos向量个数，否则此项忽略。
tol 奇异值容忍度，为0表示达到机器的精度
which 为'LM'时，选取最大的奇异值；'SM'则选取最小奇异值
v0 迭代初值
maxiter 迭代次数
return_singular_vectors 可选4个值
- True 返回奇异向量
- False 不返回奇异向量
- "u": 如果M <= N，只计算左奇异向量
- "vh": 如果M > N，只计算右奇异向量；如果 solver='propack'，这个选项将忽略矩阵维度
solver 可选'arpack', 'propack', 'lobpcg'，但比较吊诡的是，似乎并没有关于这三者区别的文档
random_state 设置随机数状态
optionsdict 求解器参数

其返回值有三

u 即 $U$
s 即奇异值数组，也就是 $\Sigma$ 的对角线
vh 即 $V^T$

测试

下面对奇异值分解做个测试

import numpy as np
from scipy.linalg import svd
from scipy.sparse import csc_array
from scipy.sparse.linalg import svds
np.random.seed(42)  # 设置随机数状态
mat = np.random.rand(500,800)
mat[mat<0.9] = 0
csc = csc_array(mat)
u1, s1, vh1 = svds(csc, k=10)
u2, s2, vh2 = svd(mat)

结果是svds得到的结果和svd的前十个值完全相同，只是排序不一样，但也无关紧要。

下面测试一下二者的时间，由于在Windows下用不了propack，所以svds计算的奇异值数最多只能是 $M - 1$ ，也就是499，所以只能测试这个和svd返回500个奇异值的结果相比对，结果如下

>>> from timeit import timeit
>>> timeit(lambda : svds(csc, k=499), number=10)
3.651770199999987
>>> timeit(lambda : svd(mat), number=10)
0.47201400000005833