-
-
算法介绍
-
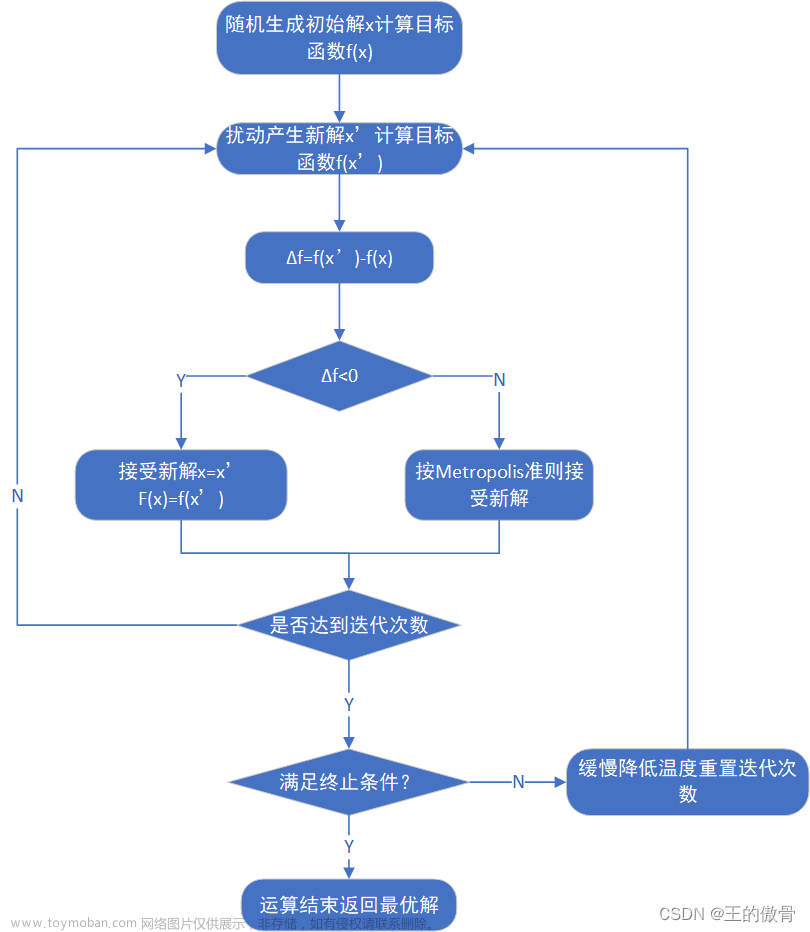
模拟退火算法(SA)是一种模拟物理退火过程而设计的优化算法。
它的基本思想最早在1953年就被Metropolis提出,但直到1983年,Kirkpatrick等人才设计出真正意义上的模拟退火算法并进行应用。
模拟退火算法采用类似于物理退火的过程。先在一个高温状态下,然后逐渐退火,在每个温度下慢慢冷却,最终达到物理基态(相当于算法找到最优解)。
-
-
算法应用
-
求解TSP问题、求最值、全局优化、生产调度、控制工程、机器学习、信号处理等问题。
-
-
算法特性
-
模拟退火算法源于对固体退火过程的模拟,采用Metropolis准则,并用一组称为冷却进度表的参数控制算法的进程,使得算法在多项式时间里可以给出一个近似最优解。
模拟退火算法在某一初温下,伴随温数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解。即在局部最优解的空间内能概率性地跳出并最终趋于全局最优。(不在局限于局部最优)
-
-
算法名词解释
-
退火:将固体加热到足够高的温度,使分子呈随机排列状态,保持足够的时间,然后以适宜的速度逐步降温。使之冷却,最后分子以低能状态排列,固体达到内能最小的稳定状态。(加温—等温—冷却)
-
-
-
退火过程:
-
-
1、在初始状态,固体内部的粒子存在非均匀状态。
2、加热到一定温度,增强其粒子的热运动,使粒子偏离其平衡位置,消除原来的非均匀状态。
3、让温度慢慢降低,达到热平衡状态,粒子逐渐均匀有序,最终达到内能最小的状态。
-
-
算法步骤
-
1.设定当前解(即为当前的最优解):令T=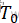 ,即开始退火的初始温度,随机生成一个初始解
,即开始退火的初始温度,随机生成一个初始解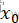 ,并计算相应的目标函数值E(
,并计算相应的目标函数值E(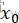 )。
)。
2.产生新解与当前解差值:根据当前解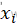 进行扰动,产生一个新解
进行扰动,产生一个新解 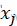 ,计算相应的目标函数值E(
,计算相应的目标函数值E(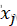 ),得到𝜟𝑬=𝑬(
),得到𝜟𝑬=𝑬(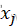 )−𝑬(
)−𝑬(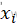 )。
)。
3.判断新解是否被接受:若𝜟𝑬<𝟎,则新解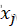 被接受;若𝜟𝑬>𝟎,则新解
被接受;若𝜟𝑬>𝟎,则新解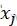 按概率
按概率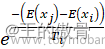 接受,
接受,  为当前温度。
为当前温度。
4.当新解被确定接受时:新解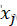 被作为当前解。
被作为当前解。
5.循环以上四个步骤:在温度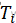 下,重复k次的扰动和接受过程,接着执行下一步骤。
下,重复k次的扰动和接受过程,接着执行下一步骤。
6.最后找到全局最优解:判断T是否已经达到终止温度 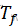 ,是,则终止算法;否,则转到循环步骤继续执行。
,是,则终止算法;否,则转到循环步骤继续执行。
-
-
-
冷却进度表
-
-
退火过程由一组初始参数,即冷却进度表控制。它的目的是尽量使系统达到平衡,以使算法在有限的时间内逼近最优解。
冷却进度表包括:
1.控制温度参数的初值T0
2.控制温度T的衰减函数(温度的更新)
3.马尔科夫链的的长度Lk(迭代次数)
4.控制参数T的终值(停止准则)
| 组合优化问题 |
金属物体 |
| 解 |
粒子状态 |
| 最优解 |
能量最低的状态 |
| 设定初温 |
熔解过程 |
| Metropolis接受过程 |
等温过程 |
| 控制参数的下降 |
冷却 |
| 目标函数 |
能量 |
-
-
模拟退火算法的优缺点
-
优点:
高效地求解NP完全问题(如TSP问题,0-1背包问题等)。
相较于其他非线性与优化算法,模拟退火算法编程工作量小且易于实现。
缺点:
使用不当,可能会陷入局部最优
参数难以控制,所得结果可能为接近最优解但并非最优解。
-
-
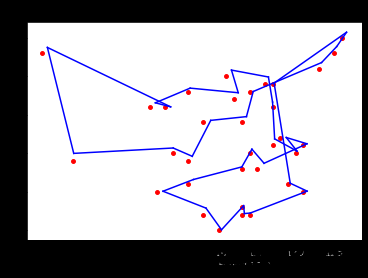
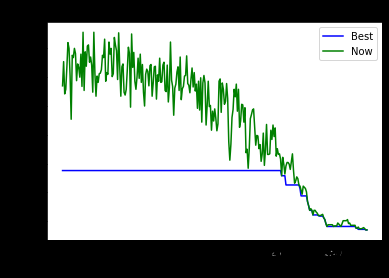
案例1:求解TSP问题
-
问题描述:现有34个城市,已知其坐标;从其中某一城市作为起点出发,途径其他的所有城市,然后回到起点,要求走过的距离最短。

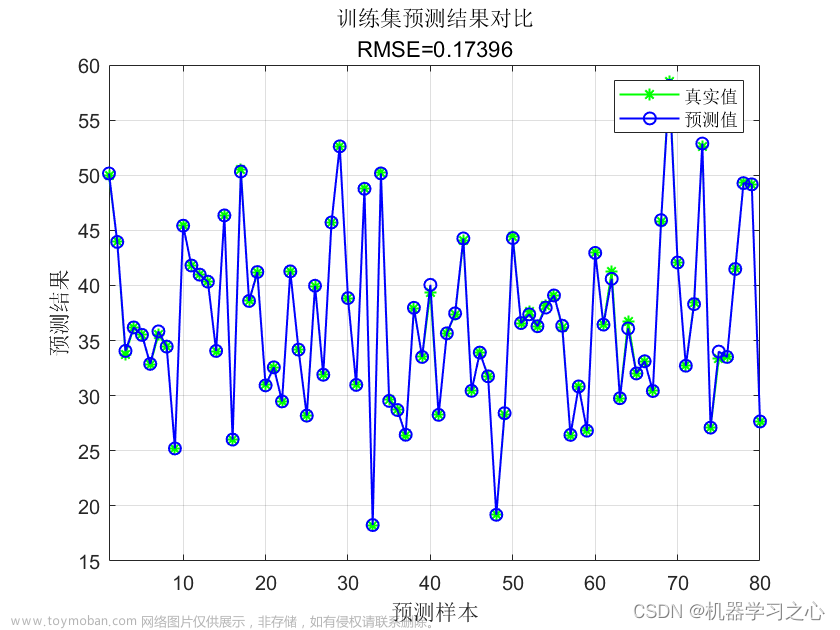
结果如下所示:
 文章来源:https://www.toymoban.com/news/detail-797944.html
文章来源:https://www.toymoban.com/news/detail-797944.html
 文章来源地址https://www.toymoban.com/news/detail-797944.html
文章来源地址https://www.toymoban.com/news/detail-797944.html
到了这里,关于数学建模之模拟退火法(SA)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!