学习目标
- 掌握归并排序的基本原理
- 使用python语言解答归并排序题目
归并排序
原理及过程
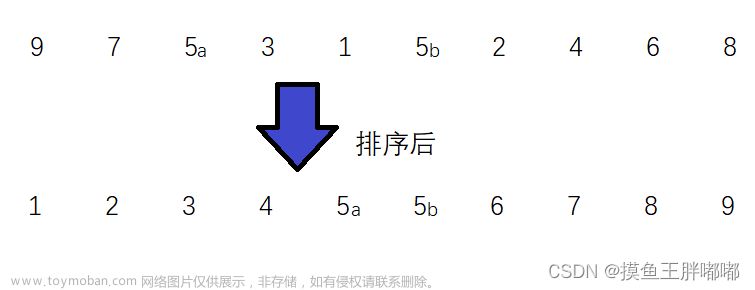
- 将两个有序的数组合并成一个有序数组称为
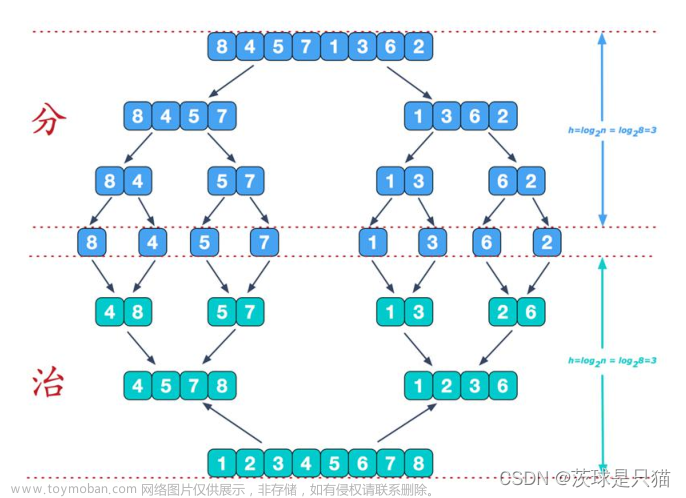
- 从上往下分解:把当前区间一分为二,直至分解为若干个长度为1的子数组
- 从上往下的合并:两个有序的子区域两两向上合并;
- 体现了分治思想,稳定排序
复杂度
平均时间复杂度:O(NlogN)
最坏时间复杂度:O(NlogN)
归并排序合并过程
-
temp数组用于存储合并结果,合并后拷贝回原数组;
-
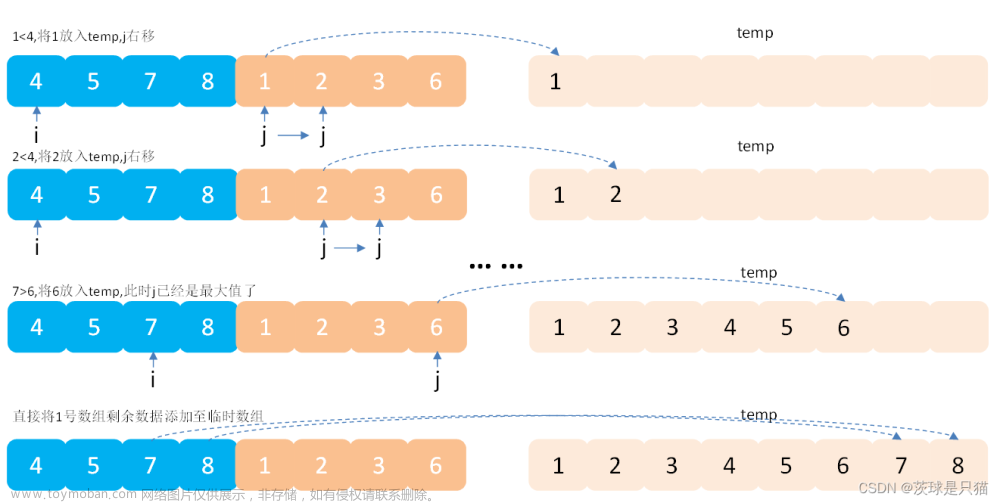
双指针法:
- 初始分别指向两个有序区间的开始位置;
- 指针应该如何移动
-
当合并左右两个有序区间时,分为以下几种情况;
- 左区间、右区间都还有元素,且当前左区间元素值大于右区间元素值;
- 左区间、右区间都还有元素,且当前左区间元素值小于等于右区间元素值;
- 左区间元素值用完、右区间还剩有元素值;
- 右区间元素用完、左区间还剩有元素值。
算法代码实现过程
- 分解:把当前区间一分为二,分解点即中间点mid=(start + end) / 2
- 求解:分别递归左右两个子区间[start… end] 和[mid+1 … end]进行归并排序,递归的终结条件是子区间的长度为1
- 合并:使用双指针法将两个有序区间归并成一个临时有序区间[start … end],并将结果拷贝到原数组的区间[start …end],是原数组[start… end]变为有序。
def merge(nums, start, mid, end):
# 使用双指针法将两个有序区间归并成一个临时有序区间
i, j, temp = start, mid + 1, []
while i <= mid and j <= end:
if nums[i] <= nums[j]:
temp.append(nums[i])
i += 1
else:
temp.append(nums[j])
j += 1
while i <= mid:
temp.append(nums[i])
i += 1
while j <= end:
temp.append(nums[j])
j += 1
for i in range(len(temp)):
nums[start + i] = temp[i]
def mergesort(nums, start, end):
if start >= end:
return
mid = (start + end) >> 1
mergesort(nums, start, mid) # 递归左区间
mergesort(nums, mid + 1, end) # 递归右区间
merge(nums, start, mid, end)
return nums
num_list = [8, 4, 5, 7, 1, 3, 6, 2]
print(mergesort(num_list, 0, len(num_list)- 1))
LCR 170. 交易逆序对的总数
https://leetcode.cn/problems/shu-zu-zhong-de-ni-xu-dui-lcof/description/
解法:归并排序
class Solution:
def reversePairs(self, record: List[int]) -> int:
self.cnt = 0
def merge(nums, start, mid, end):
# 使用双指针法将两个有序区间归并成一个临时有序区间
i, j, temp = start, mid + 1, []
while i <= mid and j <= end:
if nums[i] <= nums[j]:
temp.append(nums[i])
i += 1
else:
self.cnt += mid - i + 1 #更新逆序对的个数
temp.append(nums[j])
j += 1
while i <= mid:
temp.append(nums[i])
i += 1
while j <= end:
temp.append(nums[j])
j += 1
for i in range(len(temp)):
nums[start + i] = temp[i]
def mergesort(nums, start, end):
if start >= end:
return
mid = (start + end) >> 1
mergesort(nums, start, mid) # 递归左区间
mergesort(nums, mid + 1, end) # 递归右区间
merge(nums, start, mid, end)
mergesort(record, 0, len(record) - 1)
return self.cnt
315. 计算右侧小于当前元素的个数(力扣题目)
https://leetcode.cn/problems/count-of-smaller-numbers-after-self/description/
排序+二分解法
-
使用sorted_num数组按照从小到大的顺序存储当前已经遍历过的元素;
-
倒序遍历nums数组中的各个元素n,对于n,完成以下迭代
-
迭代
- 通过二分法找到n在sorted_nums数组中的插入位置index,这个index便是数组sorted_nums中在n右侧且小于n的元素的个数,添加到ans中
- 把n插入到sorted_nums这一有序数组中
-
输出:由于sorted_nums是从右往左添加的,因此最后输出的时候要重新调整回来
class Solution:
def countSmaller(self, nums: List[int]) -> List[int]:
if not nums:
return []
# 按照从小到大的顺序存储当前已经遍历过的所有元素
sorted_num = []
#存储最终结果
ans = []
# 倒序遍历
for n in nums[::-1]:
# 通过二分法找到n在sorted_nums数组中的插入位置index
index = bisect.bisect_left(sorted_num, n)
#把n插入到sorted_nums这一有序数组中
bisect.insort(sorted_num, n)
ans.append(index)
#输出时顺序调整
return ans[::-1]
附录基础
python数据结构与算法理论基础(专栏)
数据结构与算法(python)
程序 = 数据结构 + 算法;而且在面试过程中这些是必考,必问的内容。内容大纲:基础数据结构(树、链表、栈、队列等)、常见算法(排序算法、递归算法等)。
专栏是基于python的基础知识,是很好的入门学习资料。帮助大家快速理解这些数据结构和常见算法的概念,同时结合力扣题目,也能更好的掌握这些知识,达到在面试中游刃有余的效果。
python基础语法
python基础精讲
本专栏主要针对python基础语法,帮助学习者快速接触并掌握python大部分最重要的语法特征。
1、基本数据类型和变量
2、分支结构与循环结构
3、函数与异常处理
4、类与模块
5、文件读写文章来源:https://www.toymoban.com/news/detail-811994.html
通过本专栏可以快速掌握python的基础语法。文章来源地址https://www.toymoban.com/news/detail-811994.html
到了这里,关于python算法与数据结构---排序和归并排序的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!




![[数据结构 -- 手撕排序算法第七篇] 递归实现归并排序](https://imgs.yssmx.com/Uploads/2024/02/573259-1.png)