python算法与数据结构---单调栈与实践-Toy模板网

这篇具有很好参考价值的文章主要介绍了python算法与数据结构---单调栈与实践。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

单调栈

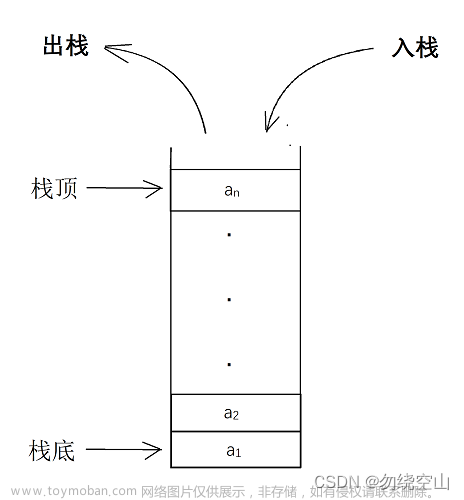
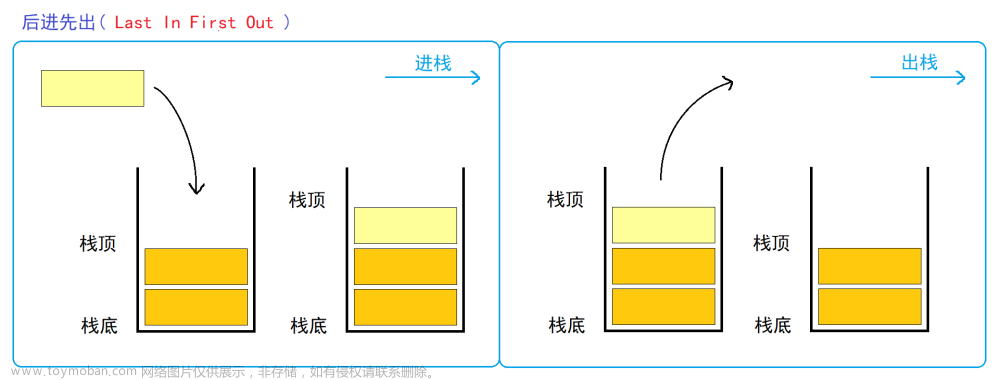
单调栈是一个栈，里面的元素的大小按照它们所在栈的位置，满足一定的单调性；
性质：
- 单调递减栈能找到左边第一个比当前元素大的元素；
- 单调递增栈能找到左边第一个比当前元素小的元素；
应用场景
- 一般用于解决第一个大于XXX或者第一个小于XXX这一类的题目
优点：实践复杂度是线性的，每个元素只遍历一次
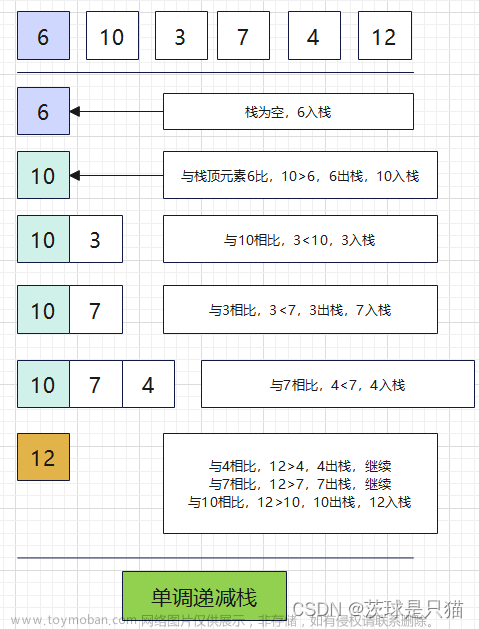
单调递减栈，每次都能找到左边第一个比它大的数
单调递增栈，每次都能找到左边第一个比它小的数

python算法与数据结构---单调栈与实践,python学习及算法数据结构（结合力扣刷题）,python,算法,数据结构

84. 柱状图中最大的矩形

https://leetcode.cn/problems/largest-rectangle-in-histogram/description/
python算法与数据结构---单调栈与实践,python学习及算法数据结构（结合力扣刷题）,python,算法,数据结构

解法一：暴力解法

依次遍历柱形的高度，对于每一个高度分别向两边扩散，求出当前高度为矩形的最大宽度

向左遍历，看最多能向左延伸多长，找到大于等于当前柱形高度的最左边元素的下标；
向右遍历，看最多能向右延伸多长，找到大于等于当前柱形高度的最右边元素的下标；
计算当前高度对应的最大面积，与历史最大值进行比较并更新。

该解法在用例数量过多时，容易超出实时间限制

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        size = len(heights)
        res = 0
        for i in range(size):
            # 找左边最后一个大于等于heights[i]的下标
            left = i
            cur_height = heights[i]
            while left > 0 and heights[left-1] >= cur_height:
                left -= 1
            
            # 找右边最后一个大于等于heights[i]的下标
            right = i
            while right < size-1 and heights[right + 1] >= cur_height:
                right += 1
            
            max_width = right - left + 1
            res = max(res, max_width * cur_height)
        return res

解法二：单调栈

获取每根柱子左边第一个比它低的柱子坐标，（单调递增栈）
获取每根柱子右边第一个比它低的柱子下标，（倒序来做，就是左边第一个比它低的柱子）
遍历每根柱子求最大面积
哨兵技巧：两边各添加一个虚拟柱子

class Solution:
    def largestRectangleArea(self, heights: List[int]) -> int:
        stack = []
        left = [0 for _ in range(len(heights))]
        right = [0 for _ in range(len(heights))]
        res = 0

        # 获取每根柱子左边第一个比它低的柱子下标
        for i in range(len(heights)):
            while stack and heights[stack[-1]] >= heights[i]:
                stack.pop()
            if not stack:
                left[i] = -1
            else:
                left[i] = stack[-1]
            stack.append(i)

        stack = []
        # 获取每根柱子右边第一个比它低的柱子下标
        for j in range(len(heights) - 1, -1, -1):
            while stack and heights[stack[-1]] >= heights[j]:
                stack.pop()
            if not stack:
                right[j] = len(heights)
            else:
                right[j] = stack[-1]
            stack.append(j)
        
        # 求最大面积
        for i in range(len(heights)):
            res = max(res, heights[i] * (right[i] - left[i] - 1))
        
        return res