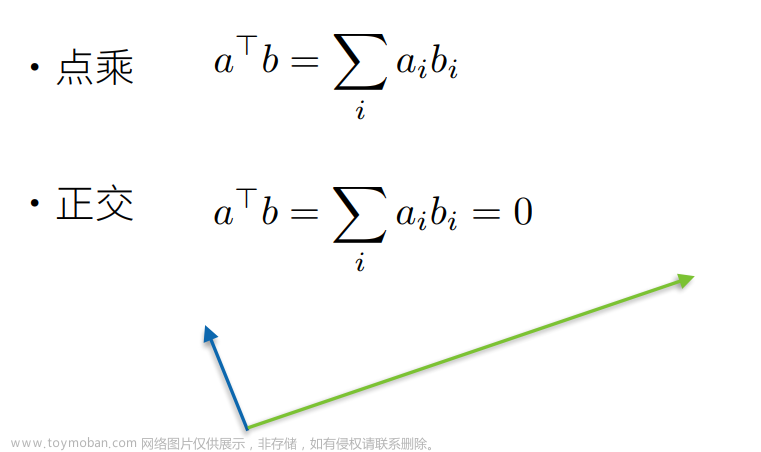
概述
在实际应用中,数据通常以表的形式出现。尽管用数组来描述表是最自然的方式,但为了减少程序所需的时间和空间,经常采用自定义的描述方式。例如,当表中大部分数据为 0的时候,就会用自定义的描述方式。
本章首先检查了多维数组的行主描述方式和列主描述方式。这些描述方式把多维数组映射成一维数组。
矩阵经常用二维数组来描述。然而,矩阵的索引通常从 1 开始,而 C++ 的二维数组是从0 开始。矩阵的操作有加法、乘法和转置,但是 C++ 的二维数组不支持这些操作。因此我们开发了类 matrix. 它与矩阵的关系更密切。
我们还要考察具有特殊结构的矩阵,如对角矩阵、三对角矩阵、三角矩阵和对称矩阵。关于这些矩阵的描述方法,自定义数组与二维数组相比,不仅大大减少了存储空间,也减少了大多数矩阵操作的运行时间。
本章的最后一节设计了稀疏矩阵(即大部分元素为 0 的矩阵)的数组和链表描述方式,对 0 元素做了特殊的处理
7.1 数组
7.1.1 抽象数据类型
一个数组的每一个实例都是形如(索引,值)的数对集合,其中任意两个数对的索引( index )都不相同。
有关数组的操作如下:
- 取值一一 一对一个给定的索引,取对应数对中的值。
- 存值一一把一个新数对加到数对集合中。如果已存在一个索引相同的数对,就用新数对覆盖。
7.1.2 C++数组的索引
略了,太简单。
7.1.3 行主映射和列主映射
数组的应用需要我们把数组元素序列化,即按一维顺序排列。
说的就是高维数组变成一维数组。
然后说到映射二维数组:行主和列主。
对应由不同的公式,直接略了。
然后扩展到更多维度,思路一样,略。
7.1.4 用数组的数组描述
C++ 用所谓数组的数组来表示一个多维数组。一个二维数组被表示为一个一维数组,这个一维数组的每一个元素还是一个一维数组。
7.1.5 行主描述和列主描述
这是C++没有的表示方法,创建一个一维数组,然后利用行主/列主映射,把多维数组映射到这个一维数组。
C++ 数组中是行主描述法快还是列主描述法快,这取决于是先用一维映射函数定位指针,再用指针定位元素的方法快,还是用二维映射函数定位元素的方法快
7.1.6 不规则二维数组
规则的二维数组指每行元素个数相同的二维数组。当一个二维数组有两行以上,它们的元素个数不相等时,该数组称为不规则数组。
//一个不规则二维数组的创建和使用
int main(void)
{
int numberOfRows = 5;
//定义每一行的长度
int length[5] = [6,3,4,2,7];
//声明一个二维数组变量
//且分配所需要的行数
int **irregularArray = new int* [numberOfRows];
//分配每一行的空间
for (int i=0;i<numberOfRows;i++)
irregularArray[i] = new int [length[i]];
//像使用规则数组一样使用不规则数组
irregularArray[2][3] = 5;
irregularArray]4][6]= irregularArray[2][3] + 2;
irregularArray[1][1] = 3;
//输出略
return 0;
}
这里就是一个指针的指针的数组,然后每一行单独分配空间。
7.2 矩阵
7.2.1 定义和操作
线性代数学过,略了。
7.2.2 类matrix
用二维整数数组表示矩阵。
//类matrix的声明
template<class T>
class matrix
{
friend ostream& operator<<(pstream&, const metrix<T>&);
public:
matrix(int theRows = 0, int theColumns = 0);
matrix(const matrix<T>&);
~matrix() {delete [] element;}
int rows() const {return theRows;}
int columns() const {return theColumns;}
T& operator()(int i, int j) const;
matrix<T>& operator=(const matrix<T>&);
matrix<T> operator+() const; //unary +
matrix<T> operator+(const matrix<T>&) const;
matrix<T> operator-() const; //unary +
matrix<T> operator-(const matrix<T>&) const;
matrix<T> operator*(const matrix<T>&) const;
matrix<T> operator+=(const T&);
private:
int theRows; //矩阵的行数
int theColumns; //矩阵的列数
T *element; //数组element
};
// 构造函数和复制构造函数
template<class T>
matrix<T>::matrix(int theRows, the Columns)
{
//矩阵构造函数
//检验行数和列数的有效性
if (theRows < 0 || theColumns < 0)
throw illegalParameterValue("Rows and columns must be >= 0");
if ((theRows == 0 || theColumns == 0) && (theRows!=0||theColumns!=0))
throw illegalParameterValue("Either both or neither rows and columns should be zero");
//创建矩阵
this->theRows = theRows;
this->theColumns = theColumns;
element = new T [theRows * theColumns];
}
template<class T>
matrix<T>::matrix(const matrix<T>& m)
{
//矩阵的复制构造函数
//创建矩阵
theRows = m.theRows;
theColumns = m.theColumns;
element = new T [theRows*theColumns];
//复制m的每一个元素
copy(m.element,m.element + theRows * theColumns, element);
}
//对赋值操作符=的重载
template<class T>
matrix<T>& matrix<T>::operator=(const matrix<T>& m)
{
//赋值 . (*this) = m
if(this != &m)
{
//不能自己复制自己
delete [] element;
theRows = m.theRows;
theColumns = m.theColumns;
element = new T [theRows * theColumns];
//复制每一个元素
copy(m.element,m.element + theRows * theColumns, element);
}
return *this;
}
//对()操作符的重载
template<class T>
T& matrix<T>::operator()(int i, int j) const
{
//返回对元素element(i,j)的引用
if(i<1||i>theRows||j<1||j>theColumns)
throw matrixIndexOutOfBounds();
return element[(i-1)*theColumns + j - 1];
}
//对+操作符重载
template<class T>
matrix<T> matrix<T>::operator+(const matrix<T>& m) const
{
//返回矩阵 w = (*this)+m;
if(theRows!=m.theRows||theColumns!=m.theColumns)
throw matrixSizeMismatch();
//生成结果矩阵
matrix<T> w(theRows,theColumns);
for(int i=0;i<theRows*theColumns;i++)
w.element[i] = element[i]+m.element[i];
return 2;
}
//矩阵乘法
template<class T>
matrix<T> matrix<T>::operator*(const matrix<T>& m) const
{
//矩阵乘法 , 返回结果矩阵w = (*this) * m
if(theColumns!=m.theRows)
throw matrixSizeMismatch();
//生成结果矩阵
matrix<T> w(theRows,m.theColumns);
//定义矩阵 *this, m和w 的游标且初始化以为(1,1)元素定位
int ct = 0, cm = 0, cw = 0;
//对所有i和j计算 w(i,j)
for (int i = 1; i <= theRows; i++)
{
//计算结果矩阵的第i行
for(int j = 1;j<m.theColumns; j++)
{
//计算w(i,j)第一项
T sum = element[ct] * m.element[cm];
//累加其余所有项
for (int k = 2; k <= theColumns; k++)
{
ct++; //*this中的第i行的下一项
cm += m.theColumns; //m中第j列的下一项
sum += element[ct] * m.element[cm];
}
w.element[cw++] = sum; //存储在w(i,j)
//从行的起点和下一列从新开始
ct -= theColumns - 1;
cm = j;
}
//从下一行和第一列重新开始
ct += theColumns;
cm = 0;
}
return w;
}
7.3 特殊矩阵
7.3.1 定义和应用
7.3.2 对角矩阵
//声明和构造函数
template<class T>
class diagonalMatrix
{
public:
diagonalMatrix(int theN = 10);
~diagonalMatrix() (delete [] element;)
T get(int, int) const;
void set(int, int, const T&);
private:
int n; //矩阵维数
T *element; //存储对角矩阵的一维数组
}
template<class T>
diagonalMatrix<T>::diagonalMatrix(int theN)
{
//构造函数
//检验theN的值是否有效
if (theN < 1)
throw illegalParameterValue("Matrix size must be > 0");
n = theN;
element = new T [n];
}
//方法get
template<class T>
T diagonalmatrix<T>::get(int i, int j) const
{
//返回矩阵中(i,j)位置上的元素
//检验i和j的值是否有效
if(i<1||i>theRows||j<1||j>theColumns)
throw matrixIndexOutOfBounds();
if(i == j)
return element[i-1]; //对角线上的元素
else
return 0; //非对角线上的元素
}
//方法set
template<class T>
void diagnoalMatrix<T>::set(int i, int j, const T& newValue)
{
//检验i和j的值是否有效
if(i<1||i>theRows||j<1||j>theColumns)
throw matrixIndexOutOfBounds();
if(i == j)
//存储对角元素的值
element[i-1]=newValue;
else
//非对角必须是0
if(newValue !=0)
throw illegalParameterValue
("nondiagonal elements must be zero");
}
7.3.3 三对角矩阵
//方法get
template<class T>
T tridiagonalmatrix<T>::get(int i, int j) const
{//返回矩阵中(i,j)位置上的元素
//检验i和j的值是否有效
if(i<1||i>theRows||j<1||j>theColumns)
throw matrixIndexOutOfBounds();
//确定要返回的元素
switch(i-j)
{
case 1://下对角线
return element[i - 2];
case 2://主对角线
return element[n+i-2];
case 3://上对角线
return element[2 * n + i - 2];
default: return 0;
}
}
7.3.4 三角矩阵
template<class T>
void lowerTriangularMatrix<T>::set(int i, int j, const T& newValue)
{
//给(i,j)元素赋新值
//检验i和j的值是否合法
if(i<1||i>theRows||j<1||j>theColumns)
throw matrixIndexOutOfBounds();
if(i >= j)
element[i * (i-1) / 2 + j - 1] = newValue;
else
if (newValue != 0)
throw illegalParameterValue
("elements not in lower triangle must be zero");
}
7.3.5对角矩阵
一个n x n对称矩阵,可以视为下三角或上三角矩阵,用三角矩阵的表示方法,用一个大小为n(n+1)/2 的一维数组来表示。未存储的元素可以用存储的元素来计算。
7.4 稀疏矩阵
7.4.1 基本概念
一个m x n 的矩阵,如果大多数元素都是0,则称为稀疏矩阵。一个矩阵如果不是稀疏的,就称为稠密矩阵。二者之间并没有明确的界限。
本节规定,稀疏矩阵的非0元素要小于n2/3,甚至n2/5。
7.4.2 用单个线性表描述
按行主次序,把无规则稀疏矩阵映射到一个线性表中。
为了重建矩阵结构,必须记录每个非0元素的行号和列号,因此需要三个域:row(所在行)、col(所在列)和value(矩阵元素的值)。
定义结构体:3个数据成员,整型row和col,T类型value。
稀疏矩阵这种描述方法节省了初始化二维数组的时间。
但是没有提高get和set的执行效率:
- 折半查找get执行时间O(log[非0元素个数])
- set时间是O(非零元素个数)
- 采用链表,两个函数都是O(非零元素个数)
- 二维数组,都是O(1)。
- 不过使用线性表,诸如转置、加法和乘法都可以提高效率
1.类 sparseMatrix
//类sparseMatrix的头
template<class T>
class sparseMatrix
{
public:
void transpose<sparseMatrix<T> &b);
void add(sparseMatrix<T> &b, sparseMatrix<T> &c);
private:
int rows, //矩阵行数
cols; //矩阵列数
arrayList<matrixTerm<T> > terms; //非0项表
};
//重载<<。注意,这个代码对类arrayList的元素使用了从左至右的舒徐迭代器,行主顺序提取非0元素,一行输出一个矩阵项。
template<class T>
ostream& operator<<(ostream& out,sparseMatrix<T>& x)
{
//将x放入输出流
//输出矩阵特征
out << "rows = " << x.rows << " columns = " << x.cols << endl;
out << "onozero terms = " << x.terms.size() << endl;
//输出矩阵项,一行一个
for (arrayList<matrixTerm<T> >::iterator i = x.terms.begin();
i != x.terms.end(); i++)
out << "a(" << (*i).rows << ',' << (*i).col
<< ") = " << (*i).value << endl;
return out;
}
//重载>>
template<class T>
ostream& operator>>(istream& in,sparseMatrix<T>& x)
{
//输入一个稀疏矩阵
//输入矩阵特征
int numberOfTerms;
cout << "Enter number of rows, columns, and #terms"<< endl;
int >> x.rows >> x.cols >> numberOfTerms;
//这里检查输入合理性
//设置x.terms的大小,确保足够的容量
x.terms.reSet(numberOfTerms);
//输入项
matrixTerm<T> mTerm;
for (int i = 0; i < numberOfTerms; i++)
{
cout << "Enter row, column, and value of term "
<< (i + 1) << endl;
in >> mTerm.row >> mTerm.col >> mTerm.value;
//这里应该检验输入合理性
x.terms.set(i, mTerm);
}
return in;
}
2. 矩阵转置
// 稀疏矩阵的转置
template<class T>
void sparseMatrix<T>::transpose(sparseMatrix<T> &b)
{
//返回b中*this的转置
//设置转置矩阵特征
b.cols = rows;
b.rows = cols;
b.terms.reSet(terms.size());
//初始化以实现转置
int* colSize = new int[cols + 1];
int* rowNext = new int[cols + 1];
//寻找*this 中每一项的数目
for(int i = 1; i <= cols; i++) //初始化
colSize[i] = 0;
for (arrayList<matrixTerm<T> >::iterator i = terms.begin());
i != terms.end(); i++)
colSize[(*i).col]++;
//寻找b中每一行的起始点
rowNext[1] = 0;
for (int i = 2; i <= cols; i++)
rowNext[i] = rowNext[i - 1] + colSize[i - 1];
//实施从*this到b的转置复制
matrixTerm<T> mTerm;
for (arrayList<matrixTerm<T> >::iterator i = terms.begin());
i != terms.end(); i++)
{
int j = rowNext[(*i).col]++; //b中的位置
mTerm.row = (*i).col;
mTerm.col = (*i).row;
mTerm.value = (*i).value;
b.terms.set(j, mTerm);
}
}
3. 两个矩阵相加
template<class T>
void sparseMatrix<T>::add(sparseMatrix<T> &b, sparseMatrix<T> &c)
{
//计算c = (*this) + b
//检验相容性
if (rows != b.rows || cols != b.cols)
throw matrixSizeMismatch(); //矩阵不相容
//设置结果矩阵c的特征
c.rows = rows;
c.cols = cols;
c.terms.clear();
int cSize = 0;
//定义*this和b的迭代器
arrayList<matrixTerm<T> >::iterator it = terms.begin();
arrayList<matrixTerm<T> >::iterator ib = b.terms.begin();
arrayList<matrixTerm<T> >::iterator itEnd = terms.end();
arrayList<matrixTerm<T> >::iterator inEnd = b.terms.end();
//遍历*this和b,把相关的项相加
while (it != itEnd && ib != ibEnd)
{
//行主索引加上每一列的列数
int tIndex = (*it).row * cols + (*it).col;
int bIndex = (*ib).row * cols + (*ib).col;
if (tIndex < bIndex)
{
//b项在后
c.terms.insert(cSize++, *it);
it++;
}
else {if (tIndex == bIndex)
{//两项在同一个位置
//仅当相加后不为0时加入c
if((*it).value + (*ib).value != 0)
{
matrixTerm<T> mTerm;
mTerm.row = (*it).row;
mTerm.col = (*it).col;
mTerm.value = (*it).value + (*ib).value;
c.terms.insert(cSize++, mTerm);
}
it++;
ib++;
}
else
{//一项在后
c.terms.insert(cSize++, *ib);
ib++;
}
}
}
//复制剩余项
for (; it != itEnd; it++)
c.terms.insert(cSize++, *it);
for (; ib != ibEnd; ib++)
c.terms.insert(cSize++, *ib);
}
7.4.3 用多个线性表描述
把每一行的非0元素用一个线性表存储,就得到描述稀疏矩阵的另一种方法。这里使用链表。
1.表示方法
把每行的非0元素串在一起,构成一个行链表。
一行至少有一个非0元素,才会建立该行的行链表。所有行链表被另一个链表(头结点链表)收集在一起。
2.链表元素类型
结构 rowElement 定义了行链表的元素类型。它的数据成员有 col (元素的行索引)和value(元素的值)。结构 headerElement 定义了头节点链表的元素类型。它的数据域有 row (行索引)和 rowChain(实际的链表,数据类型是 extendedChain)。
3.类linkedMatrix
略了,即把前面内容转化为类
4.转置方法linkedMatrix<T>::transpose
这里的代码先略,后期有时间再补。文章来源:https://www.toymoban.com/news/detail-845050.html
7.4.4 性能测量
linkedMatrix 方法虽然比 sparseMatrtix 方法慢,但是比 2DArray 方法快。 sparseM atrix 方法与 2DArray 方法比,时间减少的程度是显著的,矩阵加法和转置的时间大约为后者的 1 / 20 。文章来源地址https://www.toymoban.com/news/detail-845050.html
到了这里,关于第7章 数组和矩阵的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!