前段时间我导给我提出了一个任务,让我提取出离散点的外围边界点。作为技术小白的我,在网上狂搜资料。也走了很多弯路,最终根据Delaunay的三角形的特点(即所有三角形边中,只存在一个三角形中的边即为轮廓边,包含的点即为轮廓点。)来完成。
csdn上也有很多写得很好的博客,我就用自己的想法同时参考《Delaunay 三角网生长算法改进与实现》这篇文章来叙述三角网生长算法的构建过程及原理。同时结合python/C++代码,让大家更好的实现Tin!
闲话少说,TIN三角网的用途博主不再强调,此篇博客主要用于实现三角网!!!
三角网原理
三角网生长法的基本算法思路是:首先找到所有离散点中相距最短的两点,将其连接作为首三角形的初始边(基边)。然后,按照D-TIN判断法找到包含此边的Delaunay三角形的第三点,连接此点与初始边的两个顶点构成首三角形;再按D-TIN判断法以首三角形中另外两条边为基线,分别搜索第三点构成另外两条边的Delaunay三角形,依次循环,直至所有离散点均成为D-TIN的端点。
构网步骤
现假定待构网的离散点的个数为n,下面对三角网生长法的基本步骤进行简单介绍与实现分析:
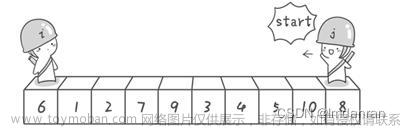
第一步:在包含n离散点的点集中寻找任意两个点之间的距离最小的点对,将此两点连接起来作为初始基线。
第二步:找首三角形。应用Delaunay判断法在初始基线的右边搜索第三点。D-TIN判断法的具体方法是以基线的两个端点作为向量的起点,依次将其余的未构网的n-2个点作为向量的终点,利用公式(下图)计算两个向量间夹角的余弦值。其中P1和P2分别为基线的两个端点,Pi为还未参与构网的其他点。在这所有的余弦值中,找余弦值最小的点作为首三角形的第三点。
第三步:以三角形的三条边为基线,寻找与基线构成三角形的可能的扩展点。一条基线最多是两个三角形的公共边,因此,当基线在寻找可能扩展点的时候,应保证扩展点与基线已构成的三角形的第三点分别位于基线的两侧。否则可能会导致三角形的重叠。以下图(1)的三角形为例,寻找基线T1T2的可能扩展点判断方法如下:
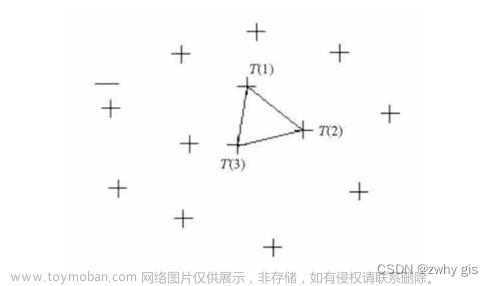
首先给出基线T(1)T(2)的直线方程,记T1(x1, y1), T2(x2, y2),利用向量的叉乘计算基线的函数方程,直线上任一点(x, y)有:
在这里我们可以对未构网的离散点P(x, y)及上图 中T(3)点分别代入直线方程中,并判断f (x, y)的符号,给定以下约定:

若f(p)与f(T(3))同号(即同为正区域或负区域),则P点不是可能扩展点;若f(p)与f(T(3))异号,则P点是可能的扩展点。
第四步:对于可能的扩展点判断是否满足Delaunay原则。此步骤类似于寻找首三角形的第三点,即在所有可扩展点中寻找余弦值最小的点且构成的边不能为重复扩展边。
第五步:重复第三、第四步直到所有点都连线完毕,则构网结束。
C++分步代码
前期准备:需要定义三个类,分别为点类(Point)、线类(Line)、向量类(MyVector)。一个结构体(LineInfo)
# include <iostream>
# include <math.h>
# include <random>
# include <vector>
# include <fstream>
# include <string>
# include <ctime>class Point {
public:
double x, y, z;
//默认构造函数
Point(){};
//构造函数
Point(double x, double y, double z=0) {
this -> x = x;
this -> y = y;
this -> z = z;
}
//计算两点间的距离
double cal_distence(Point& other) {
double distence = 0.0;
distence = pow(pow(this->x - other.x, 2) + pow(this->y - other.y, 2), 0.5);
return distence;
}
//重写==
bool operator == (const Point& p) {
bool b1 = this->x == p.x;
bool b2 = this->y == p.y;
bool b3 = this->z == p.z;
if (b1 and b2 and b3) {
return true;
}
return false;
}
};class Line {
public:
//sametinpt为同一个三角形的顶点(类似原理中的T(3))
Point startpt, endpt, sametinpt;
//flag用于判断该边被使用了几次(一个三角形最多只能作为两个三角形的边)
int flag;
//构造函数
Line() {};
Line(Point& p1, Point& p2, Point& p3, int flag = 0) {
this->startpt = p1;
this->endpt = p2;
this->flag = flag;
this->sametinpt = p3;
}
//重写==
bool operator == (const Line& l) {
bool b1 = this->startpt == l.startpt;
bool b2 = this->endpt == l.endpt;
bool b11 = this->startpt == l.endpt;
bool b22 = this->endpt == l.startpt;
if ((b1 and b2) or (b11 and b22)) {
return true;
}
return false;
}
};class MyVector {
public:
Point startpt, endpt;
//length为向量的长度
double xx, yy, zz, length;
//构造函数
MyVector() {
}
MyVector(Point& sp, Point& ep) {
this->startpt = sp;
this->endpt = ep;
this->xx = ep.x - sp.x;
this->yy = ep.y - sp.y;
this->zz = ep.z - sp.z;
this->length = pow(pow(this->xx, 2) + pow(this->yy, 2) + pow(this->zz, 2), 0.5);
}
//两向量间的叉乘
double cal_vector(const MyVector& v1) {
return this->xx * v1.yy - this->yy * v1.xx;
}
//两向量间的点乘
double cal_number(const MyVector& v1) {
return this->xx * v1.xx + this->yy * v1.yy + this->zz * v1.zz;
}
};//结构体,用于存储不同类型的值
struct LineInfo
{
//count为判断边的已使用次数
int count;
// index为判断边位于列表中的位置
int index;
};定义三个全局vector变量ptlist(存储所有点)、allline(存储所有边)、baseline(存储所有基线边)
//ptlist用于存储所有点
vector<Point> ptlist;
//allline用于存储所有三角形边
vector<Line> allline;
//baseline用于存储基线边
vector<Line> baseline;利用random头文件随机生成离散点,用于实验下面:
//随机生成点
void generaterand(int num) {
default_random_engine e;
uniform_real_distribution<double> u(0.0, 10);
e.seed(time(0));
for (int i = 0; i < num; i++) {
ptlist.push_back(Point(u(e), u(e)));
}
}将离散点中最近的两点找出返回,并在点集中删除这两点
Point* findcloestpt(std::vector<Point>& v) {
// 静态变量可以返回
static Point cp[2];
// 初始化
Point p1 = v[0];
Point p2 = v[1];
int index1 = 0;
int index2 = 1;
double mindis = p1.cal_distence(p2);
//寻找出最近的两个点
for (int i = 1; i < v.size() - 1;i++) {
for (int j = i + 1; j < v.size(); j++) {
double tempdis = v[i].cal_distence(v[j]);
if (mindis > tempdis) {
p1 = v[i];
p2 = v[j];
index1 = i;
index2 = j;
mindis = tempdis;
}
}
}
cp[0] = p1;
cp[1] = p2;
// 将两点从点列表中删除
v.erase(v.begin() + index1);
// 注意!!!!这里-1是因为上面已经删了一个点,所有它的索引随之减小了一个
v.erase(v.begin() + index2-1);
cout << "最短距离为:" << mindis << endl;
return cp;
}根据余弦定理公式 ,分别与剩余点计算,找出最小的余弦值的点,组成第一个三角形。
void findfirsttin(Point& p1, Point& p2, std::vector<Point>& v) {
// 初始化
MyVector mv1, mv2;
int index = 0;
mv1 = MyVector(p1, v[0]);
mv2 = MyVector(p2, v[0]);
double cos00 = mv1.cal_number(mv2) / (mv1.length * mv2.length);
// 循环找出最小的余弦值
for (int i = 1; i < v.size(); i++) {
mv1 = MyVector(p1, v[i]);
mv2 = MyVector(p2, v[i]);
double cos0 = mv1.cal_number(mv2) / (mv1.length * mv2.length);
if (cos0 < cos00) {
cos00 = cos0;
index = i;
}
}
// 形成三条边,同时存入allline和baseline
Line line1 = Line(p1, p2, ptlist[index], 1);
Line line2 = Line(p1, ptlist[index], p2, 1);
Line line3 = Line(p2, ptlist[index], p1, 1);
allline = { line1, line2, line3 };
baseline = { line1, line2, line3 };
cout << "第一个三角形已经寻找成功" << endl;
cout << "三角形总边数为:" << allline.size() << endl;
}我们在进行下面的建网过程会碰到一个问题,就是如何判断这个边它在整个三角形网中的使用次数?很简单的,我们利用前文Line类中的flag属性即可;具体判断函数代码如下:
struct LineInfo lineusedcount(Line& line, std::vector<Line>& v) {
// 结构体用于返回信息
LineInfo lineinfo;
// 与allline中每条边判断
for (int i = 0; i < v.size(); i++) {
// 我们已在Line类中重写了==
if (line == v[i]) {
// 如果该边已经使用了两次,即已经存在于两三角形中
if (v[i].flag == 2) {
lineinfo.count = 2;
lineinfo.index = i;
return lineinfo;
}
// 如果该边只存在于一个三角形内
else
{
lineinfo.count = 1;
lineinfo.index = i;
return lineinfo;
}
}
}
// 如果这条边是新边,即allline表中没有它
lineinfo.count = 0;
lineinfo.index = -1;
return lineinfo;
}构网
void creatTin(std::vector<Line>& va, std::vector<Line>& vb,std::vector<Point>& vp) {
//建网结束的标志就是基线表baseline不存在元素了
while (vb.size())
{
// 依次对基线表中的基线进行扩展
Line baseline = vb[0];
// 如果该基线虽然还没有扩展,但是其它基线边扩展的过程中已经产生了它2次,那它将不会进行扩展
// 因为一条边 最多 存在于两个三角形内
if (lineusedcount(baseline, va).count==2) {
vb.erase(vb.begin());
continue;
}
// 寻找第三点
while (true)
{
// potential用于存储可能的扩展点
std::vector<Point> potentialpt;
double re1 = MyVector(baseline.startpt, baseline.endpt).cal_vector(MyVector(baseline.startpt, baseline.sametinpt));
for (int i = 0; i < vp.size(); i++) {
double re2 = MyVector(baseline.startpt, baseline.endpt).cal_vector(MyVector(baseline.startpt, vp[i]));
// 异号才可能是扩展边
if (re1 * re2 < 0) {
potentialpt.push_back(vp[i]);
}
}
// 如果列表为0。及该基线可能为最外层的边,它的一边不存在点了
if (potentialpt.size() == 0) {
vb.erase(vb.begin());
break;
}
// 找出最小的余弦值
MyVector mv1, mv2;
int index=0;
mv1 = MyVector(baseline.startpt, potentialpt[0]);
mv2 = MyVector(baseline.endpt, potentialpt[0]);
double cos00 = mv1.cal_number(mv2) / (mv1.length * mv2.length);
for (int i = 1; i < potentialpt.size(); i++) {
mv1 = MyVector(baseline.startpt, potentialpt[i]);
mv2 = MyVector(baseline.endpt, potentialpt[i]);
double cos0 = mv1.cal_number(mv2) / (mv1.length * mv2.length);
if (cos0 < cos00) {
cos00 = cos0;
index = i;
}
}
// 组成可能的扩展边
Line newl1 = Line(baseline.startpt, potentialpt[index], baseline.endpt, 1);
Line newl2 = Line(baseline.endpt, potentialpt[index], baseline.startpt, 1);
LineInfo info1 = lineusedcount(newl1, va);
// 如果是“新出现”的边,同时加入allline和baseline
if (info1.count == 0) {
va.push_back(newl1);
vb.push_back(newl1);
}
// 否则将其flag的值改为2
else
{
vb.push_back(newl1);
va[info1.index].flag = 2;
}
LineInfo info2 = lineusedcount(newl2, va);
if (info2.count == 0) {
va.push_back(newl2);
vb.push_back(newl2);
}
else
{
vb.push_back(newl2);
va[info2.index].flag = 2;
}
// 基线边只要经过一次扩展,肯定存在于两三角形内
va[lineusedcount(baseline, va).index].flag = 2;
vb.erase(vb.begin());
break;
}
//cout << vb.size() << endl;
}
cout << "构网结束!" << endl;
}主函数main
int main(){
generaterand(1000);
cout << "列表个数为:" << ptlist.size() << std::endl;
fstream file;
file.open("H:\\points.txt", ios::out);
for (int i = 0; i < ptlist.size(); i++) {
file << to_string(ptlist[i].x) << "," << to_string(ptlist[i].y) << "\n";
}
file.close();
cout << "原始点存储成功" << endl;
/*vector<int> a = { 1,2,3,4,5 };
a.erase(a.begin() + 2);
for (int i = 0; i < a.size(); i++) {
cout << a[i] << endl;
}*/
Point *ccpp;
double st = clock();
ccpp = findcloestpt(ptlist);
cout << "列表个数为:" << ptlist.size() << std::endl;
cout << "相邻两点第一个点的坐标为:" << ccpp->x <<","<< ccpp->y << endl;
cout << "相邻两点第二个点的坐标为:" << (ccpp+1)->x << ","<<(ccpp + 1)->y << endl;
findfirsttin(*ccpp, *(ccpp + 1), ptlist);
creatTin(allline, baseline, ptlist);
cout << "构网用时:" << clock() - st << "ms" << endl;
cout << "三角形总边数为:" << allline.size() << endl;
return 0;
}构建的三角网
 文章来源:https://www.toymoban.com/news/detail-861773.html
文章来源:https://www.toymoban.com/news/detail-861773.html
此章结束,博主叙述难免会有遗漏或疏忽,大家如果有啥疑惑可以留言沟通。同时如果需要python版本的程序,我会近期出一期相关博客! 文章来源地址https://www.toymoban.com/news/detail-861773.html
到了这里,关于三角网(TIN)生成算法的原理及实现(有代码!!!)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!