动态规划之使用最小花费爬楼梯-Toy模板网

这篇具有很好参考价值的文章主要介绍了动态规划之使用最小花费爬楼梯。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

1. 题目分析

题目链接选自力扣 : 使用最小花费爬楼梯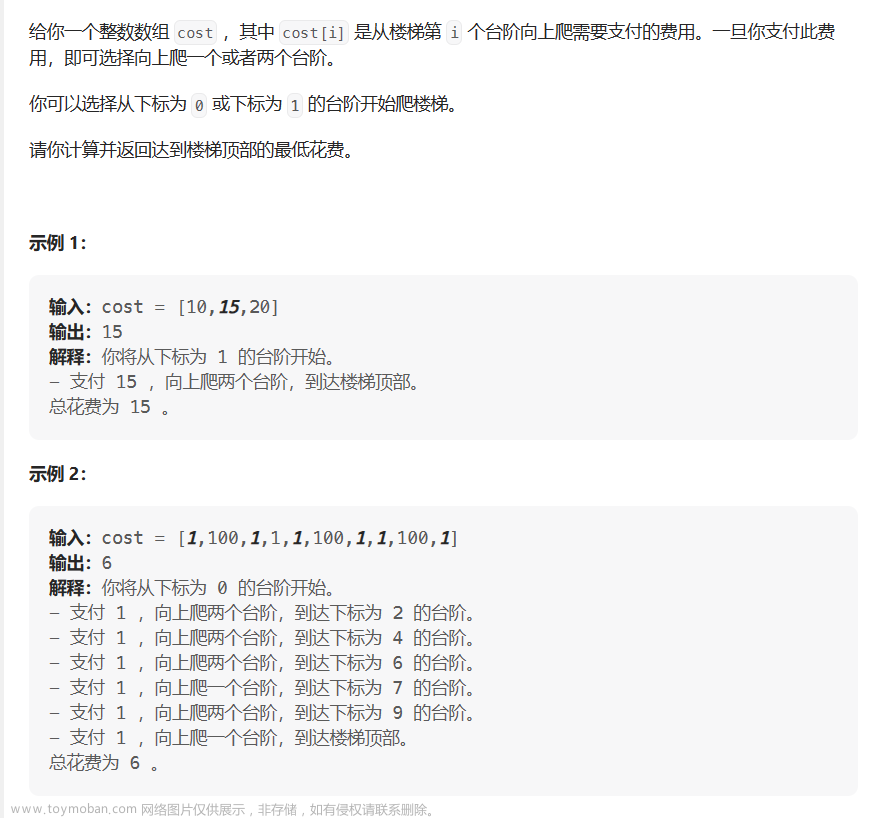

先根据示例 1 来理解一下题目的意思.

可以看到, 此时一共有两个起始位置 0 ,1. 并且这三个位置都对应了一定的费用 10, 15 当我们选择从某个地方开始想要向上走就得支付当前位置的费用才可以向上一格或者两格.

当前这个示例就是从 1 位置处, 支付 15元, 并且一次走两步就到达了楼顶, 最终花费 15元.

为什么说是楼梯顶部在 2 位置下一处呢 ? 原因很简单, 如果在 2 位置处. 我选择从 0 位置支付 10 元直接跳一次两步到 2 位置处支付的费用最少为 10元. 但是用例给的是最低费用为 15元. 因此 3 下标处才是楼梯顶部.

这就意味着, 即使到达了数组的最后位置, 也需要支付当前这个位置的费用才可以到达楼顶.

再来看看示例 2, 肯定是从 0 位置起始此时最便宜. 花 1 元选择从 0 位置开始后, 下一次有 1, 2 位置可以选, 此时选 2 位置最便宜. 接着花费 1 元从 2 位置开始有 3, 4 位置可以选. 两者费用一致下选择到 4 位置, 依次类推… 当到达 9 位置的时候, 此时已经花了 5元了, 但是还没有到达楼顶, 还需要支付 1 元向上一步到达楼顶. 因此一共是 6 元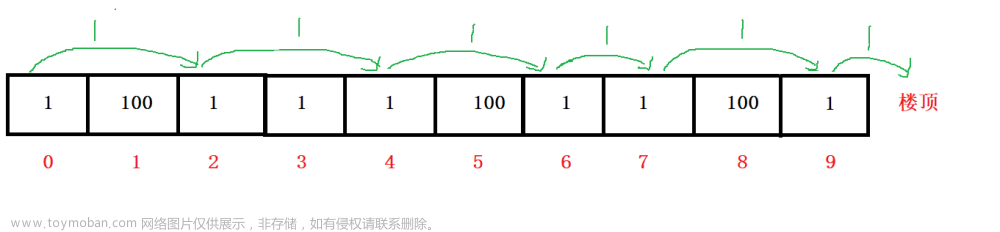

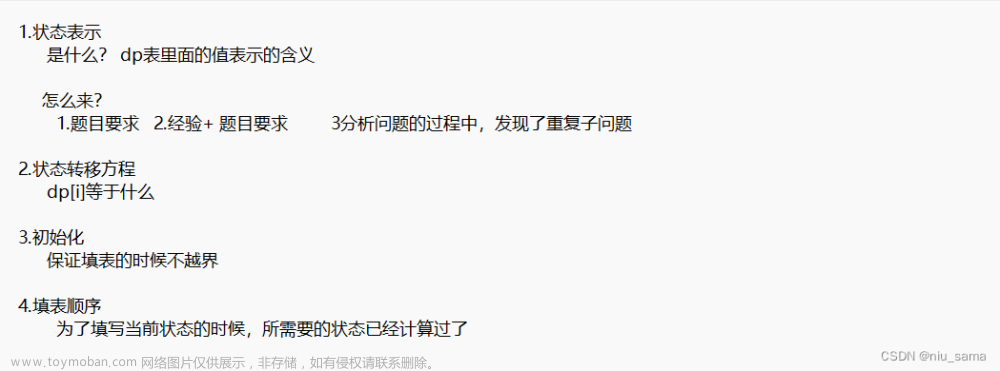
2. 状态表示

以 i 位置为结尾. 表示从第 0 或 1 位置开始到达 i 后最终上到楼顶所需要的花费
定义一个一维数组 int dp[] = new int[n + 1], 其中 dp[i] 即表示从 0 或 1 位置开始到达 i 位置后上顶楼所花费的最小值

3. 状态转移方程

根据我们前面的三步问题还有 N 哥泰波那契数所积攒的经验, 此时的状态方程可以根据最近的一步来划分问题.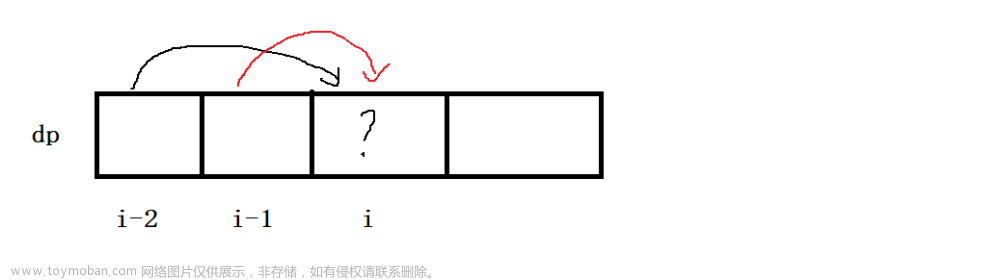

可以看到, 当我们相求 dp[i] 也就是第 i 个位置时的最小花费, 它有两种可能

一种是从 i - 2 处花费对应钱走 2 步到达 i 位置

此时我们可以看这时候的话费为多少呢 ? 也就是到达 dp[i - 2] 位置时的花费在加上 cost[i - 2] ( 也就是到达 i 位置后还需要话费当前位置的钱走一步到楼顶 )

另一种为 i - 1 处花费对应钱走 1 步到达 i 位置

此时我们可以看到这时候话费为 dp[i - 1] + cost[i - 1]

我们最终要计算的 dp[i] 有这两种方案, 那么那种最省钱 dp[i] 就是那种对应方案. 因此动态转移方为 :
dp[i] = Math.Min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2] )

4. 初始化

初始化就是为了防止 dp 数组越界. 当我们想要计算 dp[1] 时就必须要知道 dp[0] 和 dp[-1] 以及 cost[0] 和 cost[-1] 的值. 显然这是越界了的. 需要我们单独进行处理.

从题目可以知道 dp[0] = 0, dp[1] = 0. 因为可以直接从 0 或 1 位置开始, 到达这两个位置并不需要花费

5. 填表顺序

想要知道 dp[i] 就需要先知道前面的 dp[i - 1] 和 dp[i - 2] 因此顺序是从左往右填表

6. 返回值

题目要求返回从 0 或 1 位置开始向上爬到 n 后上楼顶的最低花费, 因此返回值为 dp[n]

7. 代码演示

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;


        // 1. 创建 dp 表
        int[] dp = new int[n + 1];


        // 2. 初始化
        dp[0] = dp[1] = 0;


        // 3. 填写 dp 表
        for(int i = 2; i <= n; i++) {
            dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
        }
        // 4. 确定返回值
        return dp[n];
    }
}

8. 第二种解法

8.1 状态表示

除了上面的这种状态表示, 还有另一种状态表示. 即以 i 位置为起点, 到达楼顶的最小花费.

并且从 i 位置到楼 n 后, 并不在需要支付 n 位置的费用. 此时已经在楼顶了. 因此 dp 数组的大小为 dp[n]

8.2 状态方程

此时的状态转移方程就变成了以下情况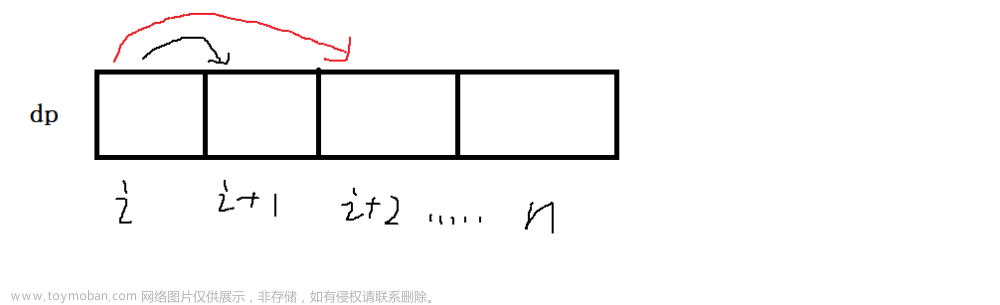

当支付了 cost[i] 的费用后, 选择走 1 步到 i + 1 位置, 然后从该位置出发到达楼顶

此时的费用为 cost[i] 加上从 i + 1 位置时的花费. 根据我们的转态表示. i + 1 位置的花费正好就是表示从 i + 1 位置开始到楼顶的最小花费. 因此为 dp[i+1]

当支付了 cost[i] 的费用后, 选择走 2 步到 i + 2 位置, 然后从该位置出发到达楼顶

同理, 此时的费用为 cost[i] + dp[i+2]
选择两种方法中的最小花费.
因此状态转移方程为 : dp[i] = Math.min(cost[i] + dp[i+1], cost[i] + dp[i+2])

8.3 初始化

根据状态转移方程, 当楼顶为 n 时, 我们需要知道最后两个位置到达楼顶的最小花费. 因此需要初始化这两个位置的值. 而最后这两个位置要到达楼顶, 只需要支付当前自身费用即可向上 1 步或者 2 步到达楼顶. 因此 dp[n-1] = cost[n - 1], dp[n - 2] = cost[n - 2]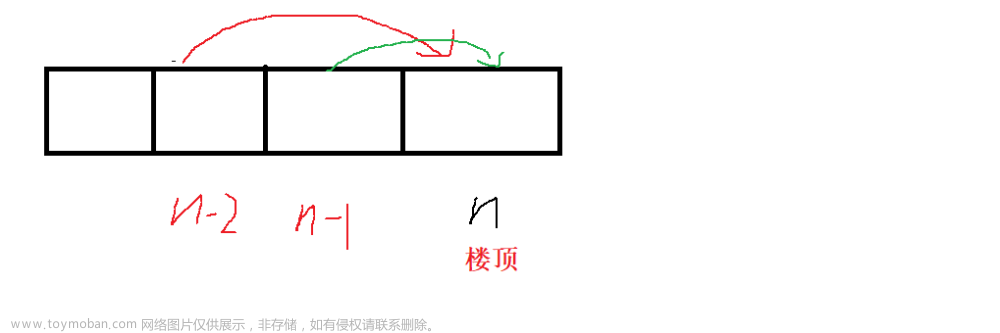

8.4 填表顺序

当要知道 dp[i] 位置到达楼顶的最小花费时, 需要先计算出dp[i + 1] 和 dp[i + 2] 位置的值. 因此是从右向左填写. 也就是从 dp 表的后面向前填写.

8.5 返回值

我们是从 i 位置开始到达楼顶的最小费用. 但题目给的是只能从 0 或 1 位置开始. 因此当我们从后向前填写了 dp 表后, 每一个位置的值都是该位置到达 n 点的最小花费. 因此填写到 dp[0] 以及dp[1] 时也是从该点到 n 点楼顶的最小花费. 因此返回值为 Math.Min(dp[0], dp[1])文章来源地址https://www.toymoban.com/news/detail-497180.html

8.6 代码演示

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int n = cost.length;
        
        // 1. 创建 dp 表
        int[] dp = new int[n];

        // 2. 初始化
        dp[n - 1] = cost[n - 1];
        dp[n - 2] = cost[n - 2];

        // 3. 填写 dp 表
        for(int i = n - 3; i >= 0; i--) {
            dp[i] =  Math.min(cost[i] + dp[i+1], cost[i] + dp[i+2]);
        }

        // 4. 确认返回值
        return Math.min(dp[0], dp[1]);
    }
}