信息增益-决策树

这篇具有很好参考价值的文章主要介绍了信息增益-决策树。希望对大家有所帮助。如果存在错误或未考虑完全的地方，请大家不吝赐教，您也可以点击"举报违法"按钮提交疑问。

信息增益-决策树,决策树,算法,机器学习
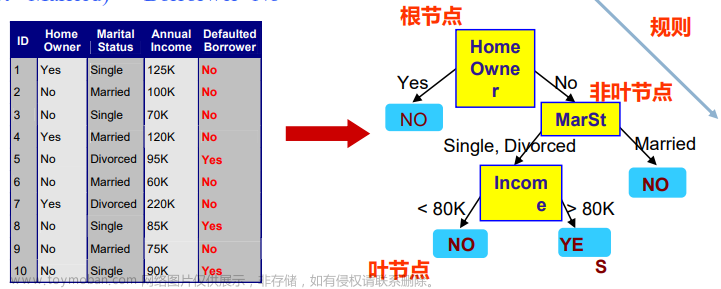
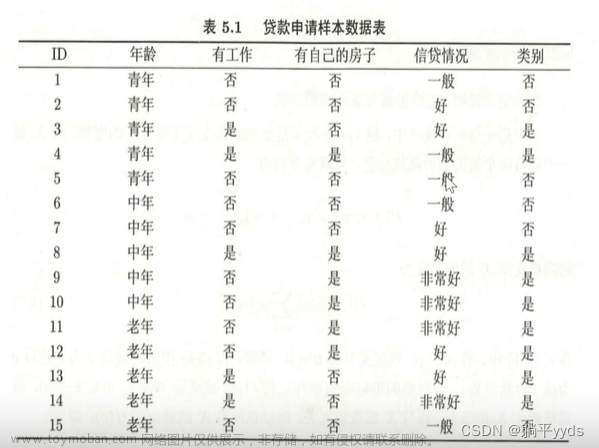
表8.1给出的是带有标记类的元组的训练集D；

类标号属性 buys_computer有两个不同值：{yes, no}

设类 C1 $\rightarrow$ yes，C2 $\rightarrow$ no;

已知：C1包含9个元组，C2包含5个元组；

信息增益-决策树,决策树,算法,机器学习

age：{‘youth’, ‘middle_aged’, ‘senior’}

	youth	middle_aged	senior
yes	2	4	3
no	3	0	2

信息增益-决策树,决策树,算法,机器学习

对于 $yo u t h$ 来说：
$D_{j}$ = $2 + 3 = 5$
$I n f o$ ( $D_{j}$ ) = - $2/5$ * $log_{2}$ ( $2/5$ ) - $3/5$ * $log_{2}$ ( $3/5$ )

即，

信息增益-决策树,决策树,算法,机器学习

即，按年龄划分的信息增益：
$G ain (a g e) = I n f o (D)$ - $Info_{age}(D)$ = 0.94-0.694 = 0.246

同理，
$G ain (in co m e) = 0.029$ ， $G ain (s t u d e n t) = 0.151$ ，
$G ain (cre d i t$ _ $r a t in g) = 0.048$

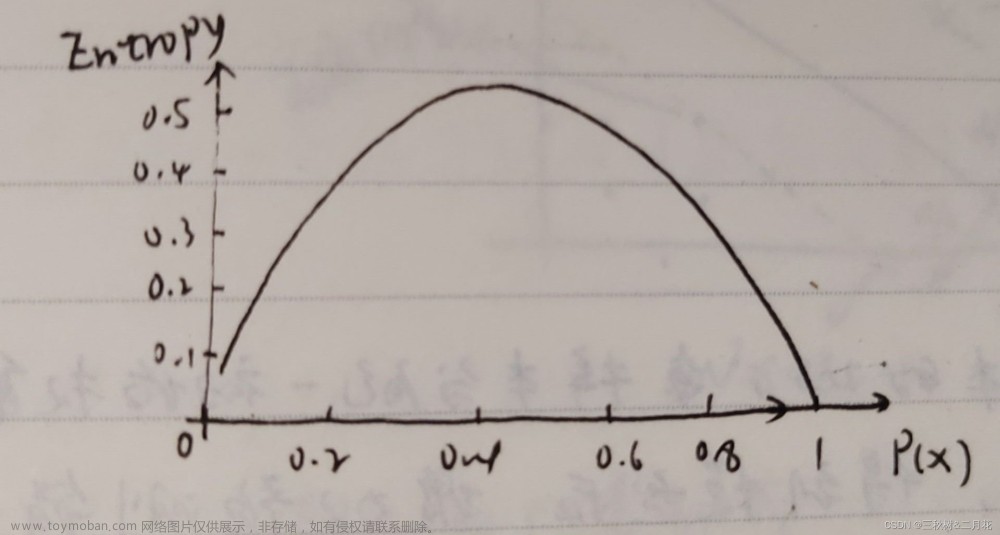
信息熵：意思是一个变量的变化情况可能越多，那么它携带的信息量就越大，信息熵值越大，该系统越不稳定，存在的不定因素就越多。

信息熵的增益是指：所有属性值的信息熵和某一个属性值的信息熵的差值，增益值越大，说明其具有更高的决策性，可做为优先节点。

由于age在属性中具有最高的信息增益，所以它被选作分裂属性；

由于age $\rightarrow$ middle_aged 元组属于相同的类，所以在该分支的端点创建一个树叶，并用 yes 标记；

最终决策树如下：
信息增益-决策树,决策树,算法,机器学习

参考：文章来源地址https://www.toymoban.com/news/detail-841335.html

到了这里，关于信息增益-决策树的文章就介绍完了。如果您还想了解更多内容，请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章，希望大家以后多多支持TOY模板网！

Toy模板网