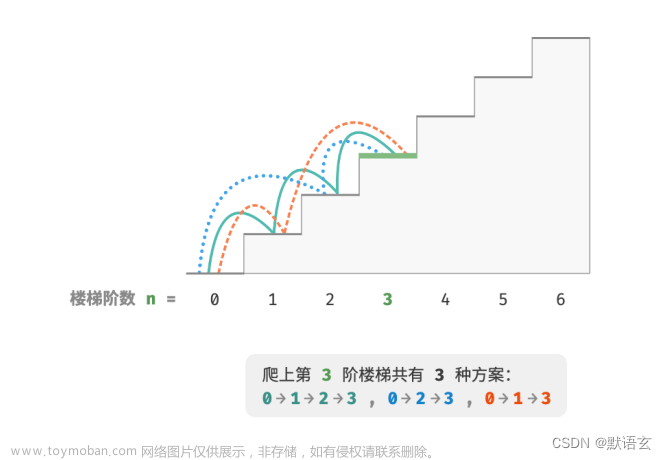
这篇文章主要讲两种基础的背包问题01背包和完全背包,其实主要是作者太菜。
01背包问题
首先来看一下问题描述
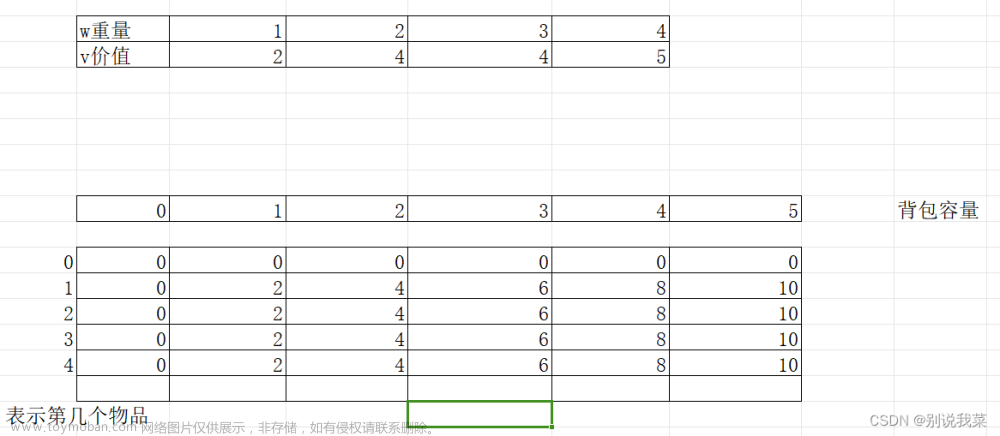
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
此处给出一个示例

基本步骤
1.确定缓存数组dp和其索引的含义
行对应着往背包装入的物品,列对应着背包的最大容量
注意物品是有限的,每个物品只有一个行对应着可以往背包装入的物品编号(0-i中的物品编号都可以取),列对应着背包的最大容量,二维数组的值表示在该情况下物品的最大价值。
2.确定递推公式
在确定递推公式时,我们一定要找一个示例自己推一遍。
我们容易想到在二维数组中有两种情况:一个是在当前能用的物品(行)和对应容量情况(列)下有能装得下的方案,另一个是在当前能用的物品(行)和对应容量情况(列)下没有能装得下的方案。
比较列索引j(容量)和物品对象数组items[i](i为行索引)看在当前的容量下是否能装入新物品。
装不下:此时使价值最大的方案与上一行同列的元素一致,因此直接把二维数组上一行同列的元素赋值给当前元素。
装得下:需要比较一下上一行在相同容量下的最大价值和现在放入了新物品后的最大价值,取价值最大的情况。那该如何获得放入了新物品后的最大价值呢?我们可以取上一行同列的元素,用列索引减去新物品的重量得到一个新的二维数组值,该值表示如果装入了新物品那么剩下的空间对应的最大价值。我们把新物品的最大价值加上该新的二维数组的值便得到放入了新物品后的最大价值。那为什么不用同行的元素的列索引减新物品的重量呢?由于物品是只有一个的,如果用同行的元素的列索引减新物品的重量,那么得到的剩余容量所对应的最大价值方案中是有可能重复装入了新物品的,这就与题目条件中说的每一件物品只有一个不符了。这也是01背包问题和任意背包问题的区别。
伪代码
if(装不下) {
dp[i][j] = dp[i-1][j]
} else { 装得下
dp[i][j] = max(dp[i-1][j], item.value + dp[i-1][j-item.weight])
}
3.数组初始化
数组如何初始化主要是看递推公式。
1.如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
2.从dp[i][j] = max(dp[i-1][j], item.value + dp[i-1][j-item.weight]可以看出i 是由 i-1 推导出来,那么i为0的时候就一定要初始化。
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
初始化代码如下
Item item0 = items[0];
for (int j = 0; j < total + 1; j++) {
if (j >= item0.weight) { // 装得下
dp[0][j] = item0.value;
} else { // 装不下
dp[0][j] = 0;
}
}4.dp数组遍历赋值
先遍历物品还是先遍历背包容量其实都可以,我这里选择先遍历物品,这样更好理解:在可以放入这些索引(0-i)对应的物品情况下,二维数数组的值表示不同容量下的最大价值。
for (int i=1;i<dp.length;i++){
Item item=items[i];
for (int j=0;j<total+1;j++){
int x=dp[i-1][j];
if (j>item.weight){
dp[i][j]=Integer.max(x,dp[i-1][j-item.weight]+item.value);
}
else {
dp[i][j]=x;
}
}
}具体代码如下
package algorithm.dynamicProgramming;
import java.util.Arrays;
import java.util.stream.IntStream;
/**
* 背包问题-动态规划
* @author CSDN编程小猹
* @date 2023/11/07
*/
public class KnapsackProblem {
static class Item {
int index;
String name;
int weight;
int value;
public Item(int index, String name, int weight, int value) {
this.index = index;
this.name = name;
this.weight = weight;
this.value = value;
}
@Override
public String toString() {
return "Item(" + name + ")";
}
}
public static void main(String[] args) {
Item[] items = new Item[]{
new Item(1, "黄金", 4, 1600),
new Item(2, "宝石", 8, 2400),
new Item(3, "白银", 5, 30),
new Item(4, "钻石", 1, 10_000),
};
System.out.println(select(items, 10));
}
private static int select(Item[] items, int total) {
int[][] dp = new int[items.length][total + 1];
//第零行不符合递推公式,需要特殊处理
Item item0 = items[0];
for (int j = 0; j < total + 1; j++) {
if (j >= item0.weight) { // 装得下
dp[0][j] = item0.value;
} else { // 装不下
dp[0][j] = 0;
}
}
print(dp);//调试打印
for (int i=1;i<dp.length;i++){
Item item=items[i];
for (int j=0;j<total+1;j++){
int x=dp[i-1][j];
if (j>item.weight){
dp[i][j]=Integer.max(x,dp[i-1][j-item.weight]+item.value);
}
else {
dp[i][j]=x;
}
}
}
print(dp);
return dp[dp.length-1][total];
}
static void print(int[][] dp) {
System.out.println(" " + "-".repeat(63));
Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
System.out.printf(("%5d ".repeat(dp[0].length)) + "%n", array);
for (int[] d : dp) {
array = Arrays.stream(d).boxed().toArray();
System.out.printf(("%5d ".repeat(d.length)) + "%n", array);
}
}
}
算法优化
算法的主要优化方向是:缓存数组可以进行压缩,降维成一维数组。
我们观察递推公式dp[i][j]=Integer.max(x,dp[i-1][j-item.weight]+item.value)可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是dp[j] = Integer.max(dp[j], item.value + dp[j - item.weight])我们完全可以不需要一个二维数组来缓存结果,我们从递推式中可以看出一行的元素只与上一行的元素有关,而二维数组则将每一行的元素都存储了下来,浪费了空间。我们只需要一个一维数组对结果进行缓存,每次更新元素时便可用dp[j] = Integer.max(dp[j], item.value + dp[j - item.weight])来递推。
分析步骤的话依然按照上面的来
1.确定缓存数组dp和其索引的含义
在一维dp数组中,dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]
2.确定递推公式
dp[j]为 容量为j的背包所背的最大价值,那么如何推导dp[j]呢?
dp[j]可以通过dp[j - weight[i]]推导出来,dp[j - weight[i]]表示容量为j - weight[i]的背包所背的最大价值。
dp[j - weight[i]] + value[i] 表示 容量为 j - 物品i重量 的背包 加上 物品i的价值。(也就是容量为j的背包,放入物品i了之后的价值即:dp[j])
此时dp[j]有两个选择,一个是外层循环到了一个寻物品items[i]后,如果背包不能装下则取自己dp[j] 相当于 二维dp数组中的dp[i-1][j],即不放items[i],一个是取dp[j - weight[i]] + value[i],即可以放入items[i],两种情况的价值进行比较取最大值。
伪代码
if(装不下) {
dp[j] = dp[j]
} else { 装得下
dp[j] = max(dp[j], item.value + dp[j-item.weight])
}
3.dp数组初始化
关于初始化,一定要和dp数组的定义吻合,否则到递推公式的时候就会越来越乱。
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
那么dp数组除了下标0的位置,初始为0,其他下标应该初始化多少呢?
看一下递归公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
dp数组在推导的时候一定是取价值最大的数,如果题目给的价值都是正整数那么非0下标都初始化为0就可以了。
这样才能让dp数组在递归公式的过程中取的最大的价值,而不是被初始值覆盖了。
那么我假设物品价值都是大于0的,所以dp数组初始化的时候,都初始为0就可以了。
4.dp数组遍历赋值
这里大家发现和二维dp的写法中,遍历背包的顺序是不一样的!
二维dp遍历的时候,背包容量是从小到大,而一维dp遍历的时候,背包是从大到小。
为什么呢?
倒序遍历是为了保证物品i只被放入一次。但如果一旦正序遍历了,那么物品0就会被重复加入多次!(此处与01背包问题和完全背包问题递推式不同的原理是一样的)
举一个例子:0物品的重量items[0].weight= 4,0物品的价值items.value[0] = 1600
如果正序遍历
dp[4] = dp[4 - items[0].weight] + items[0].value = 1600
dp[8] = dp[8 - items[0].weight] + items[0].value = 3200
此时dp[8]就已经是30了,意味着物品0,被放入了两次,所以不能正序遍历。
为什么倒序遍历,就可以保证物品只放入一次呢?
倒序就是先算dp[8]
dp[8] = dp[8 - items[0].weight] + items[0].value = 1600(dp数组已经都初始化为0)
dp[4] = dp[4 - items[0].weight] + items[0].value = 1600
所以从后往前循环,每次取得状态不会和之前取得状态重合,这样每种物品就只取一次了。
那为什么二维dp数组遍历的时候不用倒序呢?
我们观察递推式dp[i][j]=Integer.max(x,dp[i-1][j-item.weight]+item.value)可以看出对于二维dp,放入了新物品后的剩余背包容量最大值dp[i][j]都是通过上一层即dp[i - 1][j]计算而来,不会存在物品被重复放入的情况!
再来看看两个嵌套for循环的顺序,代码中是先遍历物品嵌套遍历背包容量,那可不可以先遍历背包容量嵌套遍历物品呢?
不可以!
因为一维dp的写法,背包容量一定是要倒序遍历(原因上面已经讲了),如果遍历背包容量放在上一层,那么每个dp[j]就只会放入一个物品,即:背包里只放入了一个物品。倒序遍历的原因是,本质上还是一个对二维数组的遍历,并且右下角的值依赖上一层左上角的值,因此需要保证左边的值仍然是上一层的,从右向左覆盖。
所以一维dp数组的背包在遍历顺序上和二维其实是有很大差异的!,如果这里看得有点迷糊可以自己动手去调试一下。
下面是优化后的算法代码
//算法优化:数组降维
static int select2(Item[] items, int total) {
int[] dp = new int[total + 1];
for (Item item : items) {
//注意此处要逆序
for (int j = total; j > 0; j--) {
if (j >= item.weight) { // 装得下
dp[j] = Integer.max(dp[j], item.value + dp[j - item.weight]);
}
}
System.out.println(Arrays.toString(dp));
}
return dp[total];
}完全背包问题
问题描述
有N种物品和一个最多能背重量为W的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品都有无限个(也就是可以放入背包多次),求解将哪些物品装入背包里物品价值总和最大。
此处给出一个示例

分析
由于完全背包问题和01背包问题只有一些细小的差别,此处就不按照上面的步骤一步步写了
与01背包问题不同的是每个要放入的物品都是无限个的
首先看一下01背包的递推公式:
优化前
for (int i=1;i<dp.length;i++){ Item item=items[i]; for (int j=0;j<total+1;j++){ int x=dp[i-1][j]; if (j>item.weight){ dp[i][j]=Integer.max(x,dp[i-1][j-item.weight]+item.value); } else { dp[i][j]=x; } } }优化后
for (Item item : items) { //注意此处要逆序 for (int j = total; j > 0; j--) { if (j >= item.weight) { // 装得下 dp[j] = Integer.max(dp[j], item.value + dp[j - item.weight]); } } System.out.println(Arrays.toString(dp)); }完全背包问题的递推公式
由于完全背包问题中的一类物品是可以无限放入的,因此在装得下的情况下dp[i][j]=Integer.max(dp[i-1][j],dp[i][j-item.weight]+item.value),此时的背包在装下新物品后的剩余容量最大价值的取值不再是从上一行取得,因为新物品可以重复放入,因此剩余容量最大价值的取值可以从同一行取。
优化前:
for (int j=0;j<total+1;j++){ //装得下 Item item=items[i]; int x=dp[i-1][j];//上次的最大价值 if (j>=item.weight){ dp[i][j]=Integer.max(x,dp[i][j-item.weight]+item.value); } else { dp[i][j]=x; } }我们知道01背包内层循环是从大到小遍历,为了保证每个物品仅被添加一次。
而完全背包的物品是可以添加多次的,所以要从小到大去遍历
优化后:
for (int j = 0; j < total + 1; j++) { if (j >= item.weight) { dp[j]= Integer.max(dp[j], dp[j - item.weight] + item.value); } }
具体代码如下:
import java.util.Arrays;
import java.util.function.ToLongBiFunction;
import java.util.stream.IntStream;
/**
* 完全背包问题
* @author CSDN编程小猹
* @date 2023/11/07
*/
public class KnapsackProblemComplete {
static class Item {
int index;
String name;
int weight;
int value;
public Item(int index, String name, int weight, int value) {
this.index = index;
this.name = name;
this.weight = weight;
this.value = value;
}
@Override
public String toString() {
return "Item(" + name + ")";
}
}
static void print(int[][] dp) {
System.out.println(" " + "-".repeat(63));
Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
System.out.printf(("%5d ".repeat(dp[0].length)) + "%n", array);
for (int[] d : dp) {
array = Arrays.stream(d).boxed().toArray();
System.out.printf(("%5d ".repeat(d.length)) + "%n", array);
}
}
public static void main(String[] args) {
Item[] items = new Item[]{
new Item(1, "青铜", 2, 3), // c
new Item(2, "白银", 3, 4), // s
new Item(3, "黄金", 4, 7), // a
};
System.out.println(select(items, 6));
}
private static int select(Item[] items, int total) {
int [][]dp=new int[items.length][total+1];
Item item0=items[0];
//第零行不符合递推式,需要另外赋值
for (int j=0;j<total+1;j++){
//装得下
if (j>=item0.weight){
dp[0][j]=dp[0][j-item0.weight]+item0.value;
}
}
print(dp);
for (int i=1;i<items.length;i++){
for (int j=0;j<total+1;j++){
//装得下
Item item=items[i];
int x=dp[i-1][j];//上次的最大价值
if (j>=item.weight){
dp[i][j]=Integer.max(x,dp[i][j-item.weight]+item.value);
}
else {
dp[i][j]=x;
}
}
}
print(dp);
return dp[items.length-1][total];
}
//优化:把缓存结果的数组降维
private static int select2(Item[] items, int total) {
int[] dp = new int[total + 1];
for (Item item : items) {
for (int j = 0; j < total + 1; j++) {
if (j >= item.weight) {
dp[j]= Integer.max(dp[j], dp[j - item.weight] + item.value);
}
}
System.out.println(Arrays.toString(dp));
}
return dp[total];
}
}
练习推荐
找了一些题目进行练习
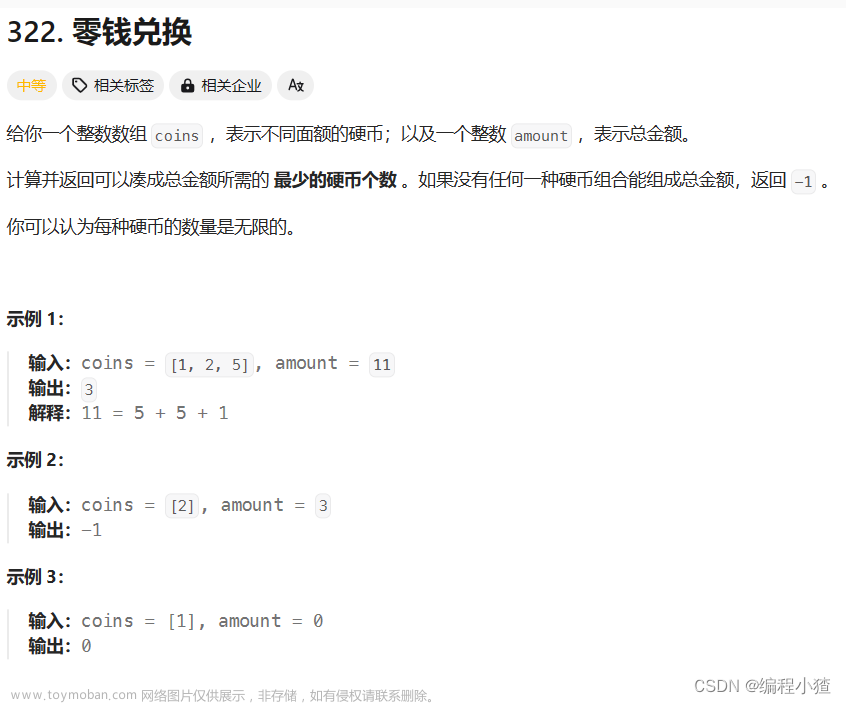
322.零钱兑换

基本步骤
1.确定缓存数组dp和其索引的含义
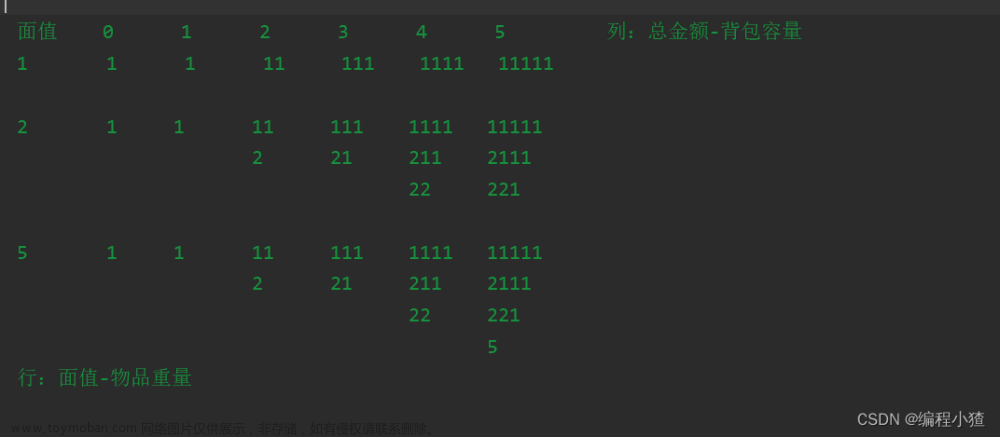
行(i)代表不同硬币的面额,列(j)代表总金额,二维数组的值dp[i][j]代表着在0-i个不同硬币面值和总金额数为j的情况下最少的硬币个数。
2.确定递推公式
特殊情况:如果存在的面值无法满足总金额要求,则将二维数组的值设为最大值(为什么要设为最大值?因为要求的是在满足总金额下硬币最少的情况),然后做判断之后返回-1
如何与完全背包问题相联系:类比思想
总金额 - 类比为背包容量
硬币面值 - 类比为物品重量
硬币个数 - 类比为物品价值,固定为1 (求价值(个数)最小的)
伪代码
if(装得下) {
min(上次价值(个数), 剩余容量能装下的最小价值(个数)+1)
dp[i][j] = min(dp[i-1][j], dp[i][j-item.weight] + 1)
} else {
保留上次价值(个数)不变
dp[i][j] = dp[i-1][j]
}
for (int i=1;i<coins.length;i++){
for (int j = 0; j < amount + 1; j++) {
if (j>coins[i]){
dp[i][j]=Integer.min(dp[i-1][j],dp[i][j-coins[i]]+1);
}
else {
dp[i][j]=dp[i-1][j];
}
//打印调试
print(dp);
}
}3.dp数组初始化
首先第一列的情况下需要的硬币个数恒为0,这个在创建数组时就已经帮我们初始化好了。由于递推公式我们需要将第一行初始化,并且在初始化的时候还要考虑存在的面值无法满足总金额要求的情况,此时我们不取最大整数而取amount+1,理由是:之后做加法时会溢出变成负数,取amount+1的理由:用总金额除最小的硬币面额可以得到最大的硬币个数,然后再加1便可以得到“最大值”,题目中规定了硬币的最小面值为1,因此最大值为amount+1
for (int j=1;j<amount+1;j++){
if (j>=coins[0]){
dp[0][j]=dp[0][j-coins[0]+1];
}
else {
//不取最大int整数的理由:因为之后做加法时会溢出变成负数,取amount+1的理由:用总金额除最小的硬币面额
//可以得到最大的硬币个数,然后再加1便可以得到“最大值”,此处的硬币的最大金额为1,因此最大值为amount+1
dp[0][j]=amount+1;
}
}4.dp数组遍历赋值文章来源:https://www.toymoban.com/news/detail-861525.html
外层循环为硬币面值,内层循环为总金额
具体代码如下,包括优化后的代码
import java.awt.event.WindowListener;
import java.util.Arrays;
import java.util.concurrent.ForkJoinPool;
import java.util.stream.IntStream;
/**
* 零钱兑换 - 动态规划
* @author CSDN编程小猹
* @date 2023/11/07
*/
public class ChangeMakingProblemLeetCode322 {
public static void main(String[] args) {
ChangeMakingProblemLeetCode322 leetcode = new ChangeMakingProblemLeetCode322();
int count = leetcode.coinChange(new int[]{1, 2, 5}, 5);
// int count = leetcode.coinChange(new int[]{25, 10, 5, 1}, 41);
// int count = leetcode.coinChange(new int[]{2}, 3);
// int count = leetcode.coinChange(new int[]{15, 10, 1}, 21);
System.out.println(count);
}
private int coinChange(int[] coins, int amount) {
int[][] dp=new int[coins.length][amount+1];
//第一行初始化
for (int j=1;j<amount+1;j++){
if (j>=coins[0]){
dp[0][j]=dp[0][j-coins[0]+1];
}
else {
//不取最大int整数的理由:因为之后做加法时会溢出变成负数,取amount+1的理由:用总金额除最小的硬币面额
//可以得到最大的硬币个数,然后再加1便可以得到“最大值”,此处的硬币的最大金额为1,因此最大值为amount+1
dp[0][j]=amount+1;
}
}
for (int i=1;i<coins.length;i++){
for (int j = 0; j < amount + 1; j++) {
if (j>coins[i]){
dp[i][j]=Integer.min(dp[i-1][j],dp[i][j-coins[i]]+1);
}
else {
dp[i][j]=dp[i-1][j];
}
//打印调试
print(dp);
}
}
return dp[coins.length-1][amount]<amount+1?dp[coins.length-1][amount]:-1;
}
//算法优化:数组降维
public int coinChange1(int[] coins, int amount) {
int[] dp = new int[amount + 1];
// 第一行初始化,填充;0 max max max max max
Arrays.fill(dp, amount + 1);
dp[0] = 0;
System.out.println(Arrays.toString(dp));
for (int coin : coins) {
//此处j=coin,直接装得下的情况开始循环,减少时间复杂度
for (int j = coin; j < amount + 1; j++) {
dp[j] = Math.min(dp[j], 1 + dp[j - coin]);
}
System.out.println(Arrays.toString(dp));
}
int r = dp[amount];
return r > amount ? -1 : r;
}
static void print(int[][] dp) {
System.out.println("-".repeat(18));
Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
System.out.printf(("%2d ".repeat(dp[0].length)) + "%n", array);
for (int[] d : dp) {
array = Arrays.stream(d).boxed().toArray();
System.out.printf(("%2d ".repeat(d.length)) + "%n", array);
}
}
}
518.零钱兑换 二

基本步骤:
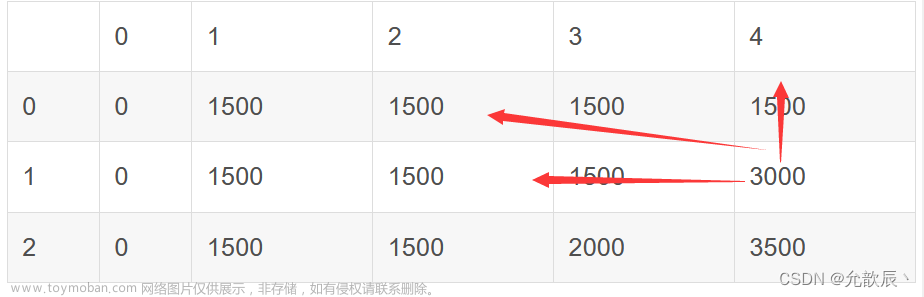
1.确定缓存数组dp和其索引的含义
行(i)代表不同硬币的面额,列(j)代表总金额,二维数组的值dp[i][j]代表着在0-i个不同硬币面值和总金额数为j的情况下凑成金额的凑法。
2.确定递推公式
伪代码
if(放得下):
dp[i][j] = dp[i-1][j] + dp[i][j-coin]
else(放不下)
dp[i][j] = dp[i-1][j]
for (int i = 1; i <coins.length ; i++) {
for (int j = 1; j <amount+1 ; j++) {
if (j>=coins[i]){
dp[i][j]=dp[i-1][j]+dp[i][j-coins[i]];
}
else {
dp[i][j]=dp[i-1][j];
}
}
print(dp);
}3.数组初始化
第零列元素需要全部初始化为1,原因是价值为0的取法只有一个,就是一个coin都不取
由递推式可知第一列元素也需要初始化
//将第零列初始化为1
for (int i = 0; i <coins.length ; i++) {
dp[i][0]=1;
}
//将第零行初始化
for (int j=1;j<amount+1;j++){
if (j>coins[0]){
dp[0][j]=dp[0][j-coins[0]];
}
}4.dp数组遍历赋值
外层循环为硬币面值,内层循环为总金额
import java.util.Arrays;
import java.util.ConcurrentModificationException;
import java.util.stream.IntStream;
/**
*零钱兑换 II - 动态规划
* @author CSDN编程小猹
* @date 2023/11/07
*/
public class ChangeMakingProblemLeetCode518 {
public static void main(String[] args) {
ChangeMakingProblemLeetCode518 leetcode = new ChangeMakingProblemLeetCode518();
// int count = leetcode.change(new int[]{1, 2, 5}, 5);
// int count = leetcode.change(new int[]{2}, 3);
// int count = leetcode.change(new int[]{15, 10, 1}, 21);
int count = leetcode.change(new int[]{25, 10, 5, 1}, 41);
System.out.println(count);
}
private int change(int[] coins, int amount) {
int [][] dp=new int[coins.length][amount+1];
//将第零列初始化为1
for (int i = 0; i <coins.length ; i++) {
dp[i][0]=1;
}
//将第零行初始化
for (int j=1;j<amount+1;j++){
if (j>coins[0]){
dp[0][j]=dp[0][j-coins[0]];
}
}
print(dp);
for (int i = 1; i <coins.length ; i++) {
for (int j = 1; j <amount+1 ; j++) {
if (j>=coins[i]){
dp[i][j]=dp[i-1][j]+dp[i][j-coins[i]];
}
else {
dp[i][j]=dp[i-1][j];
}
}
print(dp);
}
return dp[coins.length-1][amount];
}
//算法优化:数组降维
private int change2(int[] coins, int amount) {
int [] dp=new int[amount+1];
//将第零列初始化为1
dp[0]=1;
//将第零行初始化
for (int j=1;j<amount+1;j++){
if (j>coins[0]){
dp[j]=dp[j-coins[0]];
}
}
System.out.println(Arrays.toString(dp));
for (int i = 1; i <coins.length ; i++) {
for (int j = 1; j <amount+1 ; j++) {
if (j>=coins[i]){
dp[j]=dp[j]+dp[j-coins[i]];
}
}
System.out.println(Arrays.toString(dp));
}
return dp[amount];
}
static void print(int[][] dp) {
System.out.println("-".repeat(18));
Object[] array = IntStream.range(0, dp[0].length + 1).boxed().toArray();
System.out.printf(("%2d ".repeat(dp[0].length)) + "%n", array);
for (int[] d : dp) {
array = Arrays.stream(d).boxed().toArray();
System.out.printf(("%2d ".repeat(d.length)) + "%n", array);
}
}
}
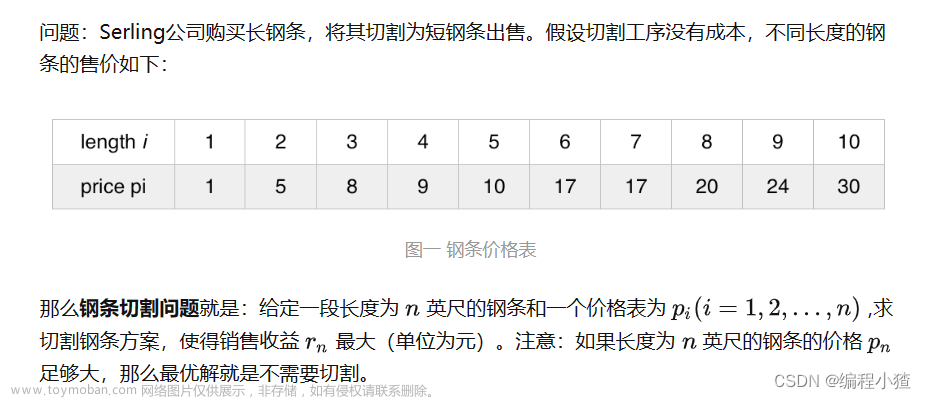
钢条切割问题
基本步骤
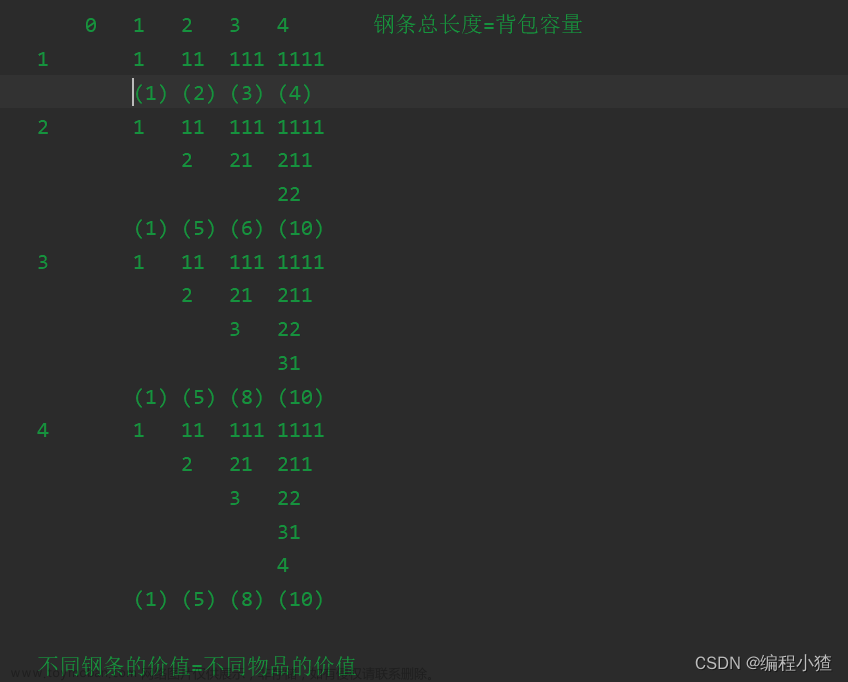
1.确定缓存数组dp和其索引的含义
行(i)代表不同长度钢条的价格,列(j)代表钢条总长度,二维数组的值dp[i][j]代表着在0-i个不同钢条价格和总长度为j的情况下的最大收益。
2.确定递推公式
伪代码:
if(放得下)
dp[i][j]=max(dp[i-1][j],当前物品价值+dp[i][j-物品重量]
else(放不下)
dp[i][j]=dp[i-1][j]
3.dp数组初始化
第零列表示被切割的钢条长度为0,因此其对应的价值一定为0,故第零列初始化为0,在创建数组时已经帮我们初始化好了。第零行表示只有零长度的钢条,那么被切割的钢条无论是多少其对应价值都为0。这个也是在创建数组时已经帮我们初始化好了,不需要我们再格外初始化。
4.dp数组遍历赋值
外层循环为不同钢条的价值,内层循环为被切割的总长度文章来源地址https://www.toymoban.com/news/detail-861525.html
/**
* 钢条切割问题 - 动态规划
* @author CSDN编程小猹
* @date 2023/11/09
*/
public class CutRodProblem {
static int cut(int [] values,int n){
int [][]dp=new int[values.length][n+1];
for (int i = 1; i <values.length ; i++) {
for (int j = 1; j <n+1 ; j++) {
if (j>i){
dp[i][j]=dp[i-1][j];
}
else {
dp[i][j]=Integer.max(dp[i-1][j],values[i]+dp[i][j-1]);
}
}
}
return dp[values.length-1][n];
}
public static void main(String[] args) {
// 不同长度钢条的价值数组,数组的索引对应钢条的长度(物品重量)
System.out.println(cut(new int[]{0, 1, 5, 8, 9,}, 4)); // 10, 17, 17, 20, 24, 30
}
}
到了这里,关于动态规划-背包问题(java版)的文章就介绍完了。如果您还想了解更多内容,请在右上角搜索TOY模板网以前的文章或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!