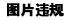探究浮点数精度问题:为何 0.1 + 0.2 不等于 0.3
浮点数精度问题
在很多编程语言中,我们都会发现一个奇怪的现象,就是计算 0.1 + 0.2,它得到的结果并不是 0.3,比如 C、C++、JavaScript 、Python、Java、Ruby 等,都会有这个问题。
为此,有人还做出了一个 https://0.30000000000000004.com/ 网站,在这个网站上我们可以找到哪些编程语言在计算 0.1 + 0.2 的结果并不是 0.3,而是 0.30000000000000004。
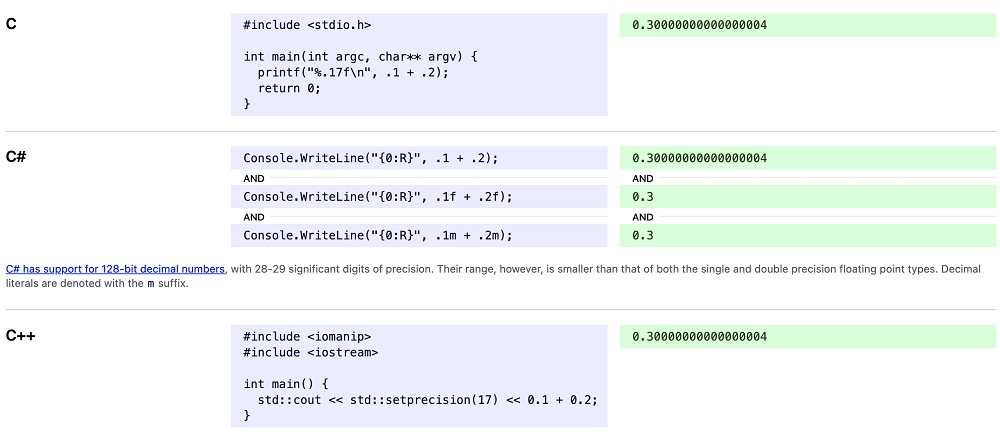

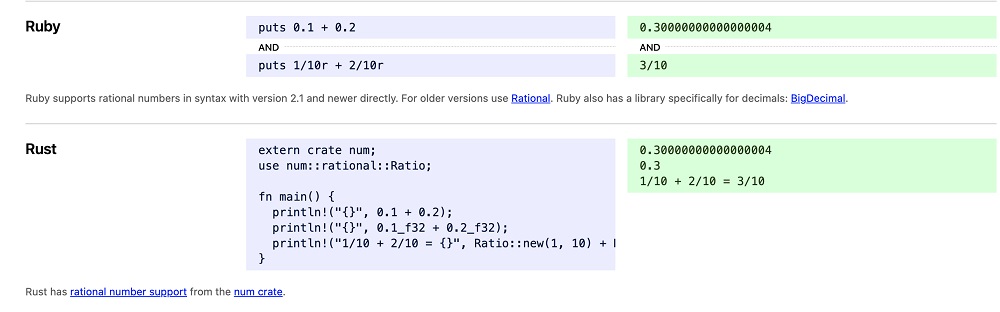

我们可以用 JavaScript 来做演示,计算 0.1 + 0.2,它得到的结果并不是0.3,而是 0.30000000000000004。
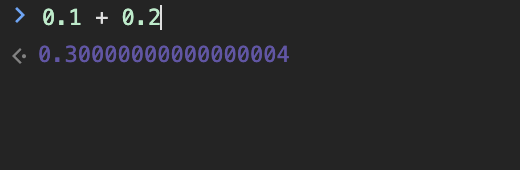
当然如果你把它作为条件判断语句,返回的也是 false:
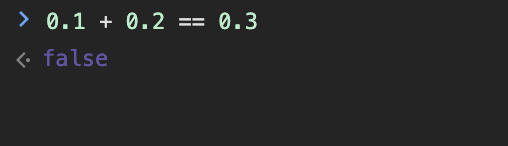
还有其他的例子:
6 * 0.1 = 0.6 但计算机显示为 0.6000000000000001 0.11 + 0.12 = 0.23 但计算机显示为 0.22999999999999998 0.1 + 0.7 = 0.8 但计算机显示为 0.7999999999999999 0.3+0.6 = 0.9 但计算机显示为0.8999999999999999
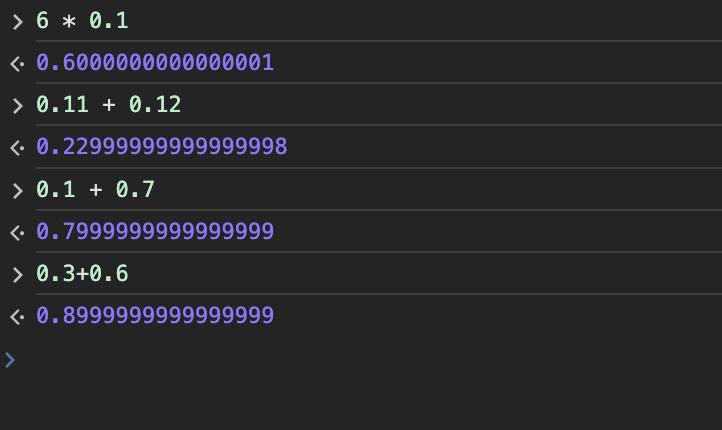
而以下几个计算式却能得到我们想要的结果:
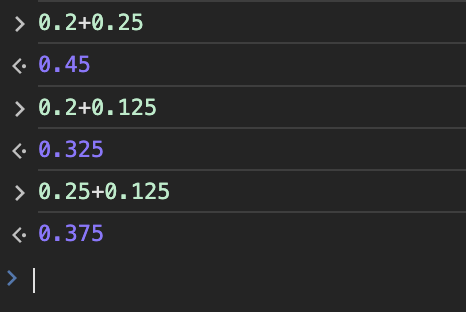
这是为什么?
IEEE 754标准
简单来说,计算机使用基于二进制的浮点数,而我们人类使用基于十进制的浮点数。
背后原理
10 的质因数是 2 和 5。
2 是 2 的唯一质因数。
让我们以 0.1 为例,来理解二进制和十进制的表示:
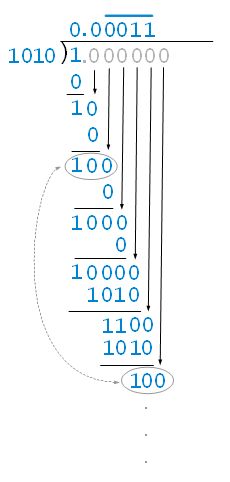
因此,0.1 在二进制中的表示为 0.0001100110011001100110011...(无限循环)。
十进制小数转二进制
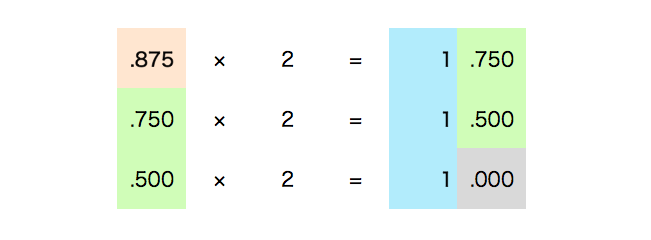
0.1 = 0.0001100110011001100110011001100110011001100110011001101...

十进制小数 0.2 转化为二进制就是:
0.2 = 0.001100110011001100110011001100110011001100110011001101...

解决办法
1、小数先转整数
可以先把小数转换成整数,再相加之后转回小数,如下实例:
(0.1*10 + 0.2*10)/10
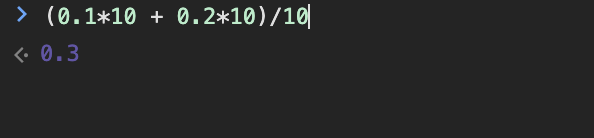
2、使用 toFixed() 方法
let sum = 0.1 + 0.2; console.log(sum.toFixed(2)); // 输出: 0.30
需要注意的是,toFixed()方法虽然在显示上解决了问题,但它并没有改变数字的实际值,它只是改变了数字的表示形式。
3、使用 decimal.js 库
在 JavaScript 中处理浮点数的精度问题时,使用 decimal.js 库是一个更为精确和可靠的解决方案。
decimal.js 是一个任意精度的十进制数学库,它能够避免原生 JavaScript 中浮点数运算的不精确性。
Github 地址:https://github.com/MikeMcl/decimal.js
首先,你需要在你的项目中引入 decimal.js 库。
使用 npm 安装:
npm install decimal.js
在 HTML 中引入:
<script src="https://cdnjs.cloudflare.com/ajax/libs/decimal.js/10.2.0/decimal.min.js"></script>
示例
接下来,你可以使用 decimal.js 来处理浮点数的运算,下面是一个例子:文章来源:https://www.toymoban.com/diary/system/758.html
// 引入Decimal构造函数
const Decimal = decimal. Decimal;
// 创建两个Decimal对象
let a = new Decimal('0.1');
let b = new Decimal('0.2');
// 进行加法运算
let sum = a.plus(b);
// 输出结果
console.log(sum.toString()); // 输出: 0.3使用 decimal.js 库得到的结果是准确的 0.3,而不是原生 JavaScript 中的近似值。文章来源地址https://www.toymoban.com/diary/system/758.html
到此这篇关于0.1+0.2不等于0.3的真相 - 计算机浮点数运算的秘密的文章就介绍到这了,更多相关内容可以在右上角搜索或继续浏览下面的相关文章,希望大家以后多多支持TOY模板网!